Inclusion-exclusion formula

inclusion-exclusion principle, inclusion-exclusion method

The inclusion-exclusion principle is used in many branches of pure and applied mathematics. In probability theory it means the following theorem: Let $A _ { 1 } , \ldots , A _ { n }$ be events in a probability space and

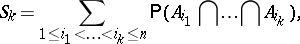(a1)

\begin{equation*} k = 1 , \dots , n. \end{equation*}

Then one has the relation

\begin{equation} \tag{a2} \mathsf{P} ( A _ { 1 } \bigcup \ldots \bigcup A _ { n } ) = S _ { 1 } - S _ { 2 } + \ldots + ( - 1 ) ^ { n - 1 } S _ { n }. \end{equation}

This theorem can easily be proved by induction on $n$. Another proof can be given by the use of indicator variables, as follows. In connection with an event $A$ one defines $I _ { A } = 1$ if $A$ occurs, and $I _ { A } = 0$ otherwise. Then the equation

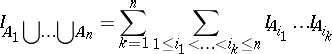(a3)

holds. Taking expectations on both sides, the theorem follows.

If one wants to find the probability of $A _ { 1 } \cap \ldots \cap A _ { n }$, then first one observes that $\mathsf{P} ( A _ { 1 } \cap \ldots \cap A _ { n } ) = 1 - \mathsf{P} ( \overline { A } _ { 1 } \cup \ldots \cup \overline { A } _ { n } )$ and then uses (a2) for the events $\overline { A } _ { 1 } , \dots , \overline { A } _ { n }$.

The theorem is frequently attributed to H. Poincaré [a8]. However, it was already known to A. De Moivre [a2] and the even more general formula for the probability that at least $r$ events occur has been found by r equation','../p/p072950.htm','Positive variation of a function','../p/p073970.htm','Rectifiable curve','../r/r080130.htm','Variation of a function','../v/v096110.htm')" style="background-color:yellow;">C. Jordan [a4]. See also [a5] for further references. All these formulas concern Boolean functions of random events.

An example for the application of formula (a2) is the solution of the classical problem of coincidences proposed by P.R. Montmort [a7]: A box contains $n$ cards marked $1 , \dots , n$ and all cards are drawn, one by one, without replacement, where each sequence has the same probability; one says that a coincidence occurs at the $i$th drawing, or event $A_i$ occurs, if the card drawn is marked $i$; the problem is to find the probability that at least one coincidence occurs (cf. also Montmort matching problem). One easily sees that for any $1 \leq i_{1} < \ldots < i_{k} \leq n$ one has

\begin{equation*} \mathsf{P} ( A _ { i_{1} } \bigcap \ldots \bigcap A _ { i_{k} } ) = \frac { ( n - k ) ! } { n ! }, \end{equation*}

hence

\begin{equation*} S _ { k } = \left( \begin{array} { c } { n } \\ { k } \end{array} \right) \frac { ( n - k ) ! } { n ! } \end{equation*}

and

\begin{equation*} \mathsf{P} ( A _ { 1 } \bigcap \ldots \bigcap A _ { n } ) = \sum _ { k = 1 } ^ { n } ( - 1 ) ^ { k - 1 } \frac { 1 } { k ! }. \end{equation*}

The numbers $S _ { k }$ have another probabilistic interpretation: $S _ { k } = \mathsf{E} \left[ \left( \begin{array} { l } { X } \\ { k } \end{array} \right) \right]$, where $X = I _ { A _ { 1 } } + \ldots + I _ { A _ { n } }$, i.e., $X$ is the number of events which occur. One says that $S _ { k }$ is the $k$th binomial moment of $X$. For a proof of the above equation, see, e.g., [a11].

There are many practical applications where one needs to compute the probability of a union, or other Boolean function of events. Prominent are those in reliability theory. For example, in a communication network, where the links randomly work or fail, one may want to find a two-terminal reliability or the all-terminal reliability. In the former case one has to find the probability that all links in at least one path connecting the two terminal nodes work, and in the latter case the probability that all links in at least one spanning tree work. In both cases the number of random events is too large to apply inclusion-exclusion. In fact, one may be able to compute only a few of the binomial moments involved. In such cases one looks for bounds. The simplest ones, for the probability of the union, are the Bonferroni bounds:

\begin{equation*} \mathsf{P} ( A _ { 1 } \bigcup \ldots \bigcup A _ { n } ) \geq S _ { 1 } - S _ { 2 } + \ldots + S _ { m - 1 } - S _ { m } \end{equation*}

if $m$ is even, and

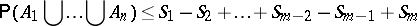if $m$ is odd, where $m < n$ (cf. also Bonferroni inequalities). However, in many cases these bounds are not sufficiently tight.

A general, efficient method for bounding $\mathsf{P} ( A _ { 1 } \cup \ldots \cup A _ { n } )$ and other Boolean functions of events has been worked out by A. Prékopa (see [a10] and the references therein). In the case of bounding the probability of the union one observes that $S _ { k } = \mathsf{E} \left[ \left( \begin{array} { l } { X } \\ { k } \end{array} \right) \right] = \sum _ { i = 1 } ^ { n } \left( \begin{array} { l } { i } \\ { k } \end{array} \right) p_{i}$, where $p _ { i }$ is the probability that exactly $i$ events occur. Then, if one knows $S _ { 1 } , \ldots , S _ { m }$, where $m < n$, but the $p_{i}$ are unknown, one solves the linear programs:

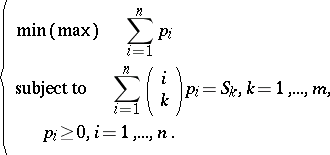(a4)

If 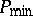and $P _ { \text { max } }$ are the optimum values corresponding to the min and max problems, respectively, then these are sharp bounds for the probability of the union, i.e.

\begin{equation*} P _ { \operatorname { min } } \leq \mathsf{P} ( A _ { 1 } \bigcup \dots \bigcup A _ { n } ) \leq P _ { \text{max} } \end{equation*}

and no better bounds can be given based on the knowledge of $S _ { 1 } , \ldots , S _ { m }$. There are simple and efficient algorithms to solve problems (a4) which are variants of the dual algorithm of linear programming. The sharp bounding formulas can also be written as

\begin{equation*} \sum _ { k = 1 } ^ { m } x _ { k } S _ { k } \leq \mathsf{P} ( A _ { 1 } \bigcup \ldots \bigcup A _ { n } ) \leq \sum _ { k = 1 } ^ { m } y _ { k } S _ { k }, \end{equation*}

where $\mathbf x = ( x _ { 1 } , \dots , x _ { m } ) ^ { T }$ and $\mathbf{y} = ( y _ { 1 } , \dots , y _ { m } ) ^ { T }$ are optimal solutions of the duals of the min and max problems, respectively. It has been shown that the components of $\mathbf{x}$ and $\mathbf{y}$ have alternating signs, starting with $+$, and $| x _ { 1 } | \geq \ldots \geq | x _ { m } |$, $| y _ { 1 } | \geq \ldots \geq | y _ { m } |$. The optimum values can be expressed by formulas if $m \leq 4$ (see the references in [a10]).

Formula (a2) holds for any finitely additive set function $\mu$ defined on an algebra $\mathcal{S}$ of some subsets of $\Omega$ (if $A \in \mathcal S$, then $\overline{A} \in \mathcal{S}$, and if $A , B \in \mathcal S$, then $A \cup B \in \mathcal{S}$). In particular, one may take $\Omega$ an arbitrary finite set, $\mathcal{S}$ all subsets of $\Omega$ and $\mu ( A ) = | A |$, the cardinality of the set $A$. The latter case has many applications in combinatorics, especially in enumeration problems. A good sample of combinatorial problems, where inclusion-exclusion is used, is presented in [a6].

Inclusion-exclusion plays also an important role in number theory. Here one calls it the sieve formula or sieve method. In this respect, V. Brun did pioneering work [a1] (cf. also Sieve method; Brun sieve). For a summary of the sieve methods, see [a9] and [a3]. A simple but revealing example is the formula for $\varphi ( n )$, the number of those positive integers that are relative prime to, and smaller than, $n$. If $n$ has prime divisors $p _ { 1 } , \dots , p _ { k }$, then the inclusion-exclusion principle gives:

\begin{equation*} \varphi ( n ) = n - \frac { n } { p _ { 1 } } - \ldots - \frac { n } { p _ { k } } + \end{equation*}

\begin{equation*} + \frac { n } { p _ { 1 } p _ { 2 } } + \ldots + \frac { n } { p _ { k - 1 } p _ { k } } + - \frac { n } { p _ { 1 } p _ { 2 } p _ { 3 } } - \ldots + ( - 1 ) ^ { k } \frac { n } { p _ { 1 } \ldots p _ { k } }. \end{equation*}

References

[a1]	V. Brun, "Le crible d'Eratosthène et le théorème de Goldbach" Skrifter Norske Vid.-Akad. Kristiana I , 3 (1920)
[a2]	A. De Moivre, "Doctrine of chances" , London (1718)
[a3]	H. Halberstam, H.E. Richert, "Sieve methods" , Acad. Press (1974)
[a4]	C. Jordan, "De quelques formules de probabilité" C.R. Acad. Sci. Paris , 65 (1867) pp. 993–994
[a5]	K. Jordan, "Chapters on the classical calculus of probability" , Akad. Kiadó (1972)
[a6]	L. Lovász, "Combinatorial problems and exercises" , Akad. Kiadó (1993)
[a7]	P.R. Montmort, "Essai d'analyse sur les jeux de hazard" , Paris (1708)
[a8]	H. Poincaré, "Calcul des probabilités" , Gauthier-Villars (1896)
[a9]	K. Prachar, "Primzahlverteilung" , Springer (1957)
[a10]	A. Prékopa, "Stochastic programming" , Kluwer Acad. Publ. (1995)
[a11]	L. Takács, "On the method of inclusion and exclusion" J. Amer. Statist. Assoc. , 62 (1967) pp. 102–113