Markov braid theorem

If two closed braids represent the same ambient isotopy class of oriented links (cf. also Braid theory), then one can transform one braid to another by a sequence of Markov moves:

i) $a \leftrightarrow b a b ^ { - 1 }$ (conjugation).

ii) $a \leftrightarrow a b ^ { \pm 1 }_ { n }$, where $a$ is an element of the $n$th braid group

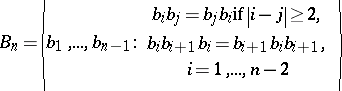and $b _ { n }$ is the $n$th generator of the $( n + 1 )$th braid group.

Markov's braid theorem is an important ingredient in the construction of the Jones polynomial and its generalizations (e.g. the Jones–Conway polynomial).

References

[a1]	J.S. Birman, "Braids, links and mapping class groups" , Ann. of Math. Stud. , 82 , Princeton Univ. Press (1974)
[a2]	A.A. Markov, "Über die freie Aquivalenz der geschlossen Zopfe" Recueil Math. Moscou , 1 (1935) pp. 73–78
[a3]	N.M. Weinberg, "On free equivalence of free braids" C.R. (Dokl.) Acad. Sci. USSR , 23 (1939) pp. 215–216 (In Russian)