Seifert matrix
A matrix associated with knots and links in order to investigate their topological properties by algebraic methods (cf. Knot theory). Named after H. Seifert [1], who applied the construction to obtain algebraic invariants of one-dimensional knots in 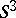 . Let
. Let 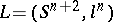 be an
be an  -dimensional
-dimensional 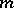 -component link, i.e. a pair consisting of an oriented sphere
-component link, i.e. a pair consisting of an oriented sphere 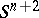 and a differentiable or piecewise-linear oriented submanifold
and a differentiable or piecewise-linear oriented submanifold 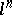 of this sphere which is homeomorphic to the disconnected union of
of this sphere which is homeomorphic to the disconnected union of 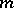 copies of the sphere
copies of the sphere 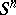 . There exists a compact
. There exists a compact 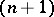 -dimensional orientable submanifold
-dimensional orientable submanifold 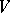 of
of 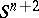 such that
such that 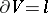 ; it is known as the Seifert manifold of the link
; it is known as the Seifert manifold of the link 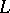 . The orientation of the Seifert manifold
. The orientation of the Seifert manifold 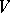 is determined by the orientation of its boundary
is determined by the orientation of its boundary 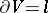 ; since the orientation of
; since the orientation of 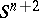 is fixed, the normal bundle to
is fixed, the normal bundle to 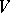 in
in 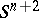 turns out to be oriented, so that one can speak of the field of positive normals to
turns out to be oriented, so that one can speak of the field of positive normals to 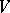 . Let
. Let 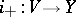 be a small displacement along this field, where
be a small displacement along this field, where 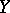 is the complement to an open tubular neighbourhood of
is the complement to an open tubular neighbourhood of 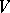 in
in 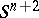 . If
. If 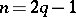 is odd, one defines a pairing
is odd, one defines a pairing
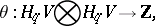 |
associating with an element 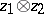 the linking coefficient of the classes
the linking coefficient of the classes 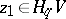 and
and 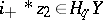 . This
. This 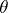 is known as the Seifert pairing of the link
is known as the Seifert pairing of the link 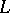 . If
. If 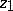 and
and 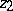 are of finite order, then
are of finite order, then 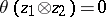 . The following formula is valid:
. The following formula is valid:
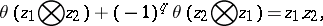 |
where the right-hand side is the intersection index (in homology) of the classes 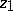 and
and 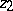 on
on 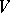 .
.
Let  be a basis for the free part of the group
be a basis for the free part of the group 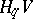 . The
. The 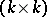 -matrix
-matrix 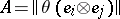 with integer entries is called the Seifert matrix of
with integer entries is called the Seifert matrix of 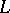 . The Seifert matrix of any
. The Seifert matrix of any 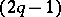 -dimensional knot has the following property: The matrix
-dimensional knot has the following property: The matrix 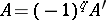 is unimodular (cf. Unimodular matrix), and for
is unimodular (cf. Unimodular matrix), and for 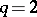 the signature of the matrix
the signature of the matrix 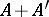 is divisible by
is divisible by 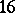 (
(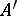 is the transpose of
is the transpose of 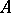 ). Any square matrix
). Any square matrix 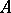 with integer entries is the Seifert matrix of some
with integer entries is the Seifert matrix of some 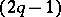 -dimensional knot if
-dimensional knot if 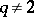 , and the matrix
, and the matrix 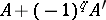 is unimodular.
is unimodular.
The Seifert matrix itself is not an invariant of the link 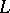 ; the reason is that the construction of the Seifert manifold
; the reason is that the construction of the Seifert manifold 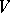 and the choice of the basis
and the choice of the basis  are not unique. Matrices of the form
are not unique. Matrices of the form
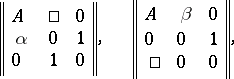 |
where 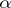 is a row-vector and
is a row-vector and 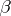 a column-vector, are known as elementary expansions of
a column-vector, are known as elementary expansions of 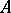 , while
, while 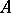 itself is called an elementary reduction of its elementary expansions. Two square matrices are said to be
itself is called an elementary reduction of its elementary expansions. Two square matrices are said to be 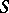 -equivalent if one can be derived from the other via elementary reductions, elementary expansions and unimodular congruences (i.e. transformations
-equivalent if one can be derived from the other via elementary reductions, elementary expansions and unimodular congruences (i.e. transformations 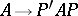 , where
, where 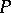 is a unimodular matrix). For higher-dimensional knots
is a unimodular matrix). For higher-dimensional knots 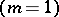 and one-dimensional links
and one-dimensional links 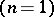 the
the 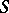 -equivalence class of the Seifert matrix is an invariant of the type of the link
-equivalence class of the Seifert matrix is an invariant of the type of the link 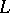 . In case
. In case 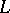 is a knot, the Seifert matrix
is a knot, the Seifert matrix 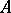 uniquely determines a
uniquely determines a 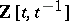 -module
-module 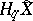 , where
, where 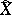 is an infinite cyclic covering of the complement of the knot. The polynomial matrix
is an infinite cyclic covering of the complement of the knot. The polynomial matrix 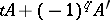 is the Alexander matrix (see Alexander invariants) of the module
is the Alexander matrix (see Alexander invariants) of the module 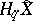 . The Seifert matrix also determines the
. The Seifert matrix also determines the 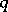 -dimensional homology and the linking coefficients in the cyclic coverings of the sphere
-dimensional homology and the linking coefficients in the cyclic coverings of the sphere 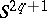 that ramify over the link.
that ramify over the link.
References
| [1] | H. Seifert, "Ueber das Geschlecht von Knoten" Math. Ann. , 110 (1934) pp. 571–592 |
| [2] | R.H. Crowell, R.H. Fox, "Introduction to knot theory" , Ginn (1963) |
| [3] | J. Levine, "Polynomial invariants of knots of codimension two" Ann. of Math. , 84 (1966) pp. 537–554 |
| [4] | J. Levine, "An algebraic classification of some knots of codimension two" Comment. Math. Helv. , 45 (1970) pp. 185–198 |
Comments
For a description of the Seifert manifold in the case 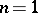 , i.e. the Seifert surface of a link, cf. Knot and link diagrams.
, i.e. the Seifert surface of a link, cf. Knot and link diagrams.
Seifert matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Seifert_matrix&oldid=48646