Kerdock and Preparata codes
A most famous relation in coding theory is a discrete avatar of the Fourier transform which relates the weight enumerator $ W _ {C} $
of a linear code $ C $
and the weight enumerator of its dual $ C ^ \perp $
with respect to the standard scalar product, namely
$$ W _ {C ^ \perp } ( x,y ) = { \frac{1}{\left | C \right | } } W _ {C} ( x + y,x - y ) . $$
(Cf. MacWilliams identities.) A simple example of a dual pair of codes is the Hamming code $ H _ {m} $, a (big) $ [ n = 2 ^ {m} ,n - m - 1,4 ] $ code whose dual is the (small) first-order Reed–Muller code $ R _ {m} $. The matrix
$$ \left ( \begin{array}{ccccccc} 1 & 1 & 1 & 1 & 1 &\dots & 1 \\ 0 & 1 &\alpha &\alpha ^ {2} &\alpha ^ {3} &\dots &\alpha ^ {n - 1 } \\ \end{array} \right ) , $$
where $ n = 2 ^ {m} - 1 $ and $ \alpha $ is a root of $ {\overline{f}\; } ( x ) $, is both a generator matrix for $ R _ {m} $ and a parity check matrix for $ H _ {m} $. The small code $ R _ {m} $ has the simple weight distribution
$$ W _ {R _ {m} } ( x,y ) = x ^ {n} + y ^ {n} + ( 2n - 2 ) ( xy ) ^ {n/2 } . $$
The MacWilliams formula now gives an explicit expression for $ W _ {H _ {m} } $ which would be cumbersome to obtain directly.
There is no Fourier transform without Abelian groups and therefore there is no MacWilliams formula for non-linear codes. The discovery first of the $ ( 16,256,6 ) $[[ Nordstrom–Robinson code]] in 1967, non-linear and still formally self-dual for the MacWilliams relation, followed in 1968 and 1972 [a8] by the discovery of two infinite families of non-linear codes, the Preparata codes and Kerdock codes, respectively, whose weight enumerators are MacWilliams dual of each other, were until [a4] an unexplained phenomenon. The unsuccessful efforts of many distinguished researchers on this notoriously difficult problem [a8] led one of them to declare [a5] that it was "merely a coincidence" .
A well-known trick in modulation theory to address the $ 4 $- PSK constellation consists of using a (very simple) case of the Gray mapping. This is a mapping from $ \mathbf Z _ {4} $ to $ { \mathop{\rm GF} } ( 2 ) ^ {2} $ defined by
$$ 0 \rightarrow 00, 1 \rightarrow 01, 2 \rightarrow 11, 3 \rightarrow 10, $$
and extended to a mapping from $ \mathbf Z _ {4} ^ {n} $ to $ { \mathop{\rm GF} } ( 2 ) ^ {2n } $ in the natural way. The key property is that the mapping $ \phi $ from $ \mathbf Z _ {4} ^ {n} $ equipped with the Lee distance to $ { \mathop{\rm GF} } ( 2 ) ^ {2n } $ equipped with the Hamming distance is an isometric mapping of metric spaces. The trace parametrization of quaternary $ M $- sequences can be used to show that the Kerdock code as defined in [a8], p. 1107, is essentially the cyclic code associated to construction $ A $ of [a1], p. 458, and the construction of [a9]. In particular, if $ \xi $ denotes a primitive root of $ n $ in a suitable Galois ring, [a7], then the matrix
$$ \left ( \begin{array}{ccccccc} 1 & 1 & 1 & 1 & 1 &\dots & 1 \\ 0 & 1 &\xi &\xi ^ {2} &\xi ^ {3} &\dots &\xi ^ {n - 1 } \\ \end{array} \right ) $$
( $ n = 2 ^ {m} - 1 $, with $ m \geq 3 $ odd) is both a generator matrix for the Kerdock code and a parity check matrix for the "Preparata" code. One sees that the Kerdock and Preparata codes are quaternary analogues of the first-order Reed–Muller code and of the extended Hamming code, respectively. The Goethals and Delsarte–Goethals codes, which are also a quaternary dual pair, are related in a less simple manner to three error-correcting BCH codes.
Besides MacWilliams duality, the $ \mathbf Z _ {4} $ structure also bears influence on the decoding (cf. [a4], Fig. 2) and on the coset structure of the Preparata code, which gives rise to a new distance-regular graph of diameter $ 4 $[a4].
The article [a4], which solves a twenty-year-old riddle, was awarded the 1995 IEEE Information Theory award for best paper. Geometrical repercussions can be found in [a3], [a6].
References
| [a1] | S. Boztas, A.R. Hammons, P. V. Kumar, "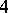 -phase sequence with near optimum correlation properties" IEEE Trans. Inform. Th. , 38 (1992) pp. 1101–1113 -phase sequence with near optimum correlation properties" IEEE Trans. Inform. Th. , 38 (1992) pp. 1101–1113 |
| [a2] | J.H. Conway, N.J.A. Sloane, "Sphere packings, lattices and groups" , Springer (1992) |
| [a3] | A.R. Calderbank, P.J. Cameron, W.M. Kantor, J.J. Seidel, "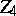 -Kerdock codes, orthogonal spreads, and extremal euclidean line sets" Proc. London Math. Soc. (to appear) -Kerdock codes, orthogonal spreads, and extremal euclidean line sets" Proc. London Math. Soc. (to appear) |
| [a4] | A.R. Hammons, P.V. Kumar, A.R. Calderbank, N.J.A. Sloane, P. Solé, "The 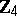 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 |
| [a5] | W.M. Kantor, "On the inequivalence of generalized Preparata codes" IEEE Inform. Th. , 29 (1983) pp. 345–348 |
| [a6] | W.M. Kantor, "Quaternionic line sets and quaternionic Kerdock codes" Linear Alg. & Its Appl. (special issue in honor of J.J. Seidel) , 226–228 (1995) pp. 749–779 |
| [a7] | B.R. MacDonald, "Finite rings with identity" , M. Dekker (1974) |
| [a8] | F.J. MacWilliams, N.J.A. Sloane, "The theory of error-correcting codes" , North-Holland (1977) |
| [a9] | P. Solé, "A quaternary cyclic code and a family of quaternary sequences with low correlation" , Lecture Notes in Computer Science , 388 , Springer (1989) pp. 193–201 |
Kerdock and Preparata codes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kerdock_and_Preparata_codes&oldid=38583