Lambda-ring

A pre-$\lambda$-ring is a commutative ring $R$ with identity element $1$ and a set of mappings $\lambda^n : R \rightarrow R$, $n = 0,1,2,\ldots$ such that

i) $\lambda^0(x) = 1$ for all $x \in R$;

ii) $\lambda^1(x) = x$ for all $x \in R$;

iii) $\lambda^n(x+y) = \sum_{i+j=n} \lambda^i(x) \lambda^j(y)$.

Examples are, for instance, the topological $K$-groups $K(M)$ and $K_G(M)$, $G$ a compact Lie group (cf. $K$-theory), and the complex representation ring $R(G)$ of a finite group $G$ (cf. Representation of a compact group). In all these cases the $\lambda^n$ are induced by taking exterior powers. For instance, for $M = \text{pt}$, $K(M) = \mathbf{Z}$ and the $\lambda$-structure is given by $\lambda^n(m) = \binom{m}{n}$ (binomial coefficients; the formula $\binom{m_1+m_2}{n} = \sum_{i+j=n} \binom{m_1}{i} \binom{m_2}{j}$ follows by the binomial expansion theorem from $(X+Y)^{m_1+m_2} = (X+Y)^{m_1} (X+Y)^{m_2}$.

Let $R$ be any commutative ring with unit element 1. Consider the set $\Lambda(R) = 1 + t R[[t]]$ of power series in $t$ over $R$ with constant term 1. Multiplication of power series turns $\Lambda(R)$ into an Abelian group. A pre-$\lambda$-ring structure on $\Lambda(R)$ defines a homomorphism of Abelian groups $\lambda_t : R \rightarrow \Lambda(R)$, $\lambda_t(x) = \lambda^0(x) + \lambda^1(x) t + \lambda^2(x) t^2 + \cdots$, and vice versa.

Let $\alpha(t) = 1 + a_1 t + a_2 t^2 + \cdots$, $\beta(t) = 1 + b_1 t + b_2 t^2 + \cdots$ be two elements of $\Lambda(R)$. Formally, write $$ \alpha(t) = \prod_{i=1}^\infty \left({ 1 - \xi_i t }\right) $$ $$ \beta(t) = \prod_{i=1}^\infty \left({ 1 - \eta_i t }\right) $$ and consider the expressions $$ \prod_{i,j=1}^\infty \left({ 1 - \xi_i \eta_j t }\right) = 1 + P_1 t + P_2 t^2 + \cdots \ , $$ $$ \prod_{i_1 < i_2 < \cdots < i_n}^\infty \left({ 1 - \xi_{i_1} \xi_{i_2} \cdots \xi_{i_n} t }\right) = 1 + L_{1,n} t + L_{2,n} t^2 + \cdots \ . $$

The $P_i$ and $L_{i,n}$ are symmetric polynomial expressions in the $\xi$'s and $\eta$'s and hence can be written as universal polynomial expressions in the $a$'s and $b$'s. Now define a multiplication on $\Lambda(R)$ by $$ \alpha(t) * \beta(t) = 1 + P_1(a,b) t + P_2(a,b) t^2 + \cdots $$ ($a = (a_1,a_2,\ldots)$, $b = (b_1,b_2,\ldots)$), and define operations (mappings) $\lambda^n : \Lambda(R) \rightarrow \Lambda(R)$ by $$ \lambda^n \alpha(t) = 1 + L_{1,n}(a,b) t + L_{2,n}(a,b) t^2 + \cdots \ . $$

The ring $\Lambda(R)$ with these operations is a pre-$\lambda$-ring. Given two pre-$\lambda$-rings $R_1$, $R_2$, a $\lambda$-ring homomorphism $\phi : R_1 \rightarrow R_2$ is a homomorphism of rings such that $\phi(\lambda^n(x)) = \lambda^n(\phi(x))$ for all $x \in R_1$, $n = 0,1,2,\ldots$.

A pre-$\lambda$-ring $R$ is a $\lambda$-ring if $\lambda_{-t} : R \rightarrow \Lambda(R)$, $\lambda_{-t}(x) = 1 - \lambda^1(x) t + \lambda^2(x) t^2 - \cdots$, is a homomorphism of pre-$\lambda$-rings. The ring $\Lambda(R)$ is always a $\lambda$-ring and so are the standard examples $K(M)$, $K_G(M)$, $R(G)$ of pre-$\lambda$-rings mentioned above.

On the other hand, consider a finite group $G$. A finite $G$-set is a finite set together with a group action of $G$. Using disjoint union and Cartesian products with diagonal action, the isomorphism classes of finite $G$-sets form a semi-ring, $A^+(G)$. The associated Grothendieck ring $A(G)$ is called the Burnside ring. On $A^+(G)$, define operations $\lambda^n : A^+(G) \rightarrow A^+(G)$ by taking $\lambda^n(S)$ to be the set of$n$-element subsets of $S$ with the natural induced $G$-action. This generalizes the $\lambda$-operations $\lambda^n$ on $\mathbf{N} \subset \mathbf{Z}$, $\lambda^n(m) = \binom{m}{n}$. Using iii), the $\lambda^n$ extend to $A(G)$, making the Burnside ring into a pre-$\lambda$-ring. As a rule this pre-$\lambda$-ring is not a $\lambda$-ring, [a9].

Instead of pre-$\lambda$-ring and $\lambda$-ring one also finds, respectively, the phrases $\lambda$-ring and special $\lambda$-ring in the literature.

Let $R$ be a pre-$\lambda$-ring. One defines new operations $\psi^i : R \rightarrow R$ by the formula $$ -t \frac{d}{dt} \log \lambda_{-t} (x) = \sum_{i=1}^\infty \psi^i(x) t^i \ . $$

These operations are called the Adams operations on the pre-$\lambda$-ring $R$. They were introduced in the case $R = K(M)$ by J.F. Adams ([a10]).

The Adams operations satisfy

iv) $\Psi^1(x) = x$;

v) $\Psi^n(x+y) = \Psi^n(x) + \Psi^n(y)$.

Let $R$ be a torsion-free pre-$\lambda$-ring; then $R$ is a $\lambda$-ring if and only if the Adams operations satisfy in addition

vi) $\Psi^i(1) = 1$;

vii) $\Psi^n(xy) = \Psi^n(x) \Psi^n(y)$;

viii) $\Psi^{ij}(x) = \Psi^i(\Psi^j(x))$.

A ring $R$ with operations $\Psi^i$ satisfying iv)–viii) is sometimes called a $\Psi$-ring.

The ring $\Lambda(R)$ is isomorphic to the ring $W(R)$ of (big) Witt vectors (cf. (the editorial comments to) Witt vector): $$ \bar E : W(R) \rightarrow \Lambda(R) $$ $$ (a_1,a_2,\ldots) \mapsto \prod_{i=1}^\infty \left({ 1 - a_i t^i }\right) $$

Under this isomorphism the Adams operations $\Psi^n$ on $\Lambda(R)$ correspond to the Frobenius operations $\mathbf{f}_n : W(R) \rightarrow W(R)$.

The $\lambda$-structures on the rings 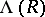define a functorial morphism of ring-valued functors 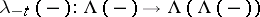. Together with 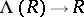, , 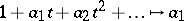this defines a co-triple structure on the functor 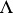, and the 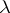-rings are precisely the co-algebras of this co-triple (cf. Triple).

Via the isomorphism 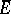one finds "exponential homomorphisms"

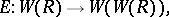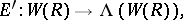which should be seen as (generalizing) the so-called Artin–Hasse exponential ([a11], [a12]).

Let 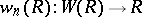be the ring homomorphism

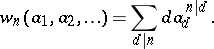Then the Artin–Hasse exponential 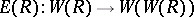is functorially characterized by

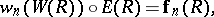where 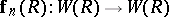is the Frobenius homomorphism.

Let 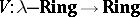be the forgetful functor. Then the functor 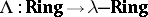is right adjoint (cf. Adjoint functor) to :

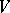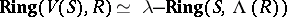(cf. [a5], p. 20).

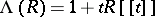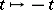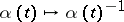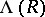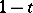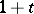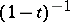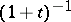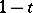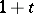There are (besides the identity) three natural automorphisms of the Abelian group , given by the substitution , the "inversion" , and the combination of the two. Correspondingly there are four natural ways to introduce a ring structure on ; the corresponding unit elements are , , , . All four occur in the literature. The most frequently occurring have or as their unit element — here, in the above, 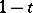is the unit element —, and 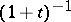seems to be the most rare case.

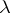-rings were introduced by A. Grothendieck in an algebraic-geometric setting [a2] and were first used in group representation theory by M.F. Atiyah and D.O. Tall ([a1]).

In case 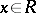is one-dimensional, i.e. 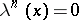for 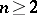, the terminology derives from the case 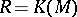or 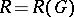; one has 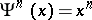, whence the name power operations for the 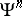. On the 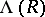the operations 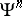are directly defined by

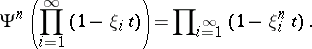References

[a1]	M.F. Atiyah, D.O. Tall, "Group representations, $\lambda$-rings and the $J$-homomorphism" Topology , 8 (1969) pp. 253–297 MR244387
[a2]	A. Grothendieck, "La théorie des classes de Chern" Bull. Soc. Math. France , 86 (1958) pp. 137–154 MR0116023 Zbl 0091.33201
[a3]	A. Grothendieck, "Classes de faisceaux et théorème de Riemann–Roch" , Sem. Géom. Algébrique , 6 , Springer (1972) pp. 20–77 Zbl 0229.14008
[a4]	M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) pp. 144ff MR0506881 MR0463184 Zbl 0454.14020
[a5]	D. Knutson, "$\lambda$-rings and the representation theory of the symmetric group" , Springer (1974) MR0364425 Zbl 0272.20008
[a6]	P. Berthelot, "Généralités sur les $\lambda$-anneaux" , Sem. Géom. Algébrique , 6 , Springer (1972) pp. 297–365
[a7]	W. Fulton, S. Lang, "Riemann–Roch algebra" , Springer (1985) MR0801033 Zbl 0579.14011
[a8]	T. tom Dieck, "Transformation groups and representation theory" , Springer (1979) Zbl 0445.57023
[a9]	C. Siebeneicher, "$\lambda$-Ringstrukturen auf dem Burnsidering der Permutationsdarstellungen einer endlichen Gruppe" Math. Z. , 146 (1976) pp. 223–238 MR0390035 Zbl 0306.20011
[a10]	J.F. Adams, "Vectorfields on spheres" Ann. of Math. , 75 (1962) pp. 603–632 DOI 10.2307/1970213 Zbl 0112.38102
[a11]	M. Hazewinkel, "Twisted Lubin–Tate formal group laws, ramified Witt vectors and (ramified) Artin–Hasse exponentials" Trans. Amer. Math. Soc. , 259 (1980) pp. 47–63 MR0561822 Zbl 0437.13014
[a12]	E. Artin, H. Hasse, "Die beide Ergänzungssätze zum Reciprozitätsgesetz der $\ell^n$-ten Potenzreste im Körper der $\ell^n$-ten Einheitswurzeln" Abh. Math. Sem. Univ. Hamburg , 6 (1928) pp. 146–162
[a13]	G. Whaples, "Generalized local class field theory III: Second form of the existence theorem, structure of analytic groups" Duke Math. J. , 21 (1954) pp. 575–581 MR73645