Conjugate elements
in a group $G$
Elements 
and 
of 
for which
 |
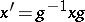for some 
in 
. One also says that 
is the result of conjugating 
by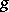 
. The power notation 
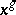is frequently used for the conjugate of 
under 
.
Let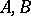 
be two subsets of a group 
, then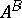 
denotes the set
 |
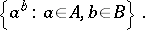For some fixed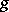 
in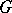 
and some subset 
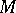of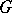 
the set 
is said to be conjugate to the set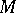 
in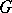 
. In particular, two subgroups 
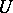and 
are called conjugate subgroups if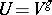 
for some 
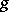in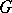 
. If a subgroup 
coincides with 
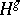for every 
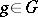(that is, 
consists of all conjugates of all its elements), then 
is called a normal subgroup of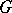 
(or an invariant subgroup, or, rarely, a self-conjugate subgroup).
Comments
Conjugacy of elements is an equivalence relation on $G$, and the equivalence classes are the conjugacy classes of $G$.
The map $x \mapsto g^{-1} x g$ for given $g$ is conjugation by $g$: it is an inner automorphism of $G$.
References
| [a1] | B. Huppert, "Endliche Gruppen" , 1 , Springer (1967) |
| [a2] | D. Gorenstein, "Finite groups" , Chelsea, reprint (1980) |
Conjugate elements. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjugate_elements&oldid=35117