Interpretation (Formalized Language)

2020 Mathematics Subject Classification: Primary: 68P05 [MSN][ZBL]

Interpretations establish a relationship between syntax and semantics. The syntax is represented by the terms $T(\Sigma,X)$ constructable by the symbols given by the signature $\Sigma=(S,F)$ and a set $X$ of variables, whereas the semantics is defined by a $\Sigma$-algebra $A$. An interpretation $v^\ast \colon T(\Sigma,X) \longrightarrow A$ always relies on an assignement $B(A,X)\ni v\colon X\longrightarrow A$, which is extended from variables $X$ to terms $T(\Sigma,X)$.

Definition of Interpretations

Let a signature $\Sigma=(S,F)$, a set $X$ of variables, and a $\Sigma$-algebra $A$ be given. For an assignement $v\in B(A,X)$ written as $v\colon X \rightarrow \bigcup_{s\in S} s^A$ it exists a unique $\Sigma$-algebra-morphism $v^\ast\colon T(\Sigma,X) \longrightarrow \bigcup_{s\in S} s^A$, which extends $v$, i.e. which fulfills $v^\ast_s (x) = v_s(x)$ for all $s \in S$, $x \in X$ [ST99] [W90]. This extension is called an interpretation with respect to the assignement $v$ and written as $t[v]$ for a term $t\in T(\Sigma,X)$. Sometimes it is also called extended assignement. Ground terms $t\in T(\Sigma)$, i.e. terms which do not contain any variable $x\in X$, have an interpretation independent from $v$.

Whereas an assignement makes only a concretion of the variables in the set $X$, an interpretations concretizes a whole term $t\in T(\Sigma,X)$ containing variables. It relates terms --- having a syntactical origin --- and $\Sigma$-algebras, which provides a semantics in the final.

An inductive definition of an interpretation $t[v]$ is given in [EM85]:

• For $x\in X_s$, it holds $x[v] := v(x)$
• For $f\in F$ with ar$(f)=0$, it holds $f[v]:= f^A$
• For $f\in F$ with type$(f)= s_1\times\cdots\times s_n \longrightarrow s$ and for $t_i\in T_{s_i}(\Sigma,X)$, it holds $f(t_1,\ldots,t_n)[v]:= f^A(t_1[v],\ldots,t_n[v])$

Interpretations and Morphisms

The special properties of interpretations enable the statement of some compatibility theorems. These theorems describe the relationship between several interpretation mappings as well as between interpretaions and $\Sigma$-algebra-morphisms. Here, at first two theorems concerning general $\Sigma$-algebras are given. Afterwards, the special situation for term-generated $\Sigma$-algebras is discussed.

Let $Y$ be another set of variables with $X\cap Y=\emptyset$. Furthermore, let

• $B(A,X)\ni v_x\colon X\longrightarrow A$
• $B(A,Y)\ni v_y\colon Y\longrightarrow A$
• $B(T(\Sigma,Y),X)\ni v\colon X\longrightarrow T(\Sigma,Y)$

be assignements. Then $v_x=v_y^\ast\circ v$ implies $v_x^\ast= v_y^\ast\circ v^\ast$ [EM85]. Now, let $B$ be another $\Sigma$-algebra. Furthermore, let the following mappings be given:

• A $\Sigma$-algebra-morphism $f\colon A\longrightarrow B$
• An assignement $B(A,X)\ni v_A\colon X\longrightarrow A$
• An assignement $B(B,X)\ni v_B\colon X\longrightarrow B$

Then $v_B= f\circ v_A$ implies $v_B^\ast= f\circ v_A^\ast$ [EM85].

In the special case of term-generated $\Sigma$-algebras $A,B\in \mathrm{Gen}(\Sigma)$, some stronger statements can be made [W90]. First of all, a morphisms between $A$ and $B$ is uniquely determined by the corresponding assignements of variables. As an immediate consequence, it exists at most one $\Sigma$-algebra-morphism $f$ between two $\Sigma$-algebras $A$ and $B$. If it exists a $\Sigma$-algebra-morphism $f'\colon A\longrightarrow B$ and a $\Sigma$-algebra-morphism $f''\colon B\longrightarrow A$, then it holds $A\cong B$.

Special Topics

Substitution Theorem

For terms $t,w\in T(\Sigma,X)$, variables $x\in X$, and assignements $v\in B(A,X)$ it holds $t[x\leftarrow w][v] = t[v[x\leftarrow w[v]]]$ [M89].

Coincidence Theorem

Let $t\in T(\Sigma,X)$ be a term. If for assignement $v_1,v_2\in B(A,X)$ it holds $\forall x\in V(t) \colon v_1(x)=v_2(x)$, then it also holds $t[v_1]=t[v_2]$.

Interpretations and Reduct

Let a signature morphism $\sigma\colon \Sigma \longrightarrow \Sigma'$ be given. Let $X$ be an $S$-sorted set of variables such that $X_s$ and $X_{s'}$ are disjoint for $s \neq s'$, $s,s' \in S$, and $X' = (\bigcup\limits_{\sigma(s)=s'} X_s)_{s'\in S'}$. Let $A'$ be a $\Sigma'$-algebra and $v' \colon X' \longrightarrow A'$ be an assignement. Define $v \colon X \longrightarrow A' |_\sigma$ by $v_s(x) = (v')_{\sigma(s)}(x)$ for $s\in S$ and $x \in X$. Then for any $\Sigma$-term $t \in T(\Sigma,X)$, $v^\ast(t) = (v')^\ast(\sigma(t))$. In particular, if $t$ is a ground term, then $t^{A' |_\sigma} = \sigma(t)^{A'}$ [ST99].

Relationship between Evaluations, Assignements and Interpretations

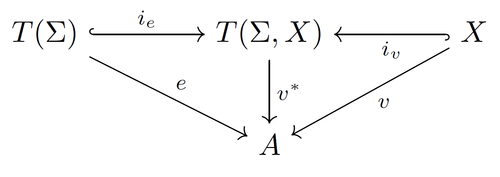
Let $v\in B(A,X)$ be an interpretation $v\colon T(\Sigma,X) \longrightarrow A$. Then the diagram

commutes, if $\bar a \circ i_a = e$ and $\bar a \circ i_v = a$ [EM85].

References

[EM85]	H. Ehrig, B. Mahr: "Fundamentals of Algebraic Specifications", Volume 1, Springer 1985
[EM90]	H. Ehrig, B. Mahr: "Fundamentals of Algebraic Specifications", Volume 2, Springer 1990
[M89]	B. Möller: "Algorithmische Sprachen und Methodik des Programmierens I", lecture notes, Technical University Munich 1989
[ST99]	D. Sannella, A. Tarlecki, "Algebraic Preliminaries", in Egidio Astesiano, Hans-Joerg Kreowski, Bernd Krieg-Brueckner, "Algebraic Foundations of System Specification", Springer 1999
[W90]	M. Wirsing: "Algebraic Specification", in J. van Leeuwen: "Handbook of Theoretical Computer Science", Elsevier 1990