Calderón-Zygmund operator

An operator $ K $ defined on a space of sufficiently smooth functions $ \phi $ with compact support in $ \mathbf R ^ {n} $ by the formula

$$ K \phi (x) = \ \lim\limits _ {\epsilon \rightarrow 0 } \ \int\limits _ {| x - y | > \epsilon } k (x - y) \phi (y) dy, $$

where the kernel $ k $ is a homogeneous function of degree $ -n $ with zero mean value over the unit sphere $ S ^ {n - 1 } = \{ {x } : {x \in \mathbf R ^ {n} , | x | = 1 } \} $. The kernel $ k $ has the form

$$ k (x) = \ \frac{\Omega (x) }{| x | ^ {n} } , $$

where $ \Omega $, the characteristic function of $ k $, satisfies the conditions

$$ \tag{* } \Omega (tx) = \ \Omega (x) \ \ \textrm{ for } \ t > 0,\ \Omega \in L _ {1} (S), $$

$$ \int\limits _ { S } \Omega (x) dS = 0. $$

The Calderón–Zygmund operator is usually written in the form

$$ K \phi (x) = \ \textrm{ p.v. } \int\limits _ {\mathbf R ^ {n} } \phi (y) \frac{\Omega (x - y) }{| x - y | ^ {n} } \ dy; $$

here $ \textrm{ p }.v. $ denotes the principal value of the integral. In the one-dimensional case the Calderón–Zygmund operator becomes the Hilbert operator $ H $:

$$ H \phi (x) = \ \textrm{ p.v. } \int\limits _ {- \infty } ^ \infty \frac{\phi (t) }{x - t } dt. $$

The Calderón–Zygmund operator can be extended by continuity to the space $ L _ {p} ( \mathbf R ^ {n} ) $ of functions $ f $ in $ \mathbf R ^ {n} $ that are summable of degree $ p $ $ (1 < p < \infty ) $. This extension maps $ L _ {p} ( \mathbf R ^ {n} ) $ continuously into itself. If $ \Omega $ satisfies the condition (*) and also Dini's condition:

$$ \int\limits _ { 0 } ^ { 1 } { \frac{\omega (t) dt }{t} } < \infty ,\ \ \omega (t) = \ \sup _ {\begin{array}{c} | x - x ^ \prime | \leq t \\ | x | = | x ^ \prime | = 1 \end{array} } \ | \Omega (x) - \Omega (x ^ \prime ) | ; $$

and if

$$ K _ \epsilon f (x) = \ \int\limits _ {| y | > \epsilon } \frac{\Omega (y) }{| y | ^ {n} } f (x - y) dy $$

for $ 1 < p < \infty $ and $ f \in L _ {p} ( \mathbf R ^ {n} ) $, then

a) there exists a constant $ A _ {p} $( independent of $ f $ or $ \epsilon $) such that

$$ \| K _ \epsilon f \| _ {L _ {p} } \leq \ A _ {p} \| f \| _ {L _ {p} } ; $$

b) the limit $ \lim\limits _ {\epsilon \rightarrow 0 } K _ \epsilon f = Kf $ exists in the sense of convergence in $ L _ {p} $ and

$$ \| Kf \| _ {L _ {p} } \leq \ A _ {p} \| f \| _ {L _ {p} } . $$

The Calderón–Zygmund operator was analyzed by A.P. Calderón and A. Zygmund [1].

References

[1]	A.P. Calderón, A. Zygmund, "On the existence of certain singular integrals" Acta Math. , 88 (1952) pp. 85–139
[2]	S.G. Mikhlin, "Multidimensional singular integrals and integral equations" , Pergamon (1965) (Translated from Russian)
[3]	E.M. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970)

Comments

Proofs of the estimates a) and b) above can be found in [3], Chapt. II, Section 4.

In the 1960's the operators described above were often called Mikhlin–Calderón–Zygmund operators, since the main boundedness theorem for them on $ L _ {p} ( \mathbf R ^ {n} ) $( estimate a)) was proved by S.G. Mikhlin in 1938 (published in [a1]).

Nowadays the term Calderón–Zygmund operator is often used for general operators in the class defined by G. David and J.L. Journé in [a2].

Assertion b) has been generalized to singular integrals with odd kernels, and to singular integrals with even kernels $ \Omega \in L _ {2} (S ^ {n - 1 } ) $, [a3], Chapt. VI, Sections 2, 3.

See also Singular integral; Hilbert singular integral; Hilbert transform.

References

[a1]	S.G. Mikhlin, "On a boundedness theorem for a singular integral operator" Uspekhi Mat. Nauk , 8 (1953) pp. 213–217 (In Russian)
[a2]	G. David, J.L. Journé, "Une characterization des opérateurs intégraux singuliers bornés sur 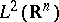" C.R. Acad. Sci. Paris , 296 (1983) pp. 761–764
[a3]	E.M. Stein, G. Weiss, "Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1975)