Positive-definite function

A complex-valued function $ \phi $ on a group $ G $ satisfying

$$ \sum _ {i,j= 1 } ^ { m } \alpha _ {i} \overline \alpha \; _ {j} \phi ( x _ {j} ^ {-} 1 x _ {i} ) \geq 0 $$

for all choices $ x _ {1} \dots x _ {m} \in G $, $ \alpha _ {1} \dots \alpha _ {m} \in \mathbf C $. The set of positive-definite functions on $ G $ forms a cone in the space $ M( G) $ of all bounded functions on $ G $ which is closed with respect to the operations of multiplication and complex conjugation.

The reason for distinguishing this class of functions is that positive-definite functions define positive functionals (cf. Positive functional) on the group algebra $ \mathbf C G $ and unitary representations of the group $ G $( cf. Unitary representation). More precisely, let $ \phi : G \rightarrow \mathbf C $ be any function and let $ l _ \phi : \mathbf C G\rightarrow \mathbf C $ be the functional given by

$$ l _ \phi \left ( \sum _ {g \in G } \alpha _ {g} g \right ) = \ \sum _ {g \in G } \phi ( g) \alpha _ {g} ; $$

then for $ l _ \phi $ to be positive it is necessary and sufficient that $ \phi $ be a positive-definite function. Further, $ l _ \phi $ defines a $ * $- representation of the algebra $ \mathbf C G $ on a Hilbert space $ H _ \phi $, and therefore a unitary representation $ \pi _ \phi $ of the group $ G $, where $ \phi ( g) = ( \pi _ \phi ( g) \xi , \xi ) $ for some $ \xi \in H _ \phi $. Conversely, for any representation $ \pi $ and any vector $ \xi \in H _ \phi $, the function $ g \rightarrow ( \pi ( g) \xi , \xi ) $ is a positive-definite function.

If $ G $ is a topological group, the representation $ \pi _ \phi $ is weakly continuous if and only if the positive-definite function is continuous. If $ G $ is locally compact, continuous positive-definite functions are in one-to-one correspondence with the positive functionals on $ L _ {1} ( G) $.

For commutative locally compact groups, the class of continuous positive-definite functions coincides with the class of Fourier transforms of finite positive regular Borel measures on the dual group. There is an analogue of this assertion for compact groups: A continuous function $ \phi $ on a compact group $ G $ is a positive-definite function if and only if its Fourier transform $ \widehat \phi ( b) $ takes positive (operator) values on each element of the dual object, i.e.

$$ \int\limits _ { G } \phi ( g) ( \sigma ( g) \xi , \xi ) dg \geq 0 $$

for any representation $ \sigma $ and any vector $ \xi \in H _ \sigma $, where $ H _ \sigma $ is the space of $ \sigma $.

References

[1]	E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 2 , Springer (1979)
[2]	M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)

Comments

The representations of $ \mathbf C G $ associated to positive functionals $ l $ mentioned above are cyclic representations. A cyclic representation of a $ C ^ {*} $- algebra $ {\mathcal A} $ is a representation $ \rho : {\mathcal A} \rightarrow B( H) $, the $ C ^ {*} $- algebra of bounded operators on the Hilbert space $ H $, such that there is a vector $ \xi \in H $ such that the closure of $ \{ {A \xi } : {A \in {\mathcal A} } \} $ is all of $ H $. These are the basic components of any representation. Indeed, if $ \rho $ is non-degenerate, i.e. $ \{ {\xi \in H } : {\rho ( A) ( \xi ) = 0 \textrm{ for all } A \in {\mathcal A} } \} = 0 $, then $ \rho $ is a direct sum of cyclic representations. Cf. also Cyclic module for an analogous concept in ring and module theory.

The cyclic representation associated to a positive functional $ l $ on $ {\mathcal A} $ is a suitably completed quotient of the regular representation. More precisely, the construction is as follows. Define an inner product on $ {\mathcal A} $ by

$$ \langle A, B \rangle = l ( A ^ {*} B ) , $$

and define a left ideal of $ {\mathcal A} $ by

$$ {\mathcal I} = \{ {A \in {\mathcal A} } : {l( A ^ {*} A ) = 0 } \} . $$

The inner product just defined descends to define an inner product on the quotient space $ {\mathcal A} / {\mathcal I} $. Now complete this space to obtain a Hilbert space $ H _ {l} $, and define the representation $ \pi _ {l} $ by:

$$ \pi _ {l} ( A) ([ B ]) \simeq [ AB], $$

where $ [ B] $ denotes the class of $ B \in {\mathcal A} $ in $ {\mathcal A} / {\mathcal I} \subset H _ {l} $. The operator $ \pi _ {l} ( A) $ extends to a bounded operator on $ H _ {l} $.

If $ {\mathcal A} $ contains an identity, then the class of that identity is a cyclic vector for $ \pi _ {l} $. If $ {\mathcal A} $ does not contain an identity, such is first adjoined to obtain a $ C ^ {*} $- algebra $ {\mathcal A} tilde $ and the construction is repeated for $ {\mathcal A} tilde $. To prove that then the class of 1 is cyclic for $ {\mathcal A} $( not just $ {\mathcal A} tilde $) one uses an approximate identity for $ {\mathcal I} $, i.e. a net (directed set) $ \{ E _ \alpha \} $ of positive elements $ E _ \alpha \in {\mathcal I} $ such that $ \| E _ \alpha \| \leq 1 $, $ \alpha \leq \beta $ implies $ E _ \alpha \leq E _ \beta $ and $ \lim\limits _ \alpha \| AE _ \alpha - A \| = 0 $ for all $ A \in {\mathcal I} $. Such approximate identities always exist. See e.g. [1], vol. 1, p. 321 and [a5], Sects. 2.2.3, 2.3.1 and 2.3.3 for more details on all this.

A positive functional on a $ C ^ {*} $- algebra of norm 1 is often called a state, especially in the theoretical physics literature.

References

[a1]	S. Bochner, "Lectures on Fourier integrals" , Princeton Univ. Press (1959) (Translated from German)
[a2]	W. Rudin, "Fourier analysis on groups" , Wiley (1962)
[a3]	H. Reiter, "Classical harmonic analysis and locally compact groups" , Clarendon Press (1968)
[a4]	J. Dixmier, "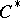 algebras" , North-Holland (1977) (Translated from French)
[a5]	O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , 1 , Springer (1979)