Convergence in distribution
2020 Mathematics Subject Classification: Primary: 60B10 [MSN][ZBL]
Convergence of a sequence of random variables  defined on a certain probability space
defined on a certain probability space  , to a random variable
, to a random variable  , defined in the following way:
, defined in the following way:  if
if
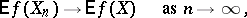 | (*) |
for any bounded continuous function  . This form of convergence is so called because condition (*) is equivalent to the convergence of the distribution functions
. This form of convergence is so called because condition (*) is equivalent to the convergence of the distribution functions  to the distribution function
to the distribution function  at every point
at every point  at which
at which 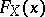 is continuous.
is continuous.
Comments
See also Convergence, types of; Distributions, convergence of.
This is special terminology for real-valued random variables for what is generally known as weak convergence of probability measures (same definition as in (*), but with 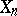 ,
, 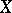 taking values in possibly more general spaces).
taking values in possibly more general spaces).
Convergence in distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convergence_in_distribution&oldid=19094