Polynomial of best approximation

A polynomial furnishing the best approximation of a function $x ( t)$ in some metric, relative to all polynomials constructed from a given (finite) system of functions. If $X$ is a normed linear function space (such as $C [ a, b]$ or $L _ {p} ( a, b)$, $p \geq 1$), and if

$$U _ {n} = \{ u _ {1} ( t) \dots u _ {n} ( t) \}$$

is a system of linearly independent functions in $X$, then for any $x \in X$ the (generalized) polynomial of best approximation

$$\tag{* } \widetilde{u} ( t) = \widetilde{u} ( x, t) = \ \sum _ {k = 1 } ^ { n } \widetilde{c} _ {k} u _ {k} ( t),$$

defined by the relation

$$\| x - \widetilde{u} \| = \ \min _ {\{ c _ {k} \} } \left \| x - \sum _ {k = 1 } ^ { n } c _ {k} u _ {k} \right \| ,$$

exists. The polynomial of best approximation is unique for all $x \in X$ if $X$ is a space with a strictly convex norm (i.e. if $\| x \| = \| y \|$ and $x \neq y$, then $\| x + y \| < \| x \| + \| y \|$). This is the case for $L _ {p} ( a, b)$, $1 < p < \infty$. In $C [ a, b]$, which has a norm that is not strictly convex, the polynomial of best approximation for any $x \in C [ a, b]$ is unique if $U _ {n}$ is a Chebyshev system on $[ a, b]$, i.e. if each polynomial

$$u ( t) = \sum _ {k = 1 } ^ { n } c _ {k} u _ {k} ( t) \neq 0$$

has at most $n - 1$ zeros on $[ a, b]$. In particular, one has uniqueness in the case of the (usual) algebraic polynomials in $C [ a, b]$, and also for the trigonometric polynomials in the space $C _ {2 \pi }$ of continuous $2 \pi$- periodic functions on the real line, with the uniform metric. If the polynomial of best approximation exists and is unique for any $x \in X$, it is a continuous function of $x$.

Necessary and sufficient conditions for a polynomial to be a best approximation in the spaces $C[ a, b]$ and $L _ {p} [ a, b]$ are known. For example, one has Chebyshev's theorem: If $U _ {n}$ is a Chebyshev system, then the polynomial (*) is a polynomial of best approximation for a function $x \in C [ a, b]$ in the metric of $C [ a, b]$ if and only if there exists a system of $n + 1$ points $t _ {i}$, $a \leq t _ {1} < {} \dots < t _ {n + 1 } \leq b$, at which the difference

$$\Delta ( t) = x ( t) - \widetilde{u} ( t)$$

assumes values

$$\pm \max _ {a \leq t \leq b } | \Delta ( t) |$$

and, moreover,

$$\Delta ( t _ {i + 1 } ) = - \Delta ( t _ {i} ),\ \ i = 1 \dots n.$$

The polynomial (*) is a polynomial of best approximation for a function $x ( t) \in L _ {p} [ a, b]$, $p > 1$, in the metric of that space, if and only if for $k = 1 \dots n$,

$$\int\limits _ { a } ^ { b } u _ {k} ( t) | x ( t) - \widetilde{u} ( t) | ^ {p - 1 } \ \mathop{\rm sign} [ x ( t) - \widetilde{u} ( t)] dt = 0.$$

In $L _ {1} [ a, b]$, the conditions

$$\int\limits _ { a } ^ { b } u _ {k} ( t) \mathop{\rm sign} [ x ( t) - \widetilde{u} ( t)] dt = 0,\ \ k = 1 \dots n,$$

are sufficient for $\widetilde{u} ( t)$ to be a polynomial of best approximation for $x \in L _ {1} [ a, b]$, and if the measure of the set of all points $t \in ( a, b)$ at which $x ( t) = \widetilde{u} ( t)$ is zero, they are also necessary; see also Markov criterion.

There exist algorithms for the approximate construction of polynomials of best uniform approximation (see e.g. [3], [5]).

References

[1]	N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian)
[2]	N.P. Korneichuk, "Extremal problems in approximation theory" , Moscow (1976) (In Russian)
[3]	V.K. Dzyadyk, "Introduction to the theory of uniform approximation of functions by polynomials" , Moscow (1977) (In Russian)
[4]	V.M. Tikhomirov, "Some problems in approximation theory" , Moscow (1976) (In Russian)
[5]	P.J. Laurent, "Approximation et optimisation" , Hermann (1972)
[6]	E.Ya. Remez, "Foundations of numerical methods of Chebyshev approximation" , Kiev (1969) (In Russian)

References

[a1]	A.M. Pinkus, "On 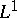-approximation" , Cambridge Univ. Press (1989)
[a2]	A. Schönhage, "Approximationstheorie" , de Gruyter (1971)
[a3]	G.A. Watson, "Approximation theory and numerical methods" , Wiley (1980)
[a4]	E.W. Cheney, "Introduction to approximation theory" , McGraw-Hill (1966) pp. Chapts. 4&6
[a5]	M.J.D. Powell, "Approximation theory and methods" , Cambridge Univ. Press (1981)
[a6]	J.R. Rice, "The approximation of functions" , 1. Linear theory , Addison-Wesley (1964)
[a7]	T.J. Rivlin, "An introduction to the approximation of functions" , Blaisdell (1969)