Positive element

of an algebra $A$ with an involution ${} ^ {*}$

An element $x$ of $A$ of the form $x = y ^ {*} y$, where $y \in A$. The set $P( A)$ of positive elements in a Banach $*$- algebra $A$ contains the set $Q( A)$ of squares of the Hermitian elements, which in turn contains the set $P _ {0} ( A) ^ {+}$ of all Hermitian elements with positive spectrum (cf. Spectrum of an element), but in general it does not contain the set $A ^ {+}$ of all Hermitian elements with non-negative spectrum. The condition $P( A) \subset A ^ {+}$ defines the class of completely-symmetric (or Hermitian) Banach $*$- algebras. For a $*$- algebra to be completely symmetric it is necessary and sufficient that all Hermitian elements in it have real spectrum. The equality $P( A) = A ^ {+}$ holds if and only if $A$ is a $C ^ {*}$- algebra. In that case $P( A)$ is a reproducing cone (cf. Semi-ordered space) in the space of all Hermitian elements of the algebra $A$.

References

[1]	M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)
[2]	J. Dixmier, "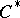 algebras" , North-Holland (1977) (Translated from French)
[3]	D.N. Raikov, Dokl. Akad. Nauk. SSSR , 54 : 5 (1946) pp. 391–394
[4]	V. Pták, "On the spectral radius in Banach algebras with involution" Bull. London Math. Soc. , 2 (1970) pp. 327–334
[5]	T.W. Palmer, "Hermitian Banach -algebras" Bull. Amer. Math. Soc. , 78 (1972) pp. 522–524