Sobolev space

A space $W^l_p(\Omega)$ of functions $f=f(x)=f(x_1,\ldots,x_n)$ on a set $\Omega\subset\RR^n$ (usually open) such that the $p$-th power of the absolute value of $f$ and of its generalized derivatives (cf. Generalized derivative) up to and including order $l$ are integrable ($1\leq p\leq \infty$).

The norm of a function $f\in W^l_p(\Omega)$ is given by \begin{equation*} \lVert f\rVert_{W^l_p(\Omega)}=\sum_{\lvert k\rvert\leq l} \lVert f^{(k)}\rVert_{L_p(\Omega)}. \end{equation*} Here \begin{equation*} f^{(k)}=\frac{\partial^{\lvert k\rvert}f}{\partial x_1^{k_1}\cdots \partial x_n^{k_n}},\qquad f^{(0)}=f, \end{equation*} is the generalized partial derivative of $f$ of order $\lvert k\rvert=\sum_{j=1}^n k_j$, and \begin{equation*} \lVert \psi\rVert_{L_p(\Omega)} =\left( \int_\Omega \lvert\psi(x)\rvert^p\,dx \right)^{1/p} \qquad (1\leq p\leq \infty). \end{equation*}

When 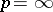, this norm is equal to the essential supremum:

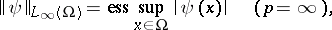that is, to the greatest lower bound of the set of all 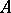for which 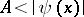on a set of measure zero.

The space 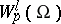was defined and first applied in the theory of boundary value problems of mathematical physics by S.L. Sobolev (see [1], [2]).

Since its definition involves generalized derivatives rather than ordinary ones, it is complete, that is, it is a Banach space.

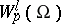is considered in conjunction with the linear subspace 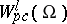consisting of functions having partial derivatives of order 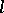that are uniformly continuous on . 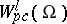has advantages over 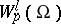, although it is not closed in the metric of 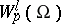and is not a complete space. However, for a wide class of domains (those with a Lipschitz boundary, see below) the space 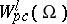is dense in 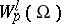for all 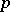, , 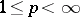that is, for such domains the space 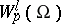acquires a new property in addition to completeness, in that every function belonging to it can be arbitrarily well approximated in the metric of by functions from .

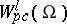It is sometimes convenient to replace the expression (1) for the norm of 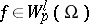by the following:

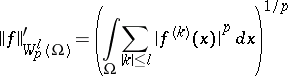(1prm)

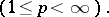The norm (1prm) is equivalent to the norm (1) i.e. 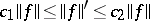, where 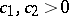do not depend on 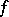. When 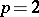, (1prm) is a Hilbert norm, and this fact is widely used in applications.

The boundary 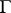of a bounded domain is said to be Lipschitz if for any 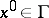there is a rectangular coordinate system 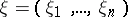with origin 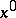so that the box

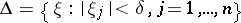is such that the intersection 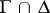is described by a function 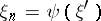, with

which satisfies on 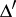(the projection of 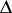onto the plane 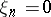) the Lipschitz condition

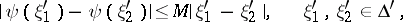where the constant 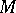does not depend on the points 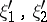, and . All smooth and many piecewise-smooth boundaries are Lipschitz boundaries.

For a domain with a Lipschitz boundary, (1) is equivalent to the following:

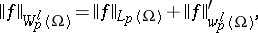where

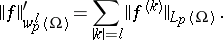One can consider more general anisotropic spaces (classes) 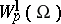, where 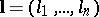is a positive vector (see Imbedding theorems). For every such vector one can define, effectively and to a known extent exhaustively, a class of domains 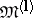with the property that if 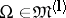, then any function 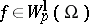can be extended to 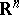within the same class. More precisely, it is possible to define a functi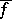on on 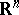with the properties

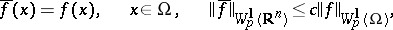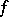where does not depend on (see [3]).

In virtue of this property, inequalities of the type found in imbedding theorems for functions 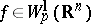automatically carry over to functions , .

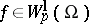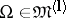For vectors 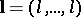, the domains 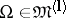have Lipschitz boundaries, and .

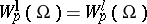The investigation of the spaces (classes) 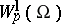(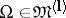) is based on special integral representations for functions belonging to these classes. The first such representation was obtained (see [1], [2]) for an isotropic space 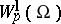of a domain , star-shaped with respect to some sphere. For the further development of this method see, for example, [3].

The classes 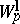and 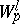can be generalized to the case of fractional 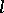, or vectors 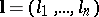with fractional components .

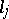The space 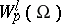can also be defined for negative integers 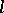. Its elements are usually generalized functions, that is, linear functionals 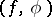on infinitely-differentiable functions 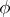with compact support in .

By definition, a generalized function 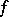belongs to the class 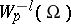(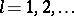) if

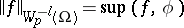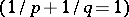is finite, where the supremum is taken over all functions with norm at most one . The functions 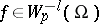form the space adjoint to the Banach space .

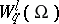References

[1]	S.L. Sobolev, "On a theorem of functional analysis" Transl. Amer. Math. Soc. (2) , 34 (1963) pp. 39–68 Mat. Sb. , 4 (1938) pp. 471–497
[2]	S.L. Sobolev, "Some applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian)
[3]	O.V. Besov, V.P. Il'in, S.M. Nikol'skii, "Integral representations of functions and imbedding theorems" , 1–2 , Wiley (1978) (Translated from Russian)
[4]	S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian)

References

[a1]	V.G. Maz'ja, "Sobolev spaces" , Springer (1985)
[a2]	F. Trèves, "Basic linear partial differential equations" , Acad. Press (1975) pp. Sects. 24–26
[a3]	R.A. Adams, "Sobolev spaces" , Acad. Press (1975)