Genus of a surface

A numerical birational invariant of a two-dimensional algebraic variety defined over an algebraically closed field 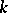. There are two different genera — the arithmetic genus and the geometric genus. The geometric genus 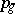of a complete smooth algebraic surface 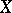is equal to

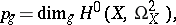i.e. to the dimension of the space of regular differential -forms (cf. Differential form) on 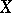. The arithmetic genus 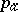of a complete smooth algebraic surface is equal to

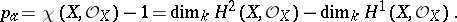The geometric and arithmetic genera of a complete smooth algebraic surface 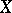are related by the formula 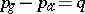, where 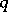is the irregularity of 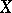, which is equal to the dimension of the space of regular differential 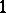-forms on .

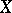References

[1]	I.R., et al. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) MR1392959 MR1060325 Zbl 0830.00008 Zbl 0733.14015 Zbl 0832.14026 Zbl 0509.14036 Zbl 0492.14024 Zbl 0379.14006 Zbl 0253.14006 Zbl 0154.21001

References

[a1]	R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001
[a2]	A. van de Ven, "Compact complex surfaces" , Springer (1984) Zbl 0718.14023
[a3]	P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001