Dickman-function(2)

The unique continuous solution of the system

$$ \rho ( u ) = 1 ( 0 \leq u \leq 1 ) , $$

$$ u \rho ^ \prime ( u ) = - \rho ( u - 1 ) ( u > 1 ) . $$

The Dickman function $ \rho ( u ) $ occurs in the problem of estimating the number $ \Psi ( x,y ) $ of positive integers not exceeding $ x $ that are free of prime factors greater than $ y $: for any fixed $ u > 0 $, one has $ \Psi ( x,x ^ { {1 / u } } ) \sim \rho ( u ) x $ as $ u \rightarrow \infty $[a2], [a4].

The function $ \rho ( u ) $ is positive, non-increasing and tends to zero at a rate faster than exponential as $ u \rightarrow \infty $. A precise asymptotic estimate is given by the de Bruijn–Alladi formula [a1], [a3]:

$$ \rho ( u ) = ( 1 + O ( { \frac{1}{u} } ) ) \sqrt { { \frac{\xi ^ \prime ( u ) }{2 \pi } } } \times $$

$$ \times { \mathop{\rm exp} } \left \{ \gamma - u \xi ( u ) + \int\limits _ { 0 } ^ { \xi ( u ) } { { \frac{e ^ {s} - 1 }{s} } } {ds } \right \} ( u > 1 ) , $$

where $ \gamma $ is the Euler constant and $ \xi ( u ) $ is the unique positive solution of the equation $ e ^ {\xi ( u ) } = 1 + u \xi ( u ) $.

References

[a1]	K. Alladi, "The Turán–Kubilius inequality for integers without large prime factors" J. Reine Angew. Math. , 335 (1982) pp. 180–196
[a2]	N.G. de Bruijn, "On the number of positive integers and free of prime factors 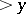" Nederl. Akad. Wetensch. Proc. Ser. A , 54 (1951) pp. 50–60
[a3]	N.G. de Bruijn, "The asymptotic behaviour of a function occurring in the theory of primes" J. Indian Math. Soc. (N.S.) , 15 (1951) pp. 25–32
[a4]	A. Hildebrand, G. Tenenbaum, "Integers without large prime factors" J. de Théorie des Nombres de Bordeaux , 5 (1993) pp. 411–484