Power residue
modulo $m$
An integer $a$ for which the congruence $$ x^n \equiv a \pmod m $$ is solvable for a given integer $n > 1$. The number $a$ is called a residue of degree $n$ modulo $m$. If this congruence is not solvable, then $a$ is called a non-residue of degree $n$ modulo $m$. When $n=2$, the power residues and non-residues are said to be quadratic, when $n=3$, cubic, and when $n=4$, biquadratic or quartic.
In the case of a prime modulus $p$, the question of the solvability of the congruence $x^n \equiv a \pmod p$ can be answered by using the Euler criterion: If $q = \mathrm{hcf}(n,p-1)$, then for the congruence $x^n \equiv a \pmod p$ to be solvable it is necessary and sufficient that $$ a^q \equiv 1 \pmod p\ . $$
When this condition is fulfilled, the original congruence has $q$ different solutions modulo $p$. It follows from this test that among the numbers $1,\ldots,p-1$ there are exactly $(p-1)/q$ residues and $(q-1)(p-1)/q$ non-residues of degree $n$ modulo $p$. See Distribution of power residues and non-residues.
Comments
As in the case of quadratic residues one defines a power-residue symbol. Let 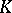 be a number field containing the
be a number field containing the  -th roots of unity. Let
-th roots of unity. Let 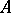 be the ring of integers of
be the ring of integers of 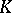 and let
and let 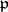 be a prime ideal of
be a prime ideal of 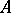 . Let
. Let 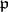 be relatively prime to
be relatively prime to  and
and 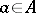 . If
. If 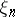 is a primitive
is a primitive  -th root of unity, one has
-th root of unity, one has
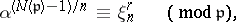 |
where 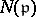 is the norm of
is the norm of 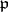 , i.e. the number of elements of
, i.e. the number of elements of 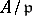 . One now defines the power-residue symbol
. One now defines the power-residue symbol
 |
If 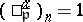 , then
, then  is an
is an  -th power residue modulo
-th power residue modulo 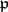 , i.e.
, i.e. 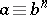 (
(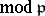 ) is solvable for
) is solvable for 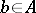 . If
. If  ,
, 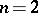 and
and 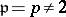 , one finds back the quadratic-residue symbol, cf. Legendre symbol.
, one finds back the quadratic-residue symbol, cf. Legendre symbol.
There also exist power-residue reciprocity laws, cf. e.g. [a2], which specialize to the quadratic reciprocity law if 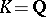 ,
, 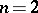 .
.
References
| [a1] | W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , Springer & PWN (1990) pp. 394ff |
| [a2] | J. Neukirch, "Class field theory" , Springer (1986) pp. Chapt. IV, §9 |
Power residue. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Power_residue&oldid=15394