Pisot number
Pisot–Vijayaraghavan number
A real algebraic integer  , all of whose other Galois conjugates have absolute value strictly less than
, all of whose other Galois conjugates have absolute value strictly less than  (cf. also Galois theory). That is,
(cf. also Galois theory). That is,  satisfies a polynomial equation of the form
satisfies a polynomial equation of the form  , where the
, where the  are integers,
are integers,  and the roots of
and the roots of  other than
other than  all lie in the open unit circle
all lie in the open unit circle  . The set of these numbers is traditionally denoted by
. The set of these numbers is traditionally denoted by  . Every positive integer
. Every positive integer  is a Pisot number, but a more interesting example is the golden ratio
is a Pisot number, but a more interesting example is the golden ratio 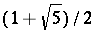 . Every real number field
. Every real number field 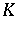 contains infinitely many Pisot numbers of degree equal to
contains infinitely many Pisot numbers of degree equal to  , and, in fact, every real number field
, and, in fact, every real number field 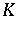 can be generated by Pisot numbers, even by Pisot units (
can be generated by Pisot numbers, even by Pisot units ( ).
).
The Pisot numbers have the interesting property that if 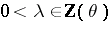 , then
, then 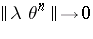 as
as 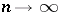 , where here
, where here 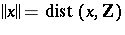 denotes the distance from
denotes the distance from  to the nearest integer. It is an open question whether this property characterizes
to the nearest integer. It is an open question whether this property characterizes  among the real numbers
among the real numbers 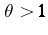 (Pisot's conjecture). An important result of Ch. Pisot in this direction is that if
(Pisot's conjecture). An important result of Ch. Pisot in this direction is that if 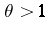 and
and 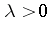 are real numbers for which
are real numbers for which 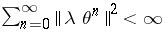 , then
, then 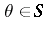 and
and 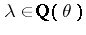 [a1].
[a1].
The unusual behaviour of the powers of Pisot numbers leads to applications in harmonic analysis, [a3], [a5], dynamical systems theory (cf. also Dynamical system) [a6] and the theory of quasi-crystals [a4]. For example, if 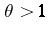 , then the set of powers
, then the set of powers 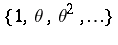 is harmonious if and only if
is harmonious if and only if 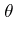 is a Pisot number or a Salem number [a3]. The Bragg spectrum of the diffraction pattern of a self-similar tiling (cf., e.g., Voronoi lattice types) is non-trivial if and only if the scaling factor of the tiling is a Pisot number [a4].
is a Pisot number or a Salem number [a3]. The Bragg spectrum of the diffraction pattern of a self-similar tiling (cf., e.g., Voronoi lattice types) is non-trivial if and only if the scaling factor of the tiling is a Pisot number [a4].
A surprising fact is that  is a closed and hence nowhere-dense subset of the real line [a5]. The derived sets
is a closed and hence nowhere-dense subset of the real line [a5]. The derived sets 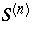 are all non-empty and
are all non-empty and 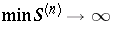 as
as 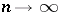 . (Here
. (Here 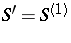 denotes the set of limit points of
denotes the set of limit points of 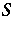 ,
,  the set of limit points of
the set of limit points of  , etc., cf. also Limit point of a set). The order type of
, etc., cf. also Limit point of a set). The order type of  is described in [a2]. The smallest elements of
is described in [a2]. The smallest elements of  ,
, 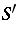 and
and 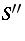 are explicitly known [a1].
are explicitly known [a1].
There is an intimate relationship between the set  of Pisot numbers and the set
of Pisot numbers and the set  of Salem numbers. It is known that
of Salem numbers. It is known that 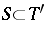 , cf. Salem number. It seems reasonable to conjecture that
, cf. Salem number. It seems reasonable to conjecture that 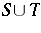 is closed and that
is closed and that  , but it is not yet known whether or not
, but it is not yet known whether or not 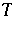 is dense in
is dense in 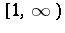 .
.
References
| [a1] | M.J. Bertin, A. Decomps-Guilloux, M. Grandet-Hugot, M. Pathiaux-Delefosse, J.P. Schreiber, "Pisot and Salem Numbers" , Birkhäuser (1992) |
| [a2] | D.W. Boyd, R.D. Mauldin, "The order type of the set of Pisot numbers" Topology Appl. , 69 (1996) pp. 115–120 |
| [a3] | Y. Meyer, "Algebraic numbers and harmonic analysis" , North-Holland (1972) |
| [a4] | "The mathematics of long-range aperiodic order" R.V. Moody (ed.) , Kluwer Acad. Publ. (1997) |
| [a5] | R. Salem, "Algebraic numbers and Fourier analysis" , Heath (1963) |
| [a6] | K. Schmidt, "On periodic expansions of Pisot numbers and Salem numbers" Bull. London Math. Soc. , 12 (1980) pp. 269–278 |
Pisot number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pisot_number&oldid=15094