M-dependent-process
A discrete-time stochastic process $ ( X _ {n} ) _ {n \in \mathbf Z } $
is $ m $-
dependent if for all $ k $
the joint stochastic variables $ ( X _ {n} ) _ {n \leq k } $
are independent of the joint stochastic variables $ ( X _ {n} ) _ {n \geq k + m + 1 } $.
Such processes arise naturally as limits of rescaling transformations (renormalizations) and (hence) as examples of processes with scaling symmetries [a1]. Examples of $ m $- dependent processes are given by $ ( m + 1 ) $- block factors. These are defined as follows. Let $ ( Z _ {n} ) _ {n \in \mathbf Z } $ be an independent process and $ \phi $ a function of $ m + 1 $ variables; let $ X _ {n} = f ( Z _ {n} \dots Z _ {n+} m ) $; then the $ ( m + 1 ) $- block factor $ X _ {n} $ is an $ m $- dependent process.
There are one-dependent processes which are not $ 2 $- block factors, [a2].
References
| [a1] | G.L. O'Brien, "Scaling transformations for 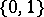 -valued sequences" Z. Wahrscheinlichkeitstheorie Verw. Gebiete , 53 (1980) pp. 35–49 -valued sequences" Z. Wahrscheinlichkeitstheorie Verw. Gebiete , 53 (1980) pp. 35–49 |
| [a2] | J. Aaronson, D. Gilat, M. Keane, V. de Valk, "An algebraic construction of a class of one-dependent processes" Ann. Probab. , 17 (1988) pp. 128–143 |
| [a3] | S. Janson, "Runs in 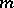 -dependent sequences" Ann. Probab. , 12 (1984) pp. 805–818 -dependent sequences" Ann. Probab. , 12 (1984) pp. 805–818 |
| [a4] | G. Haiman, "Valeurs extrémales de suites stationaires de variable aléatoires 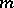 -dépendantes" Ann. Inst. H. Poincaré Sect. B (N.S.) , 17 (1981) pp. 309–330 -dépendantes" Ann. Inst. H. Poincaré Sect. B (N.S.) , 17 (1981) pp. 309–330 |
M-dependent-process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=M-dependent-process&oldid=14932