Morley rank
An important notion and tool in model theory, a branch of mathematical logic. The Morley rank is an ordinal-valued dimension associated to first-order formulas with parameters from a model $ M $
of a complete first-order theory $ T $.
It is defined inductively by: $ { \mathop{\rm Morleyrank} } \theta ( x ) \geq \alpha + 1 $
if there is an elementary extension $ N $
of $ M $
and infinitely many formulas $ \phi _ {i} ( x ) $(
$ i < \omega $)
with parameters from $ N $
such that the $ \phi _ {i} ( x ) $
are pairwise inconsistent, $ N \vDash \phi _ {i} ( x ) \rightarrow \theta ( x ) $
for all $ i $
and $ { \mathop{\rm Morleyrank} } \phi _ {i} ( x ) \geq \alpha $
for all $ i $.
For $ \delta $
a limit ordinal (cf. also Ordinal number), $ { \mathop{\rm Morleyrank} } \theta ( x ) \geq \delta $
if $ { \mathop{\rm Morleyrank} } \theta ( x ) \geq \alpha $
for all $ \alpha < \delta $.
The Morley rank of $ \theta ( x ) $
is said to be equal to $ \alpha $
if it is greater than or equal to $ \alpha $
but not greater than or equal to $ \alpha + 1 $.
The Morley rank of $ \theta ( x ) $
is said to be $ \infty $(
or undefined) if it is not equal to any ordinal.
The Morley rank was introduced by M. Morley [a2] in his study of countable theories $ T $ such that for some uncountable cardinal number $ \kappa $, $ T $ has a unique model of cardinality $ \kappa $. Morley showed that a theory $ T $ satisfying the latter condition has a unique model of cardinality $ \lambda $ for any uncountable cardinal $ \lambda $. An important part of his work was to show that every formula has ordinal-valued Morley rank. Subsequently, J.T. Baldwin [a1] showed that under Morley's hypothesis, every formula has finite Morley rank.
A classical example of Morley rank occurs in the (complete) theory $ ACF _ {0} $ of algebraically closed fields of characteristic $ 0 $. The field $ \mathbf C $ of complex numbers is a model, and for a formula $ \phi ( x _ {1} \dots x _ {n} ) $ with parameters in $ \mathbf C $ defining a non-singular algebraic variety $ V $, the Morley rank of $ \phi $ is precisely the dimension of $ V $ as a complex manifold.
Following the example of Morley rank, S. Shelah [a3] defined a host of rank-functions associated to formulas in first-order theories, which play an important role in classification theory.
See also Group of finite Morley rank.
References
| [a1] | J.T. Baldwin, "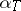 is finite for is finite for 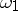 -categorical -categorical 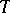 " Trans. Amer. Math. Soc. , 181 (1973) pp. 37–51 " Trans. Amer. Math. Soc. , 181 (1973) pp. 37–51 |
| [a2] | M.D. Morley, "Categoricity in power" Trans. Amer. Math. Soc. , 114 (1965) pp. 514–538 |
| [a3] | S. Shelah, "Classification theory and the number of non-isomorphic models" , North-Holland (1990) (Edition: Revised) |
Morley rank. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morley_rank&oldid=14510