Zygmund class of functions

Let $ M $ be a positive real number. The Zygmund class $ Z _ {M} $ is the class of continuous $ 2 \pi $- periodic functions $ f $ with the property that for all $ x $ and all $ h > 0 $ the inequality

$$ | f ( x + h ) - 2f ( x) + f ( x - h ) | \leq M h $$

holds. The class $ Z _ {M} $ was introduced by A. Zygmund [1]. In terms of this class one can obtain a conclusive solution to the Jackson–Bernstein problem on direct and inverse theorems in the theory of approximation of functions (cf. Bernstein theorem; Jackson theorem). For example: A continuous $ 2 \pi $- periodic function $ f $ belongs to the Zygmund class $ Z _ {M} $ for some $ M > 0 $ if and only if its best uniform approximation error $ E _ {n} ( f ) $ by trigonometric polynomials of degree $ \leq n $ satisfies the inequality

$$ E _ {n} ( f ) \leq \frac{A}{n} , $$

where $ A > 0 $ is a constant. The modulus of continuity $ \omega ( \delta , f ) $ of any function $ f \in Z _ {M} $ admits the estimate

$$ \omega ( \delta , f ) \leq \frac{M}{2 \mathop{\rm ln} \sqrt {2 } + 1 } \delta \mathop{\rm ln} \frac \pi \delta + O ( \delta ) $$

in which the constant $ M / 2 \mathop{\rm ln} ( \sqrt {2 } + 1 ) $ cannot be improved on for the entire class $ Z _ {M} $[3].

References

[1]	A. Zygmund, "Smooth functions" Duke Math. J. , 12 : 1 (1945) pp. 47–76 ((Also: Selected papers of Antoni Zygmund, Vol. 2, Kluwer, 1989, pp. 184–213.))
[2]	S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian)
[3]	A.V. Efimov, "Estimation of the modules of continuity of functions of class 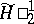" Izv. Akad. Nauk. SSSR Ser. Mat. , 21 : 2 (1957) pp. 283–288 (In Russian)

Comments

The quantity

$$ \omega _ {f} ^ {*} ( h) = \sup _ { x } \sup _ {| \delta | \leq n } \ | f( x+ \delta ) - 2f( x) + f( x- \delta ) | , $$

for a $ 2 \pi $- periodic function $ f $, is its Zygmund modulus. In terms of this, Zygmund's theorem above can also be stated as: A $ 2 \pi $- periodic function $ f $ satisfies $ E _ {n} ( f ) \leq n ^ {-} 1 A $ for some $ A $ if and only if $ \omega _ {f} ^ {*} ( h ) \leq Bh $( $ h > 0 $) for some $ B $.

References

[a1]	E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) pp. 203ff