Unramified ideal
A prime ideal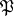 
of an algebraic number field 
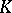(cf. also Algebraic number; Number field) lying over a prime number 
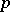such that the principal ideal 
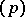has in 
a product decomposition into prime ideals of the form
 |
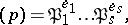where
 |
and 
. More accurately, such an ideal is called absolutely unramified. In general, let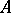 
be a Dedekind ring with field of fractions 
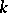, let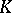 
be a finite extension of 
and let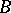 
be the integral closure of 
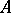in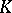 
(cf. Integral extension of a ring). A prime ideal 
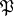of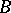 
lying over an ideal 
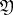of 
is unramified in the extension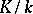 
if
 |
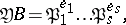where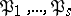 
are pairwise distinct prime ideals of 
, 
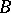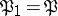and 
. If all ideals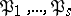 
are unramified, then one occasionally says that 
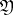remains unramified in 
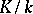. For a Galois extension 
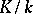, an ideal 
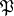of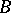 
is unramified if and only if the decomposition group of 
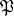in the Galois group 
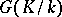is the same as the Galois group of the extension of the residue class field 
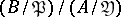. In any finite extension of algebraic number fields all ideals except finitely many are unramified.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | S. Lang, "Algebraic number theory" , Addison-Wesley (1970) |
| [3] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
Unramified ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unramified_ideal&oldid=14372