Differential equation, partial, discontinuous coefficients
A problem for partial differential equations in which the coefficients of the differential operators have discontinuities of the first kind (or jumps) on passing across certain surfaces, and where on these surfaces conjugacy conditions are given.
In the case of second-order elliptic operators the problem with discontinuous coefficients (the transmission or diffraction problem) consists in the following. Let there be given, in an arbitrary bounded open $ N $- dimensional domain $ g $ with boundary $ \Gamma $, an $ ( N - 1 ) $- dimensional surface $ \Gamma _ {1} $ which partitions $ g $ into two subdomains $ g _ {1} $ and $ g _ {2} $; in the domain $ ( g + \Gamma ) $ one poses the problem
$$ \tag{* } \left . \begin{array}{c} {L _ {l} u = f _ {l} ( x) \ \mathop{\rm in} g _ {l} , l = 1 , 2 , } \\ {\left . [ u] \right | _ {\Gamma _ {1} } = \phi ( x) ,\ \left . \left [ \frac{\partial u }{\partial v } \right ] \right | _ {\Gamma _ {1} } = \psi ( x) , } \\ {\left . u \right | _ \Gamma = \chi ( x) , } \end{array} \right \} $$
where
$$ L _ {l} u = \sum _ {i , j = 1 } ^ { N } a _ {ij} ^ {( l) } ( x) \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } + \sum _ {i = 1 } ^ { N } b _ {i} ^ {( l) } ( x) \frac{\partial u }{\partial x _ {i} } + c ^ {( l) } ( x) u $$
is a linear differential operator of elliptic type, defined in the domain $ g _ {l} $;
$$ \left . [ u] \right | _ {\Gamma _ {1} } \equiv \left . u \right | _ {x \rightarrow \Gamma _ {1} - 0 } - \left . u \right | _ {x \rightarrow \Gamma _ {1} + 0 } , $$
$$ \left . \left . \left . \left [ \frac{\partial u }{\partial v _ {1} } \right ] \right | _ {\Gamma _ {1} } \equiv \frac{ \partial u }{\partial v _ {1} } \right | _ {x \rightarrow \Gamma _ {1} - 0 } - \frac{\partial u }{\partial v _ {2} } \right | _ {x \rightarrow \Gamma _ {1} + 0 } , $$
where $ \partial / \partial v _ {l} $ is the derivative with respect to the conormal, equal to
$$ \sum _ {i , j } a _ {ij} ^ {( l) } \cos ( \mathbf n , x _ {j} ) \frac \partial {\partial x _ {i} } , $$
$ \mathbf n $ is the exterior normal to $ \Gamma _ {1} $, while the symbols $ \Gamma _ {1} - 0 $ and $ \Gamma _ {1} + 0 $ signify that the limit values are taken from the interior and the exterior sides of the surface $ \Gamma _ {1} $, respectively, with respect to the domain $ g _ {1} $, and $ f _ {l} $, $ \phi $, $ \psi $, and $ \chi $ are given functions.
It is assumed in this condition, for the sake of simplicity, that there exists only one discontinuity surface of the coefficients — the surface $ \Gamma _ {1} $.
The problem (*) is a mathematical description of stationary physical processes taking place in a domain constituted by different media, e.g. the scatter of an electromagnetic wave on some given obstacle or the propagation of heat in a layered medium.
There exists a classical solution of the problem (*) under conditions which, in the absence of discontinuity of the coefficients and when $ \phi = \psi \equiv 0 $, become the Giraud conditions for the solvability of the Dirichlet problem [3], [4], [5]. The following were studied for the problem (*): generalized solutions from $ W _ {2} ^ {p} $[1], [2]; eigen value problems and estimates for the eigen functions of the self-adjoint operators $ L _ {l} $[6], [8]; the case of degeneration in connection with Markov processes [9], [10]; and the cases with quasi-linear operators $ L _ {l} $[13]. It is possible to establish, for the problem (*), Schauder estimates [6], [7] and to develop numerical methods of their solution [11], [12]. The theory of solvability of problems involving discontinuous coefficients has been constructed for elliptic equations and systems of order $ 2m $[18], [19], [20].
The problem with discontinuous coefficients for parabolic and hyperbolic operators of the second order was also studied in detail [2], [9], [14], [15], [16], [17].
References
| [1] | O.A. Ladyzhenskaya, "On the solution of the general problem of diffraction" Dokl. Akad. Nauk SSSR , 96 : 3 (1954) pp. 433–436 (In Russian) |
| [2] | O.A. Oleinik, "Boundary value problem for linear equations of elliptic-parabolic type with discontinuous coefficients" Izv. Akad. Nauk SSSR Ser. Mat. , 25 : 1 (1961) pp. 3–20 (In Russian) |
| [3] | V.A. Il'in, I.A. Shishmarev, "The method of potentials for the problems of Dirichlet and Neumann in the case of equations with discontinuous coefficients" Sibirsk. Mat. Zh. , 2 : 1 (1961) pp. 46–58 (In Russian) |
| [4] | V.A. Il'in, "On the solvability of the Dirichlet and Neumann problems for a linear elliptic operator with discontinuous coefficients" Soviet Math. Dokl. , 2 : 2 (1961) pp. 228–230 Dokl. Akad. Nauk SSSR , 137 : 1 (1961) pp. 28–30 |
| [5] | O.A. Ladyzhenskaya, N.N. Ural'tseva, "Linear and quasilinear elliptic equations" , Acad. Press (1968) (Translated from Russian) |
| [6] | I.A. Shishmarev, "Uniform estimates of the derivatives of solutions to the Dirichlet problem and to the problem of eigenvalues for the operator 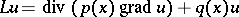 with discontinuous coefficients" Soviet Math. Dokl , 2 : 2 (1961) pp. 244–246 Dokl. Akad. Nauk SSSR , 137 : 1 (1961) pp. 45–47 with discontinuous coefficients" Soviet Math. Dokl , 2 : 2 (1961) pp. 244–246 Dokl. Akad. Nauk SSSR , 137 : 1 (1961) pp. 45–47 |
| [7] | Van Tun, "Asymptotic formulae for the solutions of boundary value problems for a general elliptic equation of the second order with discontinuous coefficients" USSR Comp. Math. Phys. , 4 : 3 (1964) pp. 257–262 Zh. Vychisl. Mat. i Mat. Fiz. , 4 : 3 (1964) pp. 577–580 |
| [8] | V.A. Il'in, "A system of classical eigenfunctions for a linear self-adjoint elliptic operator with discontinuous coefficients" Soviet Math. Dokl. , 2 : 2 (1961) pp. 264–267 Dokl. Akad. Nauk SSSR , 137 : 2 (1961) pp. 272–275 |
| [9] | I.V. Girsanov, "The solution of certain boundary problems for parabolic and elliptic equations with discontinuous coefficients" Soviet Math. Dokl. , 1 : 6 (1960) pp. 1373–1375 Dokl. Akad. Nauk SSSR , 135 : 6 (1960) pp. 1311–1313 |
| [10] | M.I. Freidlin, "The Dirichlet problem for an equation involving a small parameter and with discontinuous coefficients" Soviet Math. Dokl. , 3 : 3 (1962) pp. 767–770 Dokl. Akad. Nauk SSSR , 144 : 3 (1962) pp. 501–504 |
| [11] | A.A. Samarskii, "Proc. Fourth All-Union math. congress Leningrad, 1961" , 2 , Leningrad (1964) (In Russian) |
| [12] | A.A. Samarskii, "A priori estimate for the solution of the difference analogue of a parabolic differential equation" USSR Comp. Math. Math. Phys. , 1 : 3 (1962) pp. 487–512 Zh. Vychisl. Mat. i Mat. Fiz. , 1 : 3 (1961) pp. 441–460 |
| [13] | M.V. Borsuk, "A priori estimates and solvability of quasilinear elliptic second-order equations in a domain with nonlinear boundary and adjointness conditions" Soviet Math. Dokl. , 8 (1967) pp. 1519–1523 Dokl. Akad. Nauk SSSR , 177 : 5 (1967) pp. 991–994 |
| [14] | L.I. Kamynin, "On the theory of parabolic equations with discontinuous coefficients" , Proc. joint Soviet-American symp. on partial differential equations , Novosibirsk (1963) pp. 115–117 (In Russian) |
| [15] | L.I. Kamynin, V.N. Maslennikova, "The maximum principle for parabolic equations with continuous coefficients" Sibirsk. Mat. Zh. , 2 : 3 (1961) pp. 384–399 (In Russian) |
| [16] | V.A. Il'in, "The Fourier method for a hyperbolic equation with discontinuous coefficients" Soviet Math. Dokl. , 3 : 1 (1962) pp. 12–15 Dokl. Akad. Nauk SSSR , 142 : 1 (1962) pp. 21–24 |
| [17] | Yu.V. Egorov, "Hyperbolic equations with discontinuous coefficients" Soviet Math. Dokl. , 1 : 5 (1960) pp. 1095–1098 Dokl. Akad. Nauk SSSR , 134 : 3 (1960) pp. 514–517 |
| [18] | M. Schechter, "A generalization of the problem of transmission" Ann. Scuola Norm. Sup. Pisa Sci. Fiz. Mat. , 14 (1960) pp. 207–236 |
| [19] | Ya.A. Roitberg, Z.G. Sheftel', "General boundary-value problems for elliptic equations with discontinuous coefficients" Soviet Math. Dokl. , 4 : 1 (1963) pp. 231–234 Dokl. Akad. Nauk SSSR , 148 : 5 (1963) pp. 1034–1037 |
| [20] | Ya.A. Roitberg, Z.G. Sheftel', "Green's formula and a theorem on homeomorphisms for elliptic systems" Uspekhi Mat. Nauk , 22 : 2 (1967) pp. 181–182 (In Russian) |
Comments
If in a non-linear equation a coefficient or the free term is discontinuous (or singular) for some given value of the unknown, then the corresponding boundary value problem can be formulated as a free boundary problem (see Differential equation, partial, free boundaries).
Example.
The equation
$$ \tag{a1 } u _ {t} - u _ {xx} + H ( u) = 0 , $$
$ H ( u) = 1 $ for $ u \neq 0 $, $ H ( u) = 0 $ otherwise, is often referred to as the oxygen diffusion-consumption equation [a1]. The initial boundary value problem for (a1) can be alternatively formulated as the problem of finding a curve $ x = s ( t) $ and a function $ u ( x , t ) $ satisfying $ u _ {t} - u _ {xx} + 1 = 0 $ for $ 0 < x < s ( t) $, $ t \neq 0 $, with the conditions $ u = u _ {x} = 0 $ on the free boundary $ x = s ( t) $.
References
| [a1] | J. Crank, R.S. Gupta, "A moving boundary problem arising from the diffusion of oxygen in absorbing tissue" J. Inst. Math. Appl. , 10 (1972) pp. 19–33 |
| [a2] | G.I. Eskin, "The conjugacy problem for equations of principal type with two independent variables" Trans. Moscow Math. Soc. , 21 (1970) pp. 263–316 Tr. Moskov. Mat. Obshch. , 21 (1970) pp. 245–292 |
| [a3] | O.A. Ladyzhenskaya, V.A. Solonnikov, N.N. Ural'tseva, "Linear and quasilinear equations of parabolic type" , Amer. Math. Soc. (1968) (Translated from Russian) |
Differential equation, partial, discontinuous coefficients. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_equation,_partial,_discontinuous_coefficients&oldid=14319