Semi-continuous mapping
upper (lower)
A mapping 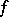 from a topological space
from a topological space 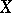 into a partially ordered set
into a partially ordered set 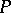 such that
such that
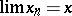 |
implies that
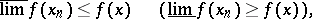 |
where  (
( ) denotes the limes superior (inferior).
) denotes the limes superior (inferior).
Comments
On a partially ordered set 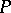 the collection consisting of
the collection consisting of 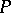 and all sets
and all sets 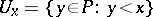 is a base for a topology on
is a base for a topology on 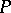 , denoted by
, denoted by 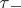 , and
, and 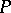 and all sets
and all sets 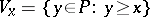 define a topology
define a topology 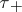 . The mapping
. The mapping 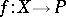 is upper semi-continuous, (u.s.c.) (respectively, lower semi-continuous (l.s.c.)) if and only if
is upper semi-continuous, (u.s.c.) (respectively, lower semi-continuous (l.s.c.)) if and only if 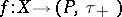 (respectively,
(respectively, 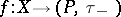 ) is continuous.
) is continuous.
In fact, upper and lower semi-continuity are usually defined only for mappings to the real line 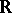 . In terms of open sets, one sees that
. In terms of open sets, one sees that 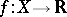 is upper (lower) semi-continuous if and only if
is upper (lower) semi-continuous if and only if 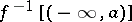 (
( ) is open for every
) is open for every  .
.
Semi-continuity is also defined for set-valued mappings. A mapping 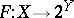 is upper (lower) semi-continuous if for every open subset
is upper (lower) semi-continuous if for every open subset 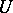 of
of 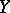 the set
the set 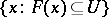 (the set
(the set 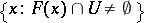 ) is open.
) is open.
Note that if a mapping 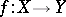 is regarded as a set-valued mapping
is regarded as a set-valued mapping 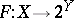 ,
, 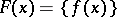 , then
, then 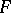 is lower semi-continuous if and only if
is lower semi-continuous if and only if 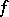 is lower semi-continuous; and
is lower semi-continuous; and 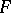 is upper semi-continuous if and only if
is upper semi-continuous if and only if 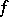 is upper semi-continuous.
is upper semi-continuous.
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
Semi-continuous mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-continuous_mapping&oldid=13587