H-cobordism
A bordism $ ( W; M _ {0} , M _ {1} ) $,
where $ W $
is a compact manifold whose boundary is the disjoint union of closed manifolds $ M _ {0} , M _ {1} $
which are deformation retracts (cf. Deformation retract) of $ W $.
The simplest example is the trivial $ h $-
cobordism
$$ ( M \times [ 0, 1]; M \times \{ 0 \} , M \times \{ 1 \} ). $$
Two manifolds $ M _ {0} $ and $ M _ {1} $ are said to be $ h $- cobordant if there is an $ h $- cobordism $ W $ joining them.
If $ ( W; M _ {0} , M _ {1} ) $ is an $ h $- cobordism such that $ W $, $ M _ {0} $, $ M _ {1} $ are simply-connected differentiable (or piecewise-linear) manifolds and $ \mathop{\rm dim} W \geq 6 $, then $ W $ is diffeomorphic (or piecewise-linearly isomorphic) to $ M _ {0} \times [ 0, 1] $: $ W \approx M _ {0} \times [ 0, 1] $ and therefore $ M _ {0} \approx M _ {1} $( the $ h $- cobordism theorem [4]). Thus, proving the isomorphism $ M _ {0} \approx M _ {1} $ reduces to providing an $ h $- cobordism, which can be achieved by methods of algebraic topology. For this reason, this theorem is basic in passing from the homotopy classification of simply-connected manifolds to their classification up to a diffeomorphism (or a piecewise-linear isomorphism). Thus, if $ W ^ {n} $, $ n \geq 6 $, is a compact differentiable manifold with simply-connected boundary, then it is diffeomorphic to the disc $ D ^ {n} $. If $ M ^ {n} $, $ n \geq 5 $, is a manifold that is homotopy equivalent to the sphere $ S ^ {n} $, then it is homeomorphic (and even piecewise-linearly isomorphic) to $ S ^ {n} $( the generalized Poincaré conjecture).
The $ h $- cobordism theorem allows one to classify the differentiable structures on the sphere $ S ^ {n} $, $ n \geq 5 $[6], and also on the homotopy type of an arbitrary closed simply-connected manifold $ M ^ {n} $, $ n \geq 5 $[1].
In the case of an $ h $- cobordism $ ( W; M _ {0} , M _ {1} ) $ with $ \pi _ {1} W \neq \{ 1 \} $ there is, in general, no diffeomorphism from $ W $ to $ M _ {0} \times [ 0, 1] $.
All $ h $- cobordisms $ ( W; M _ {0} , M _ {1} ) $ with $ \mathop{\rm dim} W \geq 6 $ and $ M _ {0} $ fixed are classified by a certain Abelian group, namely the Whitehead group $ \mathop{\rm Wh} \pi _ {1} $ of the group $ \pi _ {1} M _ {0} $. Corresponding to a given $ h $- cobordism is an element of $ \mathop{\rm Wh} \pi _ {1} $ that is an invariant of the pair $ ( W, M _ {0} ) $; it is denoted by $ \tau ( W, M _ {0} ) $ and is called the torsion (sometimes the Whitehead torsion) of the given $ h $- cobordism. If $ \tau ( W, M _ {0} ) = 0 $( or, equivalently, $ \tau ( W, M _ {1} ) = 0 $), then the $ h $- cobordism is called an $ s $- cobordism. If $ ( W; M _ {0} , M _ {1} ) $ is an $ h $- cobordism such that $ \mathop{\rm dim} W \geq 6 $, then $ \tau ( W, M _ {0} ) $ vanishes if and only if $ W \approx M _ {0} \times [ 0, 1] $( the $ s $- cobordism theorem). The $ h $- cobordism theorem is a special case of this theorem in view of the fact that $ \mathop{\rm Wh} \{ 1 \} = 0 $. The $ s $- cobordism theorem is also true for topological manifolds [9].
For an $ h $- cobordism $ ( W; M _ {0} , M _ {1} ) $, the torsion $ \tau ( W, M _ {1} ) $ is defined along with $ \tau ( W, M _ {0} ) $; if the given $ h $- cobordism is orientable, then $ \tau ( W, M _ {0} ) = (- 1) ^ {n - 1 } \tau ^ {*} ( W, M _ {1} ) $, where $ n = \mathop{\rm dim} W $ and the element $ \tau ^ {*} $ is conjugate to $ \tau $ in the group $ \mathop{\rm Wh} \pi _ {1} $. In particular, if $ \pi _ {1} $ is finite and Abelian, $ \tau ^ {*} = \tau $.
If two $ h $- cobordisms $ ( W; M _ {0} , M _ {1} ) $ and $ ( W ^ \prime ; M _ {1} , M _ {2} ) $ are glued along $ M _ {1} $ to the $ h $- cobordism $ ( W \cup W ^ \prime ; M _ {0} , M _ {1} ) $, then
$$ \tau ( W \cup W ^ \prime , M _ {0} ) = \ \tau ( W, M _ {0} ) + \tau ( W ^ \prime , M _ {1} ). $$
If two copies of $ W $ are glued along $ M _ {1} $, where $ \mathop{\rm dim} W $ is odd and $ \pi _ {1} = \mathbf Z _ {5} $, then one obtains an $ h $- cobordism $ ( 2W; M _ {0} , M _ {0} ^ \prime ) $, where $ M _ {0} = M _ {0} ^ \prime $ when there is no diffeomorphism from $ W $ to $ M _ {0} \times [ 0, 1] $, that is, when $ M _ {0} \approx M _ {1} $ does not imply that the $ h $- cobordism connecting them is trivial.
If $ M _ {0} $ is a closed connected manifold and $ \mathop{\rm dim} M _ {0} \geq 5 $, then there exists for any $ \tau \in \mathop{\rm Wh} \pi _ {1} M _ {0} $ an $ h $- cobordism $ ( W; M _ {0} , M _ {1} ) $ with $ \tau ( W, M _ {0} ) = \tau $. If $ ( W; M _ {0} , M _ {1} ) $ and $ ( W ^ \prime ; M _ {0} , M _ {1} ^ \prime ) $( with $ \mathop{\rm dim} W \geq 6 $) have the same torsion $ \tau ( W, M _ {0} ) = \tau ( W ^ \prime , M _ {0} ) $, then $ W \approx W ^ \prime $ relative to $ M _ {0} $. When $ \mathop{\rm dim} M _ {0} $ is even and $ \pi _ {1} M _ {0} $ is finite, there is a finite set of distinct manifolds that are $ h $- cobordant with $ M _ {0} $. This is not the case when $ \mathop{\rm dim} M _ {0} $ is odd.
If two homotopy-equivalent manifolds $ M _ {1} $ and $ M _ {2} $ are imbedded in $ \mathbf R ^ {N} $, with $ N $ sufficiently large, and their normal bundles are trivial, then $ M _ {1} \times S ^ {N} $ and $ M _ {2} \times S ^ {N} $ are $ h $- cobordant. If, moreover, $ M _ {1} $ and $ M _ {2} $ are of the same simple homotopy type, that is, if the torsion of this homotopy equivalence vanishes, then $ M _ {1} \times S ^ {N} \approx M _ {2} \times S ^ {N} $.
If $ ( W; M _ {0} , M _ {1} ) $ is an $ h $- cobordism and $ P $ is a closed manifold, then there is an $ h $- cobordism $ ( W \times P; M _ {0} \times P, M _ {1} \times P) $ with $ \tau ( W \times P, M _ {0} \times P) = \tau ( W, M _ {0} ) \chi ( P) $, where $ \chi ( P) $ is the Euler characteristic of $ P $. If $ \mathop{\rm dim} W \geq 5 $ and $ P = S ^ {1} $, then
$$ W \times S ^ {1} \approx \ M _ {0} \times S ^ {1} \times [ 0, 1] \approx \ M _ {1} \times S ^ {1} \times [ 0, 1]. $$
In particular, $ M _ {0} \times S ^ {1} \approx M _ {1} \times S ^ {1} $; furthermore, two closed manifolds $ M _ {0} $ and $ M _ {1} $ of the same dimension $ \geq 5 $ are $ h $- cobordant if and only if $ M _ {0} \times \mathbf R ^ {1} \approx M _ {1} \times \mathbf R ^ {1} $.
The $ h $- cobordism structure has not been completely elucidated for $ n < 6 $( 1978). Thus there is the following negative result [8]: There exists an $ h $- cobordism $ ( W; T ^ {4} , T ^ {4} ) $, where $ T ^ {4} $ is the four-dimensional torus, for which there is no diffeomorphism from $ W $ to $ T ^ {4} \times [ 0, 1] $; since $ \mathop{\rm Wh} \pi _ {1} T ^ {4} = 0 $, this means that the $ s $- cobordism theorem fails for $ n = 5 $.
References
| [1] | S.P. Novikov, "Homotopy-equivalent smooth manifolds I" Izv. Akad. Nauk SSSR Ser. Mat. , 28 : 2 (1964) pp. 365–474 (In Russian) |
| [2] | J. Milnor, "Lectures on the 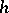 -cobordism theorem" , Princeton Univ. Press (1965) -cobordism theorem" , Princeton Univ. Press (1965) |
| [3] | J. Milnor, "Whitehead torsion" Bull. Amer. Math. Soc. , 72 (1966) pp. 358–462 |
| [4] | S. Smale, "On the structure of manifolds" Amer. J. Math. , 84 (1962) pp. 387–399 |
| [5] | J. Milnor, "Sommes des variétés différentiables et structures différentiables des sphères" Bull. Soc. Math. France , 87 (1959) pp. 439–444 |
| [6] | M. Kervaire, J. Milnor, "Groups of homotopy spheres I" Ann. of Math. (2) , 77 (1963) pp. 504–537 |
| [7] | B. Mazur, "Relative neighbourhoods and the theorems of Smale" Ann. of Math. , 77 (1963) pp. 232–249 |
| [8] | L.C. Siebenmann, "Disruption of low-dimensional handlebody theory by Rohlin's theorem" J.C. Cantrell (ed.) C.H. Edwards jr. (ed.) , Topology of manifolds , Markham (1969) pp. 57–76 |
| [9] | R. Kirby, L. Siebenmann, "On the triangulation of manifolds and the Hauptvermutung" Bull. Amer. Math. Soc. , 75 (1969) pp. 742–749 |
| [10] | M.A. Kervaire, "Le théorème de Barden–Mazur–Stallings" M.A. Kervaire (ed.) G. de Rham (ed.) S. Maumary (ed.) , Torsion et type simple d'homotopie , Lect. notes in math. , 48 , Springer (1967) pp. 83–95 |
| [11] | R. Thom, "Les classes caractéristiques de Pontryagin des variétés triangulées" , Symp. Internac. Topol. Algebr. , Univ. Nac. Aut. Mexico & UNESCO (1958) pp. 54–67 |
| [12] | C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972) |
Comments
For the generalized Poincaré conjecture see also [a1].
References
| [a1] | S. Smale, "Generalized Poincaré's conjecture in dimensions greater than four" Ann. of Math. (2) , 74 (1961) pp. 391–406 |
H-cobordism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=H-cobordism&oldid=11321