Spinor representation

spin representation

The simplest faithful linear representation (cf. Faithful representation; Linear representation) of the spinor group $ \mathop{\rm Spin} _ {n} ( Q) $, or the linear representation of the corresponding even Clifford algebra $ C ^ {+} = C ^ {+} ( Q) $( see Spinor group; $ Q $ is a quadratic form). If the ground field $ K $ is algebraically closed, then the algebra $ C ^ {+} $ is isomorphic to the complete matrix algebra $ M _ {2 ^ {m} } ( K) $( where $ n = 2 m + 1 $) or to the algebra $ M _ {2 ^ {m-1} } ( K) \oplus M _ {2 ^ {m-1} } ( K) $( where $ n = 2 m $). Therefore there is defined a linear representation $ \rho $ of the algebra $ C ^ {+} $ on the space of dimension $ 2 ^ {m} $ over $ K $; this representation is called a spinor representation. The restriction of $ \rho $ to $ \mathop{\rm Spin} _ {n} ( Q) $ is called the spinor representation of $ \mathop{\rm Spin} _ {n} ( Q) $. For odd $ n $, the spinor representation is irreducible, and for even $ n $ it splits into the direct sum of two non-equivalent irreducible representations $ \rho ^ \prime $ and $ \rho ^ {\prime\prime} $, which are called half-spin (or) representations. The elements of the space of the spinor representation are called spinors, and those of the space of the half-spinor representation half-spinors. The spinor representation of the spinor group $ \mathop{\rm Spin} _ {n} $ is self-dual for any $ n \geq 3 $, whereas the half-spinor representations $ \rho ^ \prime $ and $ \rho ^ {\prime\prime} $ of the spinor group $ \mathop{\rm Spin} _ {2m} $ are self-dual for even $ m $ and dual to one another for odd $ m $. The spinor representation of $ \mathop{\rm Spin} _ {n} $ is faithful for all $ n \geq 3 $, while the half-spinor representations of $ \mathop{\rm Spin} _ {2m} $ are faithful for odd $ m $, but have a kernel of order two when $ m $ is even.

For a quadratic form $ Q $ on a space $ V $ over some subfield $ k \subset K $, the spinor representation is not always defined over $ k $. However, if the Witt index of $ Q $ is maximal, that is, equal to $ [ n / 2 ] $( in particular, if $ k $ is algebraically closed), then the spinor and half-spinor representations are defined over $ k $. In this case these representations can be described in the following way if $ \mathop{\rm char} k \neq 2 $( see [1]). Let $ L $ and $ M $ be $ k $- subspaces of the $ k $- space $ V $ that are maximal totally isotropic (with respect to the symmetric bilinear form on $ V $ associated with $ Q $) and let $ L \cap M = 0 $. Let $ C _ {L} $ be the subalgebra of the Clifford algebra $ C = C ( Q) $ generated by the subspace $ L \subset V $, and let $ e _ {M} \in C $ be the product of $ m $ vectors forming a $ k $- basis of $ M $. If $ n $ is even, $ n = 2m $, then the spinor representation is realized in the left ideal $ C e _ {M} $ and acts there by left translation: $ \rho ( s) x = s x $( $ s \in C ^ {+} $, $ x \in C e _ {M} $). Furthermore, the mapping $ x \mapsto x e _ {M} $ defines an isomorphism of vector spaces $ C _ {L} \rightarrow C e _ {M} $ that enables one to realize the spinor representation in $ C _ {L} $, which is naturally isomorphic to the exterior algebra over $ L $. The half-spinor representations $ \rho ^ \prime $ and $ \rho ^ {\prime\prime} $ are realized in the $ 2 ^ {m-} 1 $- dimensional subspaces $ C _ {L} \cap C ^ {+} $ and $ C _ {L} \cap C ^ {-} $.

If $ n $ is odd, then $ V $ can be imbedded in the $ ( n + 1 ) $- dimensional vector space $ V _ {1} = V \oplus k \epsilon $ over $ k $. One defines a quadratic form $ Q _ {1} $ on $ V _ {1} $ by putting $ Q _ {1} ( v + \epsilon ) = Q ( v) - \lambda ^ {2} $ for all $ v \in V $ and $ \lambda \in k $. $ Q _ {1} $ is a non-degenerate quadratic form of maximal Witt index defined over $ k $ on the even-dimensional vector space $ V _ {1} $. The spinor representation of $ C ^ {+} ( Q) $( or of $ \mathop{\rm Spin} _ {n} ( Q) $) is obtained by restricting any of the half-spinor representations of $ C ^ {+} ( Q _ {1} ) $( or of $ \mathop{\rm Spin} _ {n+} 1 ( Q _ {1} ) $) to the subalgebra $ C ^ {+} ( Q) $( or $ \mathop{\rm Spin} _ {n} ( Q) $, respectively).

The problem of classifying spinors has been solved when $ 3 \leq n \leq 14 $ and $ k $ is an algebraically closed field of characteristic 0 (see [4], [8], [9]). The problem consists of the following: 1) describe the orbits of $ \rho ( \mathop{\rm Spin} _ {n} ) $ in the spinor space by giving a representative of each orbit; 2) calculate the stabilizers in $ \mathop{\rm Spin} _ {n} $ of each of these representatives; and 3) describe the algebra of invariants of the linear group $ \rho ( \mathop{\rm Spin} _ {n} ) $.

The existence of spinor and half-spinor representations of the Lie algebra $ \mathfrak s \mathfrak p _ {n} $ of $ \mathop{\rm Spin} _ {n} $ was discovered by E. Cartan in 1913, when he classified the finite-dimensional representations of simple Lie algebras [6]. In 1935, R. Brauer and H. Weyl described spinor and half-spinor representations in terms of Clifford algebras [5]. P. Dirac [3] showed how spinors could be used in quantum mechanics to describe the rotation of an electron.

References

[1]	N. Bourbaki, "Algèbre" , Eléments de mathématiques , Hermann (1970) pp. Chapt. II. Algèbre linéaire MR0274237 Zbl 0211.02401
[2]	H. Weyl, "Classical groups, their invariants and representations" , Princeton Univ. Press (1946) (Translated from German) MR0000255 Zbl 1024.20502
[3]	P.A.M. Dirac, "Principles of quantum mechanics" , Clarendon Press (1958) MR2303789 MR0116921 MR0023198 MR1522388 Zbl 0080.22005
[4]	V.L. Popov, "Classification of spinors of dimension fourteen" Trans. Moscow Math. Soc. , 1 (1980) pp. 181–232 Trudy Moskov. Mat. Obshch. , 37 (1978) pp. 173–217 MR0514331 Zbl 0443.20038
[5]	R. Brauer, H. Weyl, "Spinors in -dimensions" Amer. J. Math. , 57 : 2 (1935) pp. 425–449 MR1507084
[6]	E. Cartan, "Les groupes projectifs qui ne laissant invariante aucune multiplicité plane" Bull. Soc. Math. France , 41 (1913) pp. 53–96
[7]	C. Chevalley, "The algebraic theory of spinors" , Columbia Univ. Press (1954) MR0060497 Zbl 0057.25901
[8]	V. Gatti, E. Viniberghi, "Spinors in 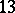-dimensional space" Adv. Math. , 30 : 2 (1978) pp. 137–155
[9]	J.I. Igusa, "A classification of spinors up to dimension twelve" Amer. J. Math. , 92 : 4 (1970) pp. 997–1028 MR0277558 Zbl 0217.36203