Difference between revisions of "Rational tangles"
m (adding ZBL links) |
|||
| Line 6: | Line 6: | ||
Out of 12 formulas, 10 were replaced by TEX code.--> | Out of 12 formulas, 10 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|done}} |
| − | A family of $2$-tangles (cf. [[ | + | |
| + | A family of $2$-tangles (cf. [[Tangle]]) classified by J.H. Conway. The $2$-tangle of Fig. a1 is called a rational tangle with Conway notation $T ( a _ { 1 } , \dots , a _ { n } )$. It is a rational $p / q$-tangle if | ||
\begin{equation*} \frac { p } { q } = a _ { n } + \frac { 1 } { a _ { n - 1} + \ldots + \frac { 1 } { a_ { 1 } } }. \end{equation*} | \begin{equation*} \frac { p } { q } = a _ { n } + \frac { 1 } { a _ { n - 1} + \ldots + \frac { 1 } { a_ { 1 } } }. \end{equation*} | ||
| Line 25: | Line 26: | ||
====References==== | ====References==== | ||
| − | * {{Ref|a1}} J.H. Conway, "An enumeration of knots and links" | + | * {{Ref|a1}} J.H. Conway, "An enumeration of knots and links" J. Leech (ed.), ''Computational Problems in Abstract Algebra'', Pergamon Press (1969) pp. 329–358 {{ZBL|0202.54703}} |
| − | * {{Ref|a2}} A. Kawauchi, "A survey of knot theory" , Birkhäuser | + | * {{Ref|a2}} A. Kawauchi, "A survey of knot theory", Birkhäuser (1996) {{ZBL|0861.57001}} |
| − | + | {{OldImage}} | |
Latest revision as of 07:50, 25 November 2023
A family of $2$-tangles (cf. Tangle) classified by J.H. Conway. The $2$-tangle of Fig. a1 is called a rational tangle with Conway notation $T ( a _ { 1 } , \dots , a _ { n } )$. It is a rational $p / q$-tangle if
\begin{equation*} \frac { p } { q } = a _ { n } + \frac { 1 } { a _ { n - 1} + \ldots + \frac { 1 } { a_ { 1 } } }. \end{equation*}
The fraction $p / q$ is called the slope of the tangle and can be identified with the slope of the meridian disc of the solid torus that is the branched double covering of the rational tangle.

Figure: r130030a
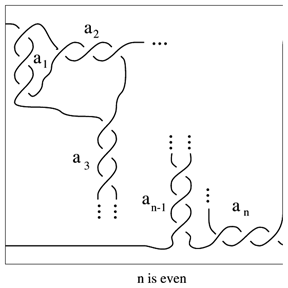
Figure: r130030b
Conway proved that two rational tangles are ambient isotopic (with boundary fixed) if and only if their slopes are equal. A rational $n$-tangle (also called an $n$-bridge $n$-tangle) is an $n$-tangle that can be obtained from the identity tangle by a finite number of additions of a single crossing.
References
- [a1] J.H. Conway, "An enumeration of knots and links" J. Leech (ed.), Computational Problems in Abstract Algebra, Pergamon Press (1969) pp. 329–358 Zbl 0202.54703
- [a2] A. Kawauchi, "A survey of knot theory", Birkhäuser (1996) Zbl 0861.57001
Rational tangles. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_tangles&oldid=54668