Difference between revisions of "Basic set"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
|||
| Line 1: | Line 1: | ||
''of a linear system'' | ''of a linear system'' | ||
| − | The set of points of an algebraic variety (or of a scheme) | + | The set of points of an algebraic variety (or of a scheme) $X$ which belong to all the divisors of the movable part of the given linear system $L$ on $X$. |
Example. Let | Example. Let | ||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> "Algebraic surfaces" ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965) (In Russian) {{MR|}} {{ZBL|0154.33002}} {{ZBL|0154.21001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> "Algebraic surfaces" ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965) (In Russian) {{MR|}} {{ZBL|0154.33002}} {{ZBL|0154.21001}} </TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|want}} | ||
Revision as of 16:42, 1 November 2023
of a linear system
The set of points of an algebraic variety (or of a scheme) $X$ which belong to all the divisors of the movable part of the given linear system $L$ on $X$.
Example. Let
 |
be a pencil of  -th order curves on the projective plane. The basic set of this pencil then consists of the set of common zeros of the forms
-th order curves on the projective plane. The basic set of this pencil then consists of the set of common zeros of the forms 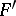 and
and 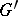 , where
, where
 |
and 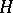 is the greatest common divisor of the forms
is the greatest common divisor of the forms 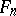 and
and 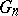 .
.
If 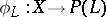 is the rational mapping defined by
is the rational mapping defined by 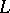 , then the basic set of
, then the basic set of 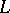 is the set of points of indeterminacy of
is the set of points of indeterminacy of 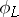 . A basic set has the structure of a closed subscheme
. A basic set has the structure of a closed subscheme 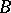 in
in 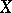 , defined as the intersection of all divisors of the movable part of the linear system. The removal of the points of indeterminacy of
, defined as the intersection of all divisors of the movable part of the linear system. The removal of the points of indeterminacy of 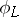 can be reduced to the trivialization of the coherent sheaf of ideals defining the subscheme
can be reduced to the trivialization of the coherent sheaf of ideals defining the subscheme 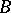 (cf. Birational geometry).
(cf. Birational geometry).
For any linear system without fixed components 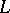 on a smooth projective surface
on a smooth projective surface 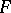 there exists an integer
there exists an integer 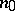 such that if
such that if 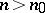 , then the basic set of the complete linear system
, then the basic set of the complete linear system 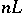 is empty (Zariski's theorem). This is not true in the multi-dimensional case.
is empty (Zariski's theorem). This is not true in the multi-dimensional case.
References
| [1] | "Algebraic surfaces" Trudy Mat. Inst. Steklov. , 75 (1965) (In Russian) Zbl 0154.33002 Zbl 0154.21001 |
| [2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
Basic set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Basic_set&oldid=54206