Difference between revisions of "Kappa"
From Encyclopedia of Mathematics
(TeX) |
m (svg image) |
||
| Line 8: | Line 8: | ||
$$\rho=a\operatorname{cotan}\phi.$$ | $$\rho=a\operatorname{cotan}\phi.$$ | ||
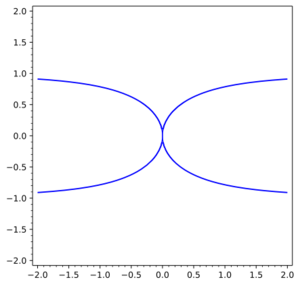
| − | + | [[File:Kappa curve.svg|center|300px|Kappa curve for a=1]] | |
| − | |||
| − | |||
The origin is a nodal point with coincident tangents $x=0$ (see Fig.). The asymptotes are the lines $y=\pm a$. It is related to the so-called nodes (cf. [[Node|Node]] in geometry). | The origin is a nodal point with coincident tangents $x=0$ (see Fig.). The asymptotes are the lines $y=\pm a$. It is related to the so-called nodes (cf. [[Node|Node]] in geometry). | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR> |
| − | + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)</TD></TR></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 08:22, 17 March 2023
A plane algebraic curve of order four whose equation in Cartesian rectangular coordinates has the form
$$(x^2+y^2)y^2=a^2x^2;$$
and in polar coordinates:
$$\rho=a\operatorname{cotan}\phi.$$
The origin is a nodal point with coincident tangents $x=0$ (see Fig.). The asymptotes are the lines $y=\pm a$. It is related to the so-called nodes (cf. Node in geometry).
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
How to Cite This Entry:
Kappa. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kappa&oldid=52746
Kappa. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kappa&oldid=52746
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article