Lie algebra, semi-simple

A Lie algebra that has no non-zero solvable ideals (see Lie algebra, solvable). Henceforth finite-dimensional semi-simple Lie algebras over a field $ k $ of characteristic 0 are considered (for semi-simple Lie algebras over a field of non-zero characteristic see Lie algebra).

The fact that a finite-dimensional Lie algebra $ \mathfrak g $ is semi-simple is equivalent to any of the following conditions:

1) $ \mathfrak g $ does not contain non-zero Abelian ideals;

2) the Killing form of $ \mathfrak g $ is non-singular (Cartan's criterion);

3) $ \mathfrak g $ splits into the direct sum of non-Abelian simple ideals;

4) every finite-dimensional linear representation of $ \mathfrak g $ is completely reducible (in other words: every finite-dimensional $ \mathfrak g $ -module is semi-simple);

5) the one-dimensional cohomology of $ \mathfrak g $ with values in an arbitrary finite-dimensional $ \mathfrak g $ -module is trivial.

Any ideal and any quotient algebra of a semi-simple Lie algebra is also semi-simple. The decomposition of a semi-simple Lie algebra mentioned in condition 3) is unique. A special case of condition 5) is the following assertion: All derivations of a semi-simple Lie algebra are inner. The property of a Lie algebra of being semi-simple is preserved by both extensions and restrictions of the ground field.

Let $ \mathfrak g $ be a semi-simple Lie algebra over an algebraically closed field $ k $ . The adjoint representation maps $ \mathfrak g $ isomorphically onto the linear Lie algebra $ \mathop{\rm ad}\nolimits \ \mathfrak g $ , which is the Lie algebra of the algebraic group $ \mathop{\rm Aut}\nolimits \ \mathfrak g $ of all automorphisms of $ \mathfrak g $ and is therefore an algebraic Lie algebra (cf. Lie algebra, algebraic). An element $ X \in \mathfrak g $ is said to be semi-simple (nilpotent) if $ \mathop{\rm ad}\nolimits \ X $ is semi-simple (respectively, nilpotent). This property of an element $ X $ is preserved by any homomorphism of $ \mathfrak g $ into another semi-simple Lie algebra. The identity component $ ( \mathop{\rm Aut}\nolimits \ \mathfrak g ) ^{0} $ coincides with the group of inner automorphisms of $ \mathfrak g $ , that is, it is generated by the automorphisms of the form $ \mathop{\rm exp}\nolimits ( \mathop{\rm ad}\nolimits \ X ) $ , $ X \in \mathfrak g $ .

In the study of semi-simple Lie algebras over an algebraically closed field $ k $ an important role is played by the roots of a semi-simple Lie algebra, which are defined as follows. Let $ \mathfrak h $ be a Cartan subalgebra of $ \mathfrak g $ . For a non-zero linear function $ \alpha \in \mathfrak h ^ \ast $ , let $ \mathfrak g _ \alpha $ denote the linear subspace of $ \mathfrak g $ given by the condition $$ \mathfrak g _ \alpha = \{ {X \in \mathfrak g} : {[ H ,\ X ] = \alpha (H) X , H \in \mathfrak h} \} . $$ If $ \mathfrak g _ \alpha \neq 0 $ , then $ \alpha $ is called a root of $ \mathfrak g $ with respect to $ \mathfrak h $ . The set $ \Sigma $ of all non-zero roots is called the root system, or system of roots, of $ \mathfrak g $ . One has the root decomposition $$ \mathfrak g = \mathfrak h + \sum _ {\alpha \in \Sigma} \mathfrak g _ \alpha . $$ The root system and the root decomposition of a semi-simple Lie algebra have the following properties:

a) $ \Sigma $ generates $ \mathfrak h ^ \ast $ and is a reduced root system in the abstract sense (in the linear hull of $ \Sigma $ over the field of the real numbers). The system $ \Sigma $ is irreducible if and only if $ \mathfrak g $ is simple.

b) For any $ \alpha \in \Sigma $ , $$ \mathop{\rm dim}\nolimits \ \mathfrak g _ \alpha = \mathop{\rm dim}\nolimits \ [ \mathfrak g _ \alpha ,\ \mathfrak g _ {- \alpha} ] = 1 . $$ There is a unique element $ H _ \alpha \in [ \mathfrak g _ \alpha ,\ \mathfrak g _ {- \alpha} ] $ such that $ \alpha ( H _ \alpha ) = 2 $ .

c) For every non-zero $ X _ \alpha \in \mathfrak g _ \alpha $ there is a unique $ Y _ \alpha \in \mathfrak g _ {- \alpha} $ such that $ [ X _ \alpha ,\ Y _ \alpha ] = H _ \alpha $ , and $$ [ H _ \alpha ,\ X _ \alpha ] = 2 X _ \alpha \textrm{ and } [ H _ \alpha ,\ Y _ \alpha ] = - 2 Y _ \alpha . $$ Moreover, $$ \beta ( H _ \alpha ) = \frac{2 ( \alpha ,\ \beta )}{( \alpha ,\ \alpha )} , \alpha ,\ \beta \in \Sigma , $$ where $ ( \ ,\ ) $ is the scalar product induced by the Killing form.

d) If $ \alpha ,\ \beta \in \Sigma $ and $ \alpha + \beta \neq 0 $ , then $ \mathfrak g _ \alpha $ and $ \mathfrak g _ \beta $ are orthogonal with respect to the Killing form and $ [ \mathfrak g _ \alpha ,\ \mathfrak g _ \beta ] = \mathfrak g _ {\alpha + \beta} $ .

A basis $ \{ \alpha _{1} \dots \alpha _{n} \} $ of the root system $ \Sigma $ is also called a system of simple roots of the algebra $ \mathfrak g $ . Let $ \Sigma _{+} $ be the system of positive roots with respect to the given basis and let $ X _ {- \alpha} = Y _ \alpha $ $ ( \alpha \in \Sigma _{+} ) $ . Then the elements $$ H _ {\alpha _{1}} \dots H _ {\alpha _{k}} ,\ X _ \alpha ( \alpha \in \Sigma ) $$ form a basis of $ \mathfrak g $ , called a Cartan basis. On the other hand, the elements $$ X _ {\alpha _{i}} , X _ {- \alpha _{i}} ( i = 1 \dots n ) $$ form a system of generators of $ \mathfrak g $ , and the defining relations have the following form: $$ [ [ X _ {\alpha _{i}} ,\ X _ {- \alpha _{i}} ] ,\ X _ {\alpha _{j}} ] = n ( i ,\ j ) X _ {\alpha _{j}} , $$ $$ [ [ X _ {\alpha _{i}} ,\ X _ {- \alpha _{i}} ] ,\ X _ {- \alpha _{j}} ] = - n ( i ,\ j ) X _ {\alpha _{j}} , $$ $$ ( \mathop{\rm ad}\nolimits \ X _ {\alpha _{i}} ) ^ {1 - n ( i ,\ j )} X _ {\alpha _{j}} = 0 , $$ $$ ( \mathop{\rm ad}\nolimits \ X _ {- \alpha _{i}} ) ^ {1 - n ( i ,\ j )} X _ {- \alpha _{j}} = 0 . $$ Here $ i ,\ j = 1 \dots n $ and $$ n ( i ,\ j ) = \alpha _{j} ( H _{i} ) = \frac{2 ( \alpha _{i} ,\ \alpha _{j} )}{( \alpha _{j} ,\ \alpha _{j} )} . $$ Property d) implies that $$ [ X _ \alpha ,\ X _ \beta ] = \left \{ \begin{array}{ll} N _ {\alpha , \beta} X _ {\alpha + \beta} & \textrm{ if } \alpha + \beta \in \Sigma , \\ 0 & \textrm{ if } \alpha + \beta \notin \Sigma , \\ \end{array} \right .$$where $ N _ {\alpha , \beta} \in k $ . The elements $ X _ \alpha $ $ ( \alpha \in \Sigma _{+} ) $ can be chosen in such a way that $$ N _ {\alpha , \beta} = - N _ {- \alpha , - \beta} \textrm{ and } N _ {\alpha , \beta} = \pm ( p + 1 ) , $$ where $ p $ is the largest integer such that $ \beta - p \alpha \in \Sigma $ . The corresponding Cartan basis is called a Chevalley basis. The structure constants of $ \mathfrak g $ in this basis are integers, which makes it possible to associate with $ \mathfrak g $ Lie algebras and algebraic groups (see Chevalley group) over fields of arbitrary characteristic. If $ k = \mathbf C $ , then the linear hull over $ \mathbf R $ of the vectors $$ i H _ \alpha , X _ \alpha - X _ {- \alpha} , i ( X _ \alpha + X _ {- \alpha} ) \quad ( \alpha \in \Sigma _{+} ) $$ is a compact real form of $ \mathfrak g $ .

A semi-simple Lie algebra is defined up to an isomorphism by its Cartan subalgebra and the corresponding root system. More precisely, if $ \mathfrak g _{1} $ and $ \mathfrak g _{2} $ are semi-simple Lie algebras over $ k $ , $ \mathfrak h _{1} $ and $ \mathfrak h _{2} $ are their Cartan subalgebras and $ \Sigma _{1} $ and $ \Sigma _{2} $ are the corresponding root systems, then every isomorphism $ \mathfrak h _{1} \rightarrow \mathfrak h _{2} $ that induces an isomorphism of the root systems $ \Sigma _{1} $ and $ \Sigma _{2} $ can be extended to an isomorphism $ \mathfrak g _{1} \rightarrow \mathfrak g _{2} $ . On the other hand, any reduced root system can be realized as the root system of some semi-simple Lie algebra. Thus, the classification of semi-simple Lie algebras (respectively, simple non-Abelian Lie algebras) over an algebraically closed field $ k $ essentially coincides with the classification of reduced root systems (respectively, irreducible reduced root systems).

Simple Lie algebras that correspond to root systems of types $ A $ – $ D $ are said to be classical and have the following form.

Type $ A _{n} $ , $ n \geq 1 $ . $ \mathfrak g = \mathfrak s \mathfrak l ( n + 1 ,\ k ) $ , the algebra of linear transformations of the space $ k ^{n+1} $ with trace 0; $ \mathop{\rm dim}\nolimits \ \mathfrak g = n ( n + 2 ) $ .

Type $ B _{n} $ , $ n \geq 2 $ . $ \mathfrak g = \mathfrak s \mathfrak o ( 2 n + 1 ,\ k ) $ , the algebra of linear transformations of the space $ k ^{2n+1} $ that are skew-symmetric with respect to a given non-singular symmetric bilinear form; $ \mathop{\rm dim}\nolimits \ \mathfrak g = n ( 2 n + 1 ) $ .

Type $ C _{n} $ , $ n \geq 3 $ . $ \mathfrak g = \mathfrak s \mathfrak p ( n ,\ k ) $ , the algebra of linear transformations of the space $ k ^{2n} $ that are skew-symmetric with respect to a given non-singular skew-symmetric bilinear form; $ \mathop{\rm dim}\nolimits \ \mathfrak g = n ( 2 n + 1 ) $ .

Type $ D _{n} $ , $ n \geq 4 $ . $ \mathfrak g = \mathfrak s \mathfrak o ( 2 n ,\ k ) $ , the algebra of linear transformations of the space $ k ^{2n} $ that are skew-symmetric with respect to a given non-singular symmetric bilinear form; $ \mathop{\rm dim}\nolimits \ \mathfrak g = n ( 2 n - 1 ) $ .

The simple Lie algebras corresponding to the root systems of types $ E _{6} $ , $ E _{7} $ , $ E _{8} $ , $ F _{4} $ , $ G _{2} $ are called special, or exceptional (see Lie algebra, exceptional).

The Cartan matrix of a semi-simple Lie algebra over an algebraically closed field also determines this algebra uniquely up to an isomorphism. The Cartan matrices of the simple Lie algebras have the following form: $$ A _{n} : \left \| \begin{array}{rrrcr} 2 &-1 & 0 &\dots & 0 \\ -1 & 2 &-1 &\dots & 0 \\ 0 &-1 & 2 &\dots & 0 \\ . & . & . &\ddots & . \\ 0 & 0 & 0 &\dots &-1 \\ 0 & 0 & 0 &\dots & 2 \\ \end{array} \right \| , $$ $$ B _{n} : \left \| \begin{array}{rrrrrr} 2 &-1 & 0 &\dots & 0 & 0 \\ -1 & 2 &-1 &\dots & 0 & 0 \\ 0 &-1 & 2 &\dots & 0 & 0 \\ . & . & . &\ddots & . & . \\ 0 & 0 & 0 &\dots & 2 &-2 \\ 0 & 0 & 0 &\dots &-1 & 2 \\ \end{array} \right \| , $$ $$ C _{n} : \left \| \begin{array}{rrrrrrr} 2 &-1 & 0 &\dots & 0 & 0 \\ -1 & 2 &-1 &\dots & 0 & 0 \\ 0 &-1 & 2 &\dots & 0 & 0 \\ . & . & . &\cdots & . & . \\ 0 & 0 & 0 &\dots & 2 &-1 \\ 0 & 0 & 0 &\dots &-2 & 2 \\ \end{array} \right \| , $$ $$ D _{n} : \left \| \begin{array}{rrrrrrrr} 2 &-1 & 0 &\dots & 0 & 0 & 0 & 0 \\ -1 & 2 &-1 &\dots & 0 & 0 & 0 & 0 \\ 0 &-1 & 2 &\dots & 0 & 0 & 0 & 0 \\ . & . & . &\ddots & . & . & . & . \\ 0 & 0 & 0 &\dots & 2 &-1 & 0 & 0 \\ 0 & 0 & 0 &\dots &-1 & 2 &-1 &-1 \\ 0 & 0 & 0 &\dots & 0 &-1 & 2 & 0 \\ 0 & 0 & 0 &\dots & 0 &-1 & 0 & 2 \\ \end{array} \right \| , $$ $$ E _{6} : \left \| \begin{array}{rrrrrr} 2 & 0 &-1 & 0 & 0 & 0 \\ 0 & 2 & 0 &-1 & 0 & 0 \\ -1 & 0 & 2 &-1 & 0 & 0 \\ 0 &-1 &-1 & 2 &-1 & 0 \\ 0 & 0 & 0 &-1 & 2 &-1 \\ 0 & 0 & 0 & 0 &-1 & 2 \\ \end{array} \right \| , $$ $$ E _{7} : \left \| \begin{array}{rrrrrrr} 2 & 0 &-1 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 &-1 & 0 & 0 & 0 \\ -1 & 0 & 2 &-1 & 0 & 0 & 0 \\ 0 &-1 &-1 & 2 &-1 & 0 & 0 \\ 0 & 0 & 0 &-1 & 2 &-1 & 0 \\ 0 & 0 & 0 & 0 &-1 & 2 &-1 \\ 0 & 0 & 0 & 0 & 0 &-1 & 2 \\ \end{array} \right \| , $$ $$ E _{8} : \left \| \begin{array}{rrrrrrrr} 2 & 0 &-1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 &-1 & 0 & 0 & 0 & 0 \\ -1 & 0 & 2 &-1 & 0 & 0 & 0 & 0 \\ 0 &-1 &-1 & 2 &-1 & 0 & 0 & 0 \\ 0 & 0 & 0 &-1 & 2 &-1 & 0 & 0 \\ 0 & 0 & 0 & 0 &-1 & 2 &-1 & 0 \\ 0 & 0 & 0 & 0 & 0 &-1 & 2 &-1 \\ 0 & 0 & 0 & 0 & 0 & 0 &-1 & 2 \\ \end{array} \right \| , $$ $$ F _{4} : \left \| \begin{array}{rrrr} 2 &-1 & 0 & 0 \\ -1 & 2 &-2 & 0 \\ 0 &-1 & 2 &-1 \\ 0 & 0 &-1 & 2 \\ \end{array} \right \| , G _{2} : \left \| \begin{array}{rr} 2 &-1 \\ -3 & 2 \\ \end{array} \right \| . $$ The classification of split semi-simple Lie algebras over an arbitrary field $ k $ of characteristic zero (a semi-simple Lie algebra $ \mathfrak g $ is said to be split if it has a Cartan subalgebra $ \mathfrak h \subset \mathfrak g $ such that all characteristic roots of the operators $ \mathop{\rm ad}\nolimits \ X $ , $ X \in \mathfrak h $ , lie in $ k $ ) goes in the same way as in the case of an algebraically closed field. Namely, to every irreducible reduced root system corresponds a unique split semi-simple Lie algebra. In particular, split semi-simple Lie algebras of types $ A $ – $ D $ have the form stated above, except that in the cases $ B $ and $ D $ one must consider non-singular symmetric bilinear forms with Witt index $ n $ .

The problem of classifying arbitrary semi-simple Lie algebras over $ k $ reduces to the following problem: To list, up to an isomorphism, all $ k $ -forms $ \mathfrak g _{0} \subset \mathfrak g $ , that is, all $ k $ -subalgebras $ \mathfrak g _{0} \subset \mathfrak g $ such that $ \mathfrak g = \mathfrak g _{0} \otimes _{k} K $ . Here $ K $ is an algebraically closed extension of $ k $ and $ \mathfrak g $ is a given semi-simple Lie algebra over $ K $ . The solution of this problem can also be obtained in terms of root systems (see Form of an algebraic group; Form of an (algebraic) structure). When $ \mathfrak g $ is a classical simple Lie algebra over $ k $ (other than $ D _{4} $ ), there is another method of classifying $ k $ -forms in $ \mathfrak g $ , based on an examination of simple associative algebras (see [3]).

When $ k = \mathbf R $ the classification of semi-simple Lie algebras goes as follows (see [6], [7]). Every simple non-Abelian Lie algebra over $ \mathbf R $ is either a simple Lie algebra over $ \mathbf C $ (regarded as an algebra over $ \mathbf R $ ), or the real form of a simple Lie algebra over $ \mathbf C $ . The classification of real forms $ \mathfrak g _{0} $ in a simple classical Lie algebra $ \mathfrak g $ over $ \mathbf C $ is as follows:

I) Type $ A _{n} $ : $ \mathfrak g = \mathfrak s \mathfrak l ( n + 1 ,\ \mathbf C ) $ , $ n \geq 1 $ . $ A _{I} $ : $ \mathfrak g _{0} = \mathfrak s \mathfrak l ( n + 1 ,\ \mathbf R ) $ . $ A _{II} $ : $ n + 1 = 2 m $ is even, $ \mathfrak g _{0} = \mathfrak s \mathfrak u ^ \ast ( 2 n ) $ , the subalgebra of elements of $ \mathfrak s \mathfrak l ( 2 m ,\ \mathbf C ) $ that preserve a certain quaternion structure. $ A _{III} $ : $ \mathfrak g _{0} = \mathfrak s \mathfrak u ( p ,\ n + 1 - p ) $ , the subalgebra of elements of $ \mathfrak s \mathfrak l ( n + 1 ,\ \mathbf C ) $ that are skew-symmetric with respect to a non-singular Hermitian form of positive index $ p $ , $ 0 \leq p \leq ( n + 1 ) / 2 . $

II) Type $ B _{n} $ : $ \mathfrak g = \mathfrak s \mathfrak o ( 2 n + 1 ,\ \mathbf C ) $ , $ n \geq 2 $ . $ B _{I} $ : $ \mathfrak g _{0} = \mathfrak s \mathfrak o ( p ,\ 2 n + 1 - p ) $ , the algebra of a linear transformations of the space $ \mathbf R ^{2n+1} $ that are skew-symmetric with respect to a non-singular symmetric bilinear form of positive index $ p $ , $ 0 \leq p \leq n $ .

III) Type $ C _{n} $ : $ \mathfrak g = \mathfrak s \mathfrak p (n,\ \mathbf C ) $ , $ n \geq 3 $ . $ C _{I} $ : $ \mathfrak g _{0} = \mathfrak s \mathfrak p ( n ,\ \mathbf R ) $ , the algebra of linear transformations of the space $ \mathbf R ^{2n} $ that are skew-symmetric with respect to a non-singular skew-symmetric bilinear form. $ C _{II} $ : $ \mathfrak g _{0} = \mathfrak s \mathfrak p ( p ,\ n - p ) $ , $ 0 \leq p \leq n / 2 $ , the subalgebra of $ \mathfrak s \mathfrak u ( 2 p ,\ 2 ( n - p ) ) $ consisting of transformations that preserve a certain quaternion structure.

IV) Type $ D _{n} $ : $ \mathfrak g = \mathfrak s \mathfrak o ( 2 n ,\ \mathbf C ) $ , $ n \geq 4 $ . $ D _{I} $ : $ \mathfrak g _{0} = \mathfrak s \mathfrak o ( p ,\ 2 n - p ) $ , the algebra of linear transformations of the space $ \mathbf R ^{2n} $ that are skew-symmetric with respect to a non-singular bilinear symmetric form of positive index $ p $ , $ 0 \leq p \leq n $ . $ D _{III} $ : $ \mathfrak g _{0} = \mathfrak s \mathfrak o ^ \ast ( 2 n ,\ \mathbf C ) $ , the subalgebra of $ \mathfrak s \mathfrak o (2n ,\ \mathbf C ) $ consisting of transformations that preserve a certain quaternion structure.

Semi-simple Lie algebras over the field $ \mathbf C $ were first considered in papers by W. Killing , who gave a classification of them, although in his proofs there were gaps, which were filled by E. Cartan [2]. In the papers of Killing and Cartan the roots of a Lie algebra appeared as the characteristic roots of the operator $ \mathop{\rm ad}\nolimits \ X $ . Cartan also gave a classification of real semi-simple Lie algebras by establishing a deep connection between these algebras and globally symmetric Riemannian spaces (cf. Globally symmetric Riemannian space).

References

[1a]	W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen I" Math. Ann. , 31 (1888) pp. 252–290 Zbl 20.0368.03
[1b]	W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen II" Math. Ann. , 33 (1889) pp. 1–48 Zbl 20.0368.03
[1c]	W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen III" Math. Ann. , 34 (1889) pp. 57–122 Zbl 21.0376.01
[1d]	W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen IV" Math. Ann. , 36 (1890) pp. 161–189 MR1510618
[2]	E. Cartan, "Sur la structure des groupes de transformations finis et continues" , Oeuvres complètes , 1 , Gauthier-Villars (1952) pp. 137–287
[3]	N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) MR0148716 MR0143793 Zbl 0121.27504 Zbl 0109.26201
[4]	J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803
[5]	R.G. Steinberg, "Lectures on Chevalley groups" , Yale Univ. Press (1967) MR0476871 MR0466335 Zbl 0307.22001 Zbl 1196.22001
[6]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) MR0514561 Zbl 0451.53038
[7]	S. Araki, "On root systems and an infinitesimal classification of irreducible symmetric spaces" Osaka J. Math. , 13 (1962) pp. 1–34 MR0153782 Zbl 0123.03002

Comments

The defining relations, mentioned above, $ ( \mathop{\rm ad}\nolimits \ X _ {\alpha _{i}} ) ^ {1 - n ( i , j )} ( X _ {\alpha _{j}} ) = 0 $ , are known as the Serre relations.

It is customary to encode the information contained in the Cartan matrices $ A _{n} $ – $ G _{2} $ by means of the so-called Dynkin diagrams.'

<tbody> </tbody> $ A _{n} $ ( $ n $ nodes) $ B _{n} $ ( $ n $ nodes, $ n \geq 2 $ ) $ C _{n} $ ( $ n $ nodes, $ n \geq 3 $ ) $ D _{n} $ ( $ n $ nodes, $ n \geq 4 $ ) $ E _{6} $ (6 nodes) $ E _{7} $ (7 nodes) $ E _{8} $ (8 nodes) $ F _{4} $ (4 nodes) $ G _{2} $ (2 nodes)

The rules for recovering the Cartan matrix from the corresponding Dynkin diagram (also called Dynkin graph occasionally) are as follows. Number the vertices, e.g.,

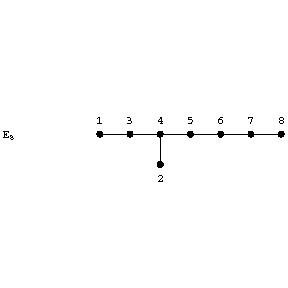
Figure: l058510a

On the diagonal of the Cartan matrix all elements are equal to 2. If nodes $ i $ and $ j $ are not directly linked, then the matrix entries $ a _{ji} = a _{ij} = 0 $ . If two nodes $ i $ , $ j $ are directly linked by a single edge, then $ a _{ij} = - 1 = a _{ji} $ . If two nodes $ i $ , $ j $ are directly linked by a double, respectively triple, edge and the arrow points from $ i $ to $ j $ , then $ a _{ij} = - 2 $ , $ a _{ji} = - 1 $ , respectively $ a _{ij} = - 3 $ , $ a _{ji} = - 1 $ .

References

[a1]	I.B. Frenkel, V.G. Kac, "Basic representations of affine Lie algebras and dual resonance models" Invent. Math. , 62 (1980) pp. 23–66 MR0595581 Zbl 0493.17010
[a2]	N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) MR0682756 Zbl 0319.17002
[a3]	J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) MR0215886 Zbl 0144.02105
[a4]	J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 MR0323842 Zbl 0254.17004