Difference between revisions of "Sasakian manifold"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
m (fixing spaces) |
||
| Line 12: | Line 12: | ||
Let $ M $ | Let $ M $ | ||
| − | be a $ ( 2m + 1 ) $- | + | be a $ ( 2m + 1 ) $-dimensional [[Differentiable manifold|differentiable manifold]] of class $ C ^ \infty $ |
| − | dimensional [[Differentiable manifold|differentiable manifold]] of class $ C ^ \infty $ | ||
and let $ \phi, \xi, \eta $ | and let $ \phi, \xi, \eta $ | ||
| − | be a tensor field of type $ ( 1,1 ) $( | + | be a tensor field of type $ ( 1,1 ) $ (cf. also [[Tensor on a vector space|Tensor on a vector space]]), a [[Vector field|vector field]] and a $ 1 $-form on $ M $ (cf. [[Differential form|Differential form]]), respectively, such that |
| − | cf. also [[Tensor on a vector space|Tensor on a vector space]]), a [[Vector field|vector field]] and a $ 1 $- | ||
| − | form on $ M $( | ||
| − | cf. [[Differential form|Differential form]]), respectively, such that | ||
$$ | $$ | ||
| Line 56: | Line 52: | ||
is said to be an almost contact metric structure and $ M $ | is said to be an almost contact metric structure and $ M $ | ||
an almost contact metric manifold. On $ M $ | an almost contact metric manifold. On $ M $ | ||
| − | one defines the fundamental $ 2 $- | + | one defines the fundamental $ 2 $-form $ \Phi $ |
| − | form $ \Phi $ | ||
by | by | ||
| Line 105: | Line 100: | ||
A plane section $ \pi $ | A plane section $ \pi $ | ||
in $ T _ {x} M $ | in $ T _ {x} M $ | ||
| − | is called a $ \phi $- | + | is called a $ \phi $-section if there exists a unit vector $ X $ |
| − | section if there exists a unit vector $ X $ | ||
in $ T _ {x} M $ | in $ T _ {x} M $ | ||
orthogonal to $ \xi $ | orthogonal to $ \xi $ | ||
such that $ \{ X, \phi X \} $ | such that $ \{ X, \phi X \} $ | ||
is an orthonormal basis of $ \pi $. | is an orthonormal basis of $ \pi $. | ||
| − | The $ \phi $- | + | The $ \phi $-sectional curvature of $ M $ |
| − | sectional curvature of $ M $ | + | with respect to a $ \phi $-section $ \pi $ |
| − | with respect to a $ \phi $- | ||
| − | section $ \pi $ | ||
is defined by $ H ( \pi ) = g ( R ( X, \phi X ) \phi X,X ) $, | is defined by $ H ( \pi ) = g ( R ( X, \phi X ) \phi X,X ) $, | ||
where $ R $ | where $ R $ | ||
is the curvature tensor field of $ \nabla $. | is the curvature tensor field of $ \nabla $. | ||
| − | When the $ \phi $- | + | When the $ \phi $-sectional curvature does not depend on both the point $ x \in M $ |
| − | sectional curvature does not depend on both the point $ x \in M $ | + | and the $ \phi $-section $ \pi $, |
| − | and the $ \phi $- | ||
| − | section $ \pi $, | ||
one says that $ M $ | one says that $ M $ | ||
| − | has constant $ \phi $- | + | has constant $ \phi $-sectional curvature and calls it a Sasakian space form. |
| − | sectional curvature and calls it a Sasakian space form. | ||
General references for Sasakian manifolds are [[#References|[a2]]], [[#References|[a3]]], [[#References|[a6]]]. | General references for Sasakian manifolds are [[#References|[a2]]], [[#References|[a3]]], [[#References|[a6]]]. | ||
| Line 133: | Line 122: | ||
First, let $ N $ | First, let $ N $ | ||
| − | be a $ ( 2n + 1 ) $- | + | be a $ ( 2n + 1 ) $-dimensional submanifold of $ M $ |
| − | dimensional submanifold of $ M $ | ||
such that $ \xi $ | such that $ \xi $ | ||
is tangent to $ N $ | is tangent to $ N $ | ||
| Line 145: | Line 133: | ||
inherits the properties of the ambient Sasakian manifold $ M $. | inherits the properties of the ambient Sasakian manifold $ M $. | ||
| − | Next, an $ n $- | + | Next, an $ n $-dimensional submanifold $ N $ |
| − | dimensional submanifold $ N $ | ||
of $ M $ | of $ M $ | ||
is an anti-invariant submanifold if $ \phi ( T _ {x} N ) \subset T _ {x} N ^ \perp $ | is an anti-invariant submanifold if $ \phi ( T _ {x} N ) \subset T _ {x} N ^ \perp $ | ||
| Line 155: | Line 142: | ||
The most important results on anti-invariant submanifolds have been collected in [[#References|[a5]]]. | The most important results on anti-invariant submanifolds have been collected in [[#References|[a5]]]. | ||
| − | Finally, an $ n $- | + | Finally, an $ n $-dimensional submanifold $ N $ |
| − | dimensional submanifold $ N $ | ||
of $ M $ | of $ M $ | ||
is said to be a semi-invariant submanifold (a contact CR-submanifold; cf. also [[CR-submanifold|CR-submanifold]]) if $ \xi $ | is said to be a semi-invariant submanifold (a contact CR-submanifold; cf. also [[CR-submanifold|CR-submanifold]]) if $ \xi $ | ||
Latest revision as of 01:08, 8 May 2022
Let $ M $
be a $ ( 2m + 1 ) $-dimensional differentiable manifold of class $ C ^ \infty $
and let $ \phi, \xi, \eta $
be a tensor field of type $ ( 1,1 ) $ (cf. also Tensor on a vector space), a vector field and a $ 1 $-form on $ M $ (cf. Differential form), respectively, such that
$$ \phi ^ {2} = - I + \eta \otimes \xi, \quad \eta ( \xi ) = 1, $$
where $ I $ is the identity on the tangent bundle $ TM $ of $ M $. Then $ ( \phi, \xi, \eta ) $ is said to be an almost contact structure on $ M $, and $ M $ is called an almost contact manifold. If follows that
$$ \eta \circ \phi = 0, \quad \phi ( \xi ) = 0, $$
and therefore $ \phi $ has the constant rank $ 2m $ on $ M $. Moreover, there exists a Riemannian metric $ g $ on $ M $ such that
$$ g ( \phi x, \phi Y ) = g ( X,Y ) - \eta ( X ) \eta ( Y ) , $$
$$ \eta ( X ) = g ( X, \xi ) , $$
for any vector fields $ X $, $ Y $ on $ M $[a2]. Then $ ( \phi, \xi, \eta,g ) $ is said to be an almost contact metric structure and $ M $ an almost contact metric manifold. On $ M $ one defines the fundamental $ 2 $-form $ \Phi $ by
$$ \Phi ( X,Y ) = g ( X, \phi Y ) . $$
Then $ ( \phi, \xi, \eta,g ) $ is said to be a contact metric structure on $ M $ if $ \Phi = d \eta $.
The Nijenhuis tensor field of $ \phi $ is the tensor field $ [ \phi, \phi] $ of type $ ( 1,2 ) $ given by
$$ [ \phi, \phi ] ( X,Y ) = \phi ^ {2} [ X,Y ] - [ \phi X, \phi Y ] + $$
$$ - \phi [ \phi X,Y ] - \phi [ X, \phi Y ] . $$
The almost contact structure $ ( \phi, \xi, \eta ) $ is said to be normal if
$$ [ \phi, \phi ] + 2d \eta \otimes \xi = 0. $$
A manifold $ M $ endowed with a normal contact metric structure is called a Sasakian manifold. To study Sasakian manifolds one often uses the following characterization (cf. [a4]): An almost contact metric manifold $ M $ is Sasakian if and only if
$$ ( \nabla _ {X} \phi ) Y = g ( X,Y ) \xi - \eta ( Y ) X, $$
for any vector fields $ X $, $ Y $ on $ M $, where $ \nabla $ is the Levi-Civita connection on $ M $ with respect to $ g $.
A plane section $ \pi $ in $ T _ {x} M $ is called a $ \phi $-section if there exists a unit vector $ X $ in $ T _ {x} M $ orthogonal to $ \xi $ such that $ \{ X, \phi X \} $ is an orthonormal basis of $ \pi $. The $ \phi $-sectional curvature of $ M $ with respect to a $ \phi $-section $ \pi $ is defined by $ H ( \pi ) = g ( R ( X, \phi X ) \phi X,X ) $, where $ R $ is the curvature tensor field of $ \nabla $. When the $ \phi $-sectional curvature does not depend on both the point $ x \in M $ and the $ \phi $-section $ \pi $, one says that $ M $ has constant $ \phi $-sectional curvature and calls it a Sasakian space form.
General references for Sasakian manifolds are [a2], [a3], [a6].
Submanifolds of Sasakian manifolds.
Three classes of submanifolds of a Sasakian manifold $ M $ have been studied intensively.
First, let $ N $ be a $ ( 2n + 1 ) $-dimensional submanifold of $ M $ such that $ \xi $ is tangent to $ N $ and $ \phi ( T _ {x} N ) \subset T _ {x} N $, for all $ x \in N $. Then $ N $ is said to be an invariant submanifold of $ M $. It follows that $ N $ is a Sasakian manifold too, and, in general, $ N $ inherits the properties of the ambient Sasakian manifold $ M $.
Next, an $ n $-dimensional submanifold $ N $ of $ M $ is an anti-invariant submanifold if $ \phi ( T _ {x} N ) \subset T _ {x} N ^ \perp $ for all $ x \in N $, where $ T _ {x} N ^ \perp $ is the normal space of $ N $ at $ x $. The most important results on anti-invariant submanifolds have been collected in [a5].
Finally, an $ n $-dimensional submanifold $ N $ of $ M $ is said to be a semi-invariant submanifold (a contact CR-submanifold; cf. also CR-submanifold) if $ \xi $ is tangent to $ N $ and there exist two distributions $ D $ and $ D ^ \perp $ on $ N $ such that $ TN $ has the orthogonal decomposition $ TN = D \oplus D ^ \perp \oplus \{ \xi \} $, with $ \phi ( D _ {x} ) = D _ {x} $ and $ \phi ( D _ {x} ^ \perp ) \subset T _ {x} N ^ \perp $ for all $ x \in N $, where $ \{ \xi \} $ denotes the distribution spanned by $ \xi $ on $ N $. For the geometry of semi-invariant submanifolds, see [a1].
References
| [a1] | A. Bejancu, "Geometry of 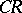 submanifolds" , Reidel (1986) submanifolds" , Reidel (1986) |
| [a2] | D.E. Blair, "Contact manifolds in Riemannian geometry" , Lecture Notes in Mathematics , 509 , Springer (1976) |
| [a3] | S. Sasaki, "Almost contact manifolds" , Lecture Notes , 1–3 , Math. Inst. Tôhoku Univ. (1965–1968) |
| [a4] | S. Sasaki, Y. Hatakeyama, "On differentiable manifolds with contact metric strctures" J. Math. Soc. Japan , 14 (1962) pp. 249–271 |
| [a5] | K. Yano, M. Kon, "Anti-invariant submanifolds" , M. Dekker (1976) |
| [a6] | K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984) |
Sasakian manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sasakian_manifold&oldid=52320