Difference between revisions of "Representation of the classical groups"
m (fixing superscripts) |
m (fixing mathop) |
||
| Line 14: | Line 14: | ||
Linear representations (cf. [[Linear representation|Linear representation]]) of the groups $ \mathop{\rm GL} ( V) $, | Linear representations (cf. [[Linear representation|Linear representation]]) of the groups $ \mathop{\rm GL} ( V) $, | ||
| − | $ \ | + | $ \textrm{SL} ( V) $, |
| − | $ \textrm{ O } ( V, f ) $, | + | $ \textrm{O} ( V, f ) $, |
| − | $ \ | + | $ \textrm{SO} ( V, f ) $, |
| − | $ \ | + | $ \textrm{Sp} ( V, f ) $, |
where $ V $ | where $ V $ | ||
is an $ n $-dimensional vector space over a field $ k $ | is an $ n $-dimensional vector space over a field $ k $ | ||
| Line 28: | Line 28: | ||
In the case $ k = \mathbf C $ | In the case $ k = \mathbf C $ | ||
| − | the groups above are complex Lie groups. For all groups, except $ | + | the groups above are complex Lie groups. For all groups, except $ \textrm{GL} ( V) $, |
| − | all (differentiable) linear representations are polynomial; every linear representation of $ \ | + | all (differentiable) linear representations are polynomial; every linear representation of $ \textrm{ GL} ( V) $ |
| − | has the form $ g \mapsto ( \ | + | has the form $ g \mapsto ( \det g) ^ {k} R ( g) $, |
where $ k \in \mathbf Z $ | where $ k \in \mathbf Z $ | ||
and $ R $ | and $ R $ | ||
| − | is a polynomial linear representation. The classical compact Lie groups $ \textrm{ U } _ {n} $, | + | is a polynomial linear representation. The classical compact Lie groups $ \textrm{U} _ {n} $, |
| − | $ \ | + | $ \textrm{SU} _ {n} $, |
| − | $ \textrm{ O } _ {n} $, | + | $ \textrm{O} _ {n} $, |
| − | $ \ | + | $ \textrm{SO} _ {n} $, |
| − | and $ | + | and $ \textrm{Sp} _ {n} $ |
| − | have the same complex linear representations and the same invariant subspaces in tensor spaces as their complex envelopes $ \textrm{ U } _ {n} ( \mathbf C ) $, | + | have the same complex linear representations and the same invariant subspaces in tensor spaces as their complex envelopes $ \textrm{U} _ {n} ( \mathbf C ) $, |
| − | $ \ | + | $ \textrm{SL} _ {n} ( \mathbf C ) $, |
| − | $ \textrm{ O } _ {n} ( \mathbf C ) $, | + | $ \textrm{O} _ {n} ( \mathbf C ) $, |
| − | $ \ | + | $ \textrm{SO} _ {n} ( \mathbf C ) $, |
| − | and $ \ | + | and $ \textrm{Sp} _ {n} ( \mathbf C ) $. |
Therefore, results of the theory of linear representations obtained for the classical complex Lie groups can be carried over to the corresponding compact groups and vice versa (Weyl's "unitary trick" ). In particular, using integration on a compact group one can prove that linear representations of the classical complex Lie groups are completely reducible. | Therefore, results of the theory of linear representations obtained for the classical complex Lie groups can be carried over to the corresponding compact groups and vice versa (Weyl's "unitary trick" ). In particular, using integration on a compact group one can prove that linear representations of the classical complex Lie groups are completely reducible. | ||
| − | The natural linear representation of $ | + | The natural linear representation of $ \textrm{ GL} ( V) $ |
in $ T ^ {m} ( V) $ | in $ T ^ {m} ( V) $ | ||
is given by the formula | is given by the formula | ||
| Line 52: | Line 52: | ||
g ( v _ {1} \otimes \dots \otimes v _ {m} ) = \ | g ( v _ {1} \otimes \dots \otimes v _ {m} ) = \ | ||
gv _ {1} \otimes \dots \otimes gv _ {m} ,\ \ | gv _ {1} \otimes \dots \otimes gv _ {m} ,\ \ | ||
| − | g \in \ | + | g \in \textrm{ GL} ( V),\ \ |
v _ {i} \in V. | v _ {i} \in V. | ||
$$ | $$ | ||
| Line 67: | Line 67: | ||
$$ | $$ | ||
| − | The operators of these two representations commute, so that a linear representation of $ | + | The operators of these two representations commute, so that a linear representation of $ \textrm{GL} ( V) \times S _ {m} $ |
is defined in $ T ^ {m} ( V) $. | is defined in $ T ^ {m} ( V) $. | ||
If $ \mathop{\rm char} k = 0 $, | If $ \mathop{\rm char} k = 0 $, | ||
the space $ T ^ {m} ( V) $ | the space $ T ^ {m} ( V) $ | ||
| − | can be decomposed into a direct sum of minimal $ ( | + | can be decomposed into a direct sum of minimal $ ( \textrm{GL} ( V) \times S _ {m} ) $-invariant subspaces: |
$$ | $$ | ||
| Line 86: | Line 86: | ||
corresponding to $ \lambda $ (cf. [[Representation of the symmetric groups|Representation of the symmetric groups]]) and $ V _ \lambda $ | corresponding to $ \lambda $ (cf. [[Representation of the symmetric groups|Representation of the symmetric groups]]) and $ V _ \lambda $ | ||
is the space of an absolutely-irreducible representation $ R _ \lambda $ | is the space of an absolutely-irreducible representation $ R _ \lambda $ | ||
| − | of $ | + | of $ \textrm{GL} ( V) $. |
A partition $ \lambda $ | A partition $ \lambda $ | ||
can be conveniently represented by a tuple $ ( \lambda _ {1} \dots \lambda _ {n} ) $ | can be conveniently represented by a tuple $ ( \lambda _ {1} \dots \lambda _ {n} ) $ | ||
| Line 93: | Line 93: | ||
The subspace $ V _ \lambda \otimes U _ \lambda \subset T ^ {m} ( V) $ | The subspace $ V _ \lambda \otimes U _ \lambda \subset T ^ {m} ( V) $ | ||
| − | splits in a sum of minimal $ | + | splits in a sum of minimal $ \textrm{GL} ( V) $-invariant subspaces, in each of which a representation $ R _ \lambda $ |
can be realized. These subspaces can be explicitly obtained by using Young symmetrizers (cf. [[Young symmetrizer|Young symmetrizer]]) connected with $ \lambda $. | can be realized. These subspaces can be explicitly obtained by using Young symmetrizers (cf. [[Young symmetrizer|Young symmetrizer]]) connected with $ \lambda $. | ||
E.g. for $ \lambda = ( m, 0 \dots 0) $ (respectively, $ \lambda = ( 1 \dots 1, 0 \dots 0) $ | E.g. for $ \lambda = ( m, 0 \dots 0) $ (respectively, $ \lambda = ( 1 \dots 1, 0 \dots 0) $ | ||
for $ m \leq n $) | for $ m \leq n $) | ||
| − | one has $ | + | one has $ \dim U _ \lambda = 1 $ |
and $ V _ \lambda \otimes U _ \lambda $ | and $ V _ \lambda \otimes U _ \lambda $ | ||
| − | is the minimal $ | + | is the minimal $ \textrm{GL} ( V) $-invariant subspace consisting of all symmetric (respectively, skew-symmetric) tensors. |
The representation $ R _ \lambda $ | The representation $ R _ \lambda $ | ||
| − | is characterized by the following properties. Let $ B \subset | + | is characterized by the following properties. Let $ B \subset \textrm{GL} ( V) $ |
be the subgroup of all linear operators that, in some basis $ \{ e _ {1} \dots e _ {n} \} $ | be the subgroup of all linear operators that, in some basis $ \{ e _ {1} \dots e _ {n} \} $ | ||
of $ V $, | of $ V $, | ||
| Line 120: | Line 120: | ||
$$ | $$ | ||
| − | \ | + | \tr R _ \lambda ( g) = \ |
\frac{W _ \lambda ( z _ {1} \dots z _ {n} ) }{W _ {0} ( z _ {1} \dots z _ {n} ) } | \frac{W _ \lambda ( z _ {1} \dots z _ {n} ) }{W _ {0} ( z _ {1} \dots z _ {n} ) } | ||
| Line 134: | Line 134: | ||
$$ | $$ | ||
| − | + | \dim R _ \lambda = \ | |
\prod _ {i < j } | \prod _ {i < j } | ||
| Line 144: | Line 144: | ||
The restriction of $ R _ \lambda $ | The restriction of $ R _ \lambda $ | ||
| − | to the [[Unimodular group|unimodular group]] $ | + | to the [[Unimodular group|unimodular group]] $ \textrm{SL} ( V) $ |
| − | is irreducible. The restrictions to $ | + | is irreducible. The restrictions to $ \textrm{SL} ( V) $ |
of two representations $ R _ \lambda $ | of two representations $ R _ \lambda $ | ||
and $ R _ \mu $ | and $ R _ \mu $ | ||
| Line 151: | Line 151: | ||
is independent of $ i $). | is independent of $ i $). | ||
The restriction of a representation $ R _ \lambda $ | The restriction of a representation $ R _ \lambda $ | ||
| − | of $ | + | of $ \textrm{GL} _ {n} ( k) $ |
| − | to the subgroup $ \ | + | to the subgroup $ \textrm{GL} _ {n - 1 } ( k) $ |
can be found by the rule: | can be found by the rule: | ||
$$ | $$ | ||
| − | R _ \lambda \mid _ { \ | + | R _ \lambda \mid _ { \textrm{GL} _ {n - 1 } ( k) } = \ |
\sum _ \mu R _ \mu , | \sum _ \mu R _ \mu , | ||
$$ | $$ | ||
| Line 224: | Line 224: | ||
one obtains the Young tableau of a partition $ \overline \lambda $ | one obtains the Young tableau of a partition $ \overline \lambda $ | ||
which also satisfies this condition. The corresponding representations of $ \textrm{ O } ( V, f ) $ | which also satisfies this condition. The corresponding representations of $ \textrm{ O } ( V, f ) $ | ||
| − | are related by $ R _ {\overline \lambda } ^ {0} ( g) = ( | + | are related by $ R _ {\overline \lambda } ^ {0} ( g) = ( \det g) R _ \lambda ^ {0} ( g) $ (in particular, they have equal dimension). |
The restriction of $ R _ \lambda ^ {0} $ | The restriction of $ R _ \lambda ^ {0} $ | ||
| − | to the subgroup $ | + | to the subgroup $ \textrm{SO} ( V, f ) $ |
is absolutely irreducible, except in the case $ n $ | is absolutely irreducible, except in the case $ n $ | ||
even and $ \lambda = \overline \lambda $ (i.e. the number of terms of $ \lambda $ | even and $ \lambda = \overline \lambda $ (i.e. the number of terms of $ \lambda $ | ||
| Line 242: | Line 242: | ||
$$ | $$ | ||
| − | + | \dim R _ \lambda ^ {0} = \ | |
\prod _ {i = 1 } ^ { [ n/2]} | \prod _ {i = 1 } ^ { [ n/2]} | ||
| Line 262: | Line 262: | ||
$$ | $$ | ||
| − | \ | + | \dim R _ \lambda ^ {0} = \ |
\prod _ {\begin{array}{c} | \prod _ {\begin{array}{c} | ||
i, j = 1 \\ | i, j = 1 \\ | ||
| Line 275: | Line 275: | ||
For $ \lambda = \overline \lambda $ | For $ \lambda = \overline \lambda $ | ||
the latter formula gives half the dimension of $ R _ \lambda ^ {0} $, | the latter formula gives half the dimension of $ R _ \lambda ^ {0} $, | ||
| − | i.e. the dimension of each of the absolutely-irreducible representations of $ | + | i.e. the dimension of each of the absolutely-irreducible representations of $ \textrm{SO} ( V, f ) $ |
corresponding to it. | corresponding to it. | ||
The decomposition of $ T ^ {m} ( V) $ | The decomposition of $ T ^ {m} ( V) $ | ||
| − | with respect to the [[Symplectic group|symplectic group]] $ | + | with respect to the [[Symplectic group|symplectic group]] $ \textrm{Sp} ( V, f ) $ |
is analogous to the decomposition with respect to the orthogonal group, with the difference that $ V _ \lambda ^ {0} \neq 0 $ | is analogous to the decomposition with respect to the orthogonal group, with the difference that $ V _ \lambda ^ {0} \neq 0 $ | ||
if and only if $ \lambda _ {1} ^ \prime \leq n/2 $. | if and only if $ \lambda _ {1} ^ \prime \leq n/2 $. | ||
| Line 286: | Line 286: | ||
$$ | $$ | ||
| − | + | \dim R _ \lambda ^ {0} = \ | |
\prod _ {i = 1 } ^ { n/2 } | \prod _ {i = 1 } ^ { n/2 } | ||
| Line 307: | Line 307: | ||
====Comments==== | ====Comments==== | ||
| − | This article describes the classical theory. The contemporary period in this old field of algebra began with [[#References|[a1]]]. It can be described by two words: "characteristic-free representation theory" . A different approach to the polynomial representations of $ | + | This article describes the classical theory. The contemporary period in this old field of algebra began with [[#References|[a1]]]. It can be described by two words: "characteristic-free representation theory" . A different approach to the polynomial representations of $ \textrm{GL} ( V) $ |
| − | and $ | + | and $ \textrm{SL} ( V) $ |
was undertaken in [[#References|[a2]]]. Further, both classical and characteristic free theories can be found in [[#References|[a3]]]. | was undertaken in [[#References|[a2]]]. Further, both classical and characteristic free theories can be found in [[#References|[a3]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.W. Carter, G. Lustig, "On the modular representations of the general linear and symmetric groups" ''Math. Z.'' , '''136''' (1974) pp. 193–242 {{MR|0369503}} {{MR|0354887}} {{ZBL|0301.20005}} {{ZBL|0298.20009}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.A. Green, "Polynomial representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081460/r081460174.png" />" , ''Lect. notes in math.'' , '''830''' , Springer (1980) {{MR|0606556}} {{ZBL|0451.20037}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G. James, A. Kerber, "The representation theory of the symmetric group" , Addison-Wesley (1981) {{MR|0644144}} {{ZBL|0491.20010}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W. Feit, "The representation theory of finite groups" , North-Holland (1982) {{MR|0661045}} {{ZBL|0493.20007}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.W. Carter, G. Lustig, "On the modular representations of the general linear and symmetric groups" ''Math. Z.'' , '''136''' (1974) pp. 193–242 {{MR|0369503}} {{MR|0354887}} {{ZBL|0301.20005}} {{ZBL|0298.20009}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.A. Green, "Polynomial representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081460/r081460174.png" />" , ''Lect. notes in math.'' , '''830''' , Springer (1980) {{MR|0606556}} {{ZBL|0451.20037}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G. James, A. Kerber, "The representation theory of the symmetric group" , Addison-Wesley (1981) {{MR|0644144}} {{ZBL|0491.20010}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W. Feit, "The representation theory of finite groups" , North-Holland (1982) {{MR|0661045}} {{ZBL|0493.20007}} </TD></TR></table> | ||
Revision as of 07:53, 5 May 2022
in tensors
Linear representations (cf. Linear representation) of the groups $ \mathop{\rm GL} ( V) $, $ \textrm{SL} ( V) $, $ \textrm{O} ( V, f ) $, $ \textrm{SO} ( V, f ) $, $ \textrm{Sp} ( V, f ) $, where $ V $ is an $ n $-dimensional vector space over a field $ k $ and $ f $ is a non-degenerate symmetric or alternating bilinear form on $ V $, in invariant subspaces of tensor powers $ T ^ {m} ( V) $ of $ V $. If the characteristic of $ k $ is zero, then all irreducible polynomial linear representations of these groups can be realized by means of tensors.
In the case $ k = \mathbf C $ the groups above are complex Lie groups. For all groups, except $ \textrm{GL} ( V) $, all (differentiable) linear representations are polynomial; every linear representation of $ \textrm{ GL} ( V) $ has the form $ g \mapsto ( \det g) ^ {k} R ( g) $, where $ k \in \mathbf Z $ and $ R $ is a polynomial linear representation. The classical compact Lie groups $ \textrm{U} _ {n} $, $ \textrm{SU} _ {n} $, $ \textrm{O} _ {n} $, $ \textrm{SO} _ {n} $, and $ \textrm{Sp} _ {n} $ have the same complex linear representations and the same invariant subspaces in tensor spaces as their complex envelopes $ \textrm{U} _ {n} ( \mathbf C ) $, $ \textrm{SL} _ {n} ( \mathbf C ) $, $ \textrm{O} _ {n} ( \mathbf C ) $, $ \textrm{SO} _ {n} ( \mathbf C ) $, and $ \textrm{Sp} _ {n} ( \mathbf C ) $. Therefore, results of the theory of linear representations obtained for the classical complex Lie groups can be carried over to the corresponding compact groups and vice versa (Weyl's "unitary trick" ). In particular, using integration on a compact group one can prove that linear representations of the classical complex Lie groups are completely reducible.
The natural linear representation of $ \textrm{ GL} ( V) $ in $ T ^ {m} ( V) $ is given by the formula
$$ g ( v _ {1} \otimes \dots \otimes v _ {m} ) = \ gv _ {1} \otimes \dots \otimes gv _ {m} ,\ \ g \in \textrm{ GL} ( V),\ \ v _ {i} \in V. $$
In the same space a linear representation of the symmetric group $ S _ {m} $ is defined by
$$ \sigma ( v _ {1} \otimes \dots \otimes v _ {m} ) = \ v _ {\sigma ^ {- 1 }( 1) } \otimes \dots \otimes v _ {\sigma ^ {- 1 }( m) } ,\ \ \sigma \in S _ {m} ,\ \ v _ {i} \in V. $$
The operators of these two representations commute, so that a linear representation of $ \textrm{GL} ( V) \times S _ {m} $ is defined in $ T ^ {m} ( V) $. If $ \mathop{\rm char} k = 0 $, the space $ T ^ {m} ( V) $ can be decomposed into a direct sum of minimal $ ( \textrm{GL} ( V) \times S _ {m} ) $-invariant subspaces:
$$ T ^ {m} ( V) = \ \sum _ \lambda V _ \lambda \otimes U _ \lambda . $$
The summation is over all partitions $ \lambda $ of $ m $ containing at most $ n $ summands, $ U _ \lambda $ is the space of the absolutely-irreducible representation $ T _ \lambda $ of $ S _ {m} $ corresponding to $ \lambda $ (cf. Representation of the symmetric groups) and $ V _ \lambda $ is the space of an absolutely-irreducible representation $ R _ \lambda $ of $ \textrm{GL} ( V) $. A partition $ \lambda $ can be conveniently represented by a tuple $ ( \lambda _ {1} \dots \lambda _ {n} ) $ of non-negative integers satisfying $ \lambda _ {1} \geq \dots \geq \lambda _ {n} $ and $ \sum _ {i} \lambda _ {i} = m $.
The subspace $ V _ \lambda \otimes U _ \lambda \subset T ^ {m} ( V) $ splits in a sum of minimal $ \textrm{GL} ( V) $-invariant subspaces, in each of which a representation $ R _ \lambda $ can be realized. These subspaces can be explicitly obtained by using Young symmetrizers (cf. Young symmetrizer) connected with $ \lambda $. E.g. for $ \lambda = ( m, 0 \dots 0) $ (respectively, $ \lambda = ( 1 \dots 1, 0 \dots 0) $ for $ m \leq n $) one has $ \dim U _ \lambda = 1 $ and $ V _ \lambda \otimes U _ \lambda $ is the minimal $ \textrm{GL} ( V) $-invariant subspace consisting of all symmetric (respectively, skew-symmetric) tensors.
The representation $ R _ \lambda $ is characterized by the following properties. Let $ B \subset \textrm{GL} ( V) $ be the subgroup of all linear operators that, in some basis $ \{ e _ {1} \dots e _ {n} \} $ of $ V $, can be written as upper-triangular matrices. Then the operators $ R _ \lambda ( b) $, $ b \in B $, have a unique (up to a numerical factor) common eigenvector $ v _ \lambda $, which is called the highest weight vector of $ R _ \lambda $. The corresponding eigenvalue (the highest weight of $ R _ \lambda $) is equal to $ b _ {11} ^ {\lambda _ {1} } \dots b _ {nn} ^ {\lambda _ {n} } $, where $ b _ {ii} $ is the $ i $-th diagonal element of the matrix of $ b $ in the basis $ \{ e _ {1} \dots e _ {n} \} $. Representations $ R _ \lambda $ corresponding to distinct partitions $ \lambda $ are inequivalent. The character of $ R _ \lambda $ can be found from Weyl's formula
$$ \tr R _ \lambda ( g) = \ \frac{W _ \lambda ( z _ {1} \dots z _ {n} ) }{W _ {0} ( z _ {1} \dots z _ {n} ) } , $$
where $ z _ {1} \dots z _ {n} $ are the roots of the characteristic polynomial of the operator $ g $, $ W _ \lambda $ is the generalized Vandermonde determinant corresponding to $ \lambda $ (cf. Frobenius formula) and $ W _ {0} $ is the ordinary Vandermonde determinant. The dimension of $ R _ \lambda $ is equal to
$$ \dim R _ \lambda = \ \prod _ {i < j } \frac{l _ {i} - l _ {j} }{j - i } , $$
where $ l _ {i} = \lambda _ {i} + n - i $.
The restriction of $ R _ \lambda $ to the unimodular group $ \textrm{SL} ( V) $ is irreducible. The restrictions to $ \textrm{SL} ( V) $ of two representations $ R _ \lambda $ and $ R _ \mu $ are equivalent if and only if $ \mu _ {i} = \lambda _ {i} + s $ (where $ s $ is independent of $ i $). The restriction of a representation $ R _ \lambda $ of $ \textrm{GL} _ {n} ( k) $ to the subgroup $ \textrm{GL} _ {n - 1 } ( k) $ can be found by the rule:
$$ R _ \lambda \mid _ { \textrm{GL} _ {n - 1 } ( k) } = \ \sum _ \mu R _ \mu , $$
where $ \mu $ runs through all tuples $ ( \mu _ {1} \dots \mu _ {n - 1 } ) $ satisfying
$$ \lambda _ {1} \geq \mu _ {1} \geq \ \lambda _ {2} \geq \mu _ {2} \geq \dots \geq \lambda _ {n} . $$
For every Young diagram $ d $, corresponding to a partition $ \lambda $, the tensor $ v _ \lambda \otimes u _ {d} ^ \prime \in T ^ {m} ( V) $ (for notations see Representation of the symmetric groups) is the result of alternating the tensor $ e _ {i _ {1} } \otimes \dots \otimes e _ {i _ {m} } $ over the columns of $ d $, where $ i _ {k} $ is the number of the row of $ d $ in which the number $ k $ is located. The tensors thus constructed with respect to all standard diagrams $ d $ form a basis of the minimal $ S _ {m} $-invariant subspace of $ v _ \lambda \otimes U _ \lambda $ in which the representation $ T _ \lambda $ of $ S _ {m} $ is realized.
A linear representation of the orthogonal group $ \textrm{ O } ( V, f ) $ in $ T ^ {m} ( V) $ has the following structure. There is a decomposition into a direct sum of two $ ( \textrm{ O } ( V, f ) \times S _ {m} ) $-invariant subspaces:
$$ T ^ {m} ( V) = T _ {0} ^ {m} ( V) \oplus T _ {1} ^ {m} ( V) , $$
where $ T _ {0} ^ {m} ( V) $ consists of traceless tensors, i.e. tensors whose convolution with $ f $ over any two indices vanishes, and
$$ T _ {1} ^ {m} ( V) = \ \sum _ {\sigma \in S _ {m} } \sigma ( T ^ {m - 2 } ( V) \otimes f ^ { - 1 } ). $$
The space $ T _ {0} ^ {m} ( V) $, in turn, decomposes into a direct sum of $ ( \textrm{ O } ( V, f ) \times S _ {m} ) $-invariant subspaces:
$$ T _ {0} ^ {m} ( V) = \ \sum _ \lambda V _ \lambda ^ {0} \otimes U _ \lambda , $$
where $ V _ \lambda ^ {0} \subset V _ \lambda $. Moreover, $ V _ \lambda ^ {0} \neq 0 $ if and only if the sum $ \lambda _ {1} ^ \prime + \lambda _ {2} ^ \prime $ of the heights of the first two columns of the Young tableau corresponding to $ \lambda $ does not exceed $ n $, and in this case $ V _ \lambda ^ {0} $ is the space of an absolutely-irreducible representation $ R _ \lambda ^ {0} $ of $ \textrm{ O } ( V, f ) $. Representations $ R _ \lambda ^ {0} $ corresponding to distinct partitions $ \lambda $ are inequivalent. If $ \lambda $ satisfies the condition $ \lambda _ {1} ^ \prime + \lambda _ {2} ^ \prime \leq n $, then after replacing the first column of its Young tableau by a column of height $ n - \lambda _ {1} ^ \prime $ one obtains the Young tableau of a partition $ \overline \lambda $ which also satisfies this condition. The corresponding representations of $ \textrm{ O } ( V, f ) $ are related by $ R _ {\overline \lambda } ^ {0} ( g) = ( \det g) R _ \lambda ^ {0} ( g) $ (in particular, they have equal dimension).
The restriction of $ R _ \lambda ^ {0} $ to the subgroup $ \textrm{SO} ( V, f ) $ is absolutely irreducible, except in the case $ n $ even and $ \lambda = \overline \lambda $ (i.e. the number of terms of $ \lambda $ is equal to $ n/2 $). In the latter case it splits over the field $ k $ or a quadratic extension of it into a sum of two inequivalent absolutely irreducible-representations of equal dimension.
In computing the dimension of $ R _ \lambda ^ {0} $ one can assume that $ \lambda _ {1} ^ \prime \leq n/2 $ (otherwise replace $ \lambda $ by $ \overline \lambda $). Let $ l _ {i} = \lambda _ {i} + n/2 - i $. Then for odd $ n $ one has
$$ \dim R _ \lambda ^ {0} = \ \prod _ {i = 1 } ^ { [ n/2]} \frac{l _ {i} }{n/2 - i } \prod _ {\begin{array}{c} i, j = 1 \\ i < j \end{array} } ^ { [ n/2]} \frac{( l _ {i} - l _ {j} ) ( l _ {i} + l _ {j} ) }{( j - i) ( n - i - j) } , $$
while for even $ n $ and $ \lambda \neq \overline \lambda $ one has
$$ \dim R _ \lambda ^ {0} = \ \prod _ {\begin{array}{c} i, j = 1 \\ i < j \end{array} } ^ { n/2 } \frac{( l _ {i} - l _ {j} ) ( l _ {i} + l _ {j} ) }{( j - i) ( n - i - j) } . $$
For $ \lambda = \overline \lambda $ the latter formula gives half the dimension of $ R _ \lambda ^ {0} $, i.e. the dimension of each of the absolutely-irreducible representations of $ \textrm{SO} ( V, f ) $ corresponding to it.
The decomposition of $ T ^ {m} ( V) $ with respect to the symplectic group $ \textrm{Sp} ( V, f ) $ is analogous to the decomposition with respect to the orthogonal group, with the difference that $ V _ \lambda ^ {0} \neq 0 $ if and only if $ \lambda _ {1} ^ \prime \leq n/2 $. The dimension of $ R _ \lambda ^ {0} $ can in this case be found from
$$ \dim R _ \lambda ^ {0} = \ \prod _ {i = 1 } ^ { n/2 } \frac{l _ {i} }{n/2 - i + 1 } \prod _ {\begin{array}{c} i, j = 1 \\ i < j \end{array} } ^ { n/2 } \frac{( l _ {i} - l _ {j} ) ( l _ {i} + l _ {j} ) }{( j - i) ( n - j - i + 2) } , $$
where $ l _ {i} = \lambda _ {i} - i + 1 + n/2 $.
References
| [1] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) MR0000255 Zbl 1024.20502 |
| [2] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) MR0473097 MR0473098 Zbl 0228.22013 |
| [3] | M. Hamermesh, "Group theory and its application to physical problems" , Addison-Wesley (1962) MR0136667 Zbl 0100.36704 |
Comments
This article describes the classical theory. The contemporary period in this old field of algebra began with [a1]. It can be described by two words: "characteristic-free representation theory" . A different approach to the polynomial representations of $ \textrm{GL} ( V) $ and $ \textrm{SL} ( V) $ was undertaken in [a2]. Further, both classical and characteristic free theories can be found in [a3].
References
| [a1] | R.W. Carter, G. Lustig, "On the modular representations of the general linear and symmetric groups" Math. Z. , 136 (1974) pp. 193–242 MR0369503 MR0354887 Zbl 0301.20005 Zbl 0298.20009 |
| [a2] | J.A. Green, "Polynomial representations of 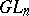 " , Lect. notes in math. , 830 , Springer (1980) MR0606556 Zbl 0451.20037 " , Lect. notes in math. , 830 , Springer (1980) MR0606556 Zbl 0451.20037 |
| [a3] | G. James, A. Kerber, "The representation theory of the symmetric group" , Addison-Wesley (1981) MR0644144 Zbl 0491.20010 |
| [a4] | W. Feit, "The representation theory of finite groups" , North-Holland (1982) MR0661045 Zbl 0493.20007 |
Representation of the classical groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_the_classical_groups&oldid=52296