Difference between revisions of "Integral representations of linear operators"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
m (fixing spaces) |
||
| Line 13: | Line 13: | ||
Let $ ( X, \Lambda, \mu ) $ | Let $ ( X, \Lambda, \mu ) $ | ||
and $ ( Y, \Sigma, \nu ) $ | and $ ( Y, \Sigma, \nu ) $ | ||
| − | be $ \sigma $- | + | be $ \sigma $-finite measure spaces (cf. [[Measure space|Measure space]]) and let $ L _ {0} ( X, \mu ) $ |
| − | finite measure spaces (cf. [[Measure space|Measure space]]) and let $ L _ {0} ( X, \mu ) $ | ||
and $ L _ {0} ( Y, \nu ) $ | and $ L _ {0} ( Y, \nu ) $ | ||
| − | be the spaces of the complex-valued $ \mu $- | + | be the spaces of the complex-valued $ \mu $-measurable functions on $ X $ |
| − | measurable functions on $ X $ | + | and the complex-valued $ \nu $-measurable functions on $ Y $, |
| − | and the complex-valued $ \nu $- | ||
| − | measurable functions on $ Y $, | ||
respectively. A linear subspace $ E = E ( X, \mu ) $ | respectively. A linear subspace $ E = E ( X, \mu ) $ | ||
of $ L _ {0} ( X, \mu ) $ | of $ L _ {0} ( X, \mu ) $ | ||
| Line 26: | Line 23: | ||
$ g \in E $ | $ g \in E $ | ||
and $ | f | \leq | g | $, | and $ | f | \leq | g | $, | ||
| − | $ \mu $- | + | $ \mu $-a.e., imply $ f \in E $. |
| − | a.e., imply $ f \in E $. | + | The classical $ L _ {p} $-spaces ( $ 1 \leq p \leq \infty $), |
| − | The classical $ L _ {p} $- | ||
| − | spaces ( $ 1 \leq p \leq \infty $), | ||
the Orlicz spaces and, more generally, Banach function spaces (cf. also [[Orlicz space|Orlicz space]]; [[Banach space|Banach space]]) are typical examples of normed ideal spaces. | the Orlicz spaces and, more generally, Banach function spaces (cf. also [[Orlicz space|Orlicz space]]; [[Banach space|Banach space]]) are typical examples of normed ideal spaces. | ||
| Line 39: | Line 34: | ||
the linear space of all linear operators from $ E $ | the linear space of all linear operators from $ E $ | ||
into $ F $, | into $ F $, | ||
| − | is called an integral operator, kernel operator, if there exists a $ ( \mu \times \nu ) $- | + | is called an integral operator, kernel operator, if there exists a $ ( \mu \times \nu ) $-measurable function $ T = T ( x,y ) $, |
| − | measurable function $ T = T ( x,y ) $, | ||
$ ( x,y ) \in X \times Y $, | $ ( x,y ) \in X \times Y $, | ||
such that for all $ f \in E $ | such that for all $ f \in E $ | ||
| − | and $ \mu $- | + | and $ \mu $-a.e. with respect to $ x $, |
| − | a.e. with respect to $ x $, | ||
$ ( Tf ) ( x ) = \int _ {Y} {T ( x,y ) f ( y ) } {d \nu ( y ) } $. | $ ( Tf ) ( x ) = \int _ {Y} {T ( x,y ) f ( y ) } {d \nu ( y ) } $. | ||
| Line 55: | Line 48: | ||
$ T \in {\mathcal L} ( E,F ) $ | $ T \in {\mathcal L} ( E,F ) $ | ||
is called a positive linear operator if for all $ 0 \leq f \in E $ | is called a positive linear operator if for all $ 0 \leq f \in E $ | ||
| − | one has $ T f \geq 0 $( | + | one has $ T f \geq 0 $ ($ \mu $-a.e.). An integral operator $ T $ |
| − | $ \mu $- | + | with kernel $ T ( x,y ) $ ($ ( x,y ) \in X \times Y $) |
| − | a.e.). An integral operator $ T $ | ||
| − | with kernel $ T ( x,y ) $( | ||
| − | $ ( x,y ) \in X \times Y $) | ||
is positive if and only if $ T ( x,y ) \geq 0 $, | is positive if and only if $ T ( x,y ) \geq 0 $, | ||
| − | $ ( \mu \times \nu ) $- | + | $ ( \mu \times \nu ) $-a.e.; $ T \in {\mathcal L} ( E,F ) $ |
| − | a.e.; $ T \in {\mathcal L} ( E,F ) $ | ||
is called regular if $ T $ | is called regular if $ T $ | ||
maps order-bounded sets into order-bounded sets, i.e., for all $ f \in E $ | maps order-bounded sets into order-bounded sets, i.e., for all $ f \in E $ | ||
| Line 82: | Line 71: | ||
into $ F $. | into $ F $. | ||
In that case, the kernel of $ | T | $ | In that case, the kernel of $ | T | $ | ||
| − | is given by the modulus $ | {T ( x,y ) } | $( | + | is given by the modulus $ | {T ( x,y ) } | $ ($ ( x,y ) \in X \times Y $) |
| − | $ ( x,y ) \in X \times Y $) | ||
of the kernel of $ T $. | of the kernel of $ T $. | ||
| Line 89: | Line 77: | ||
Integral operators can be characterized via a continuity property: $ T \in {\mathcal L} ( E,F ) $ | Integral operators can be characterized via a continuity property: $ T \in {\mathcal L} ( E,F ) $ | ||
| − | is a linear integral operator if and only if $ 0 \leq f _ {n} \leq f \in E $( | + | is a linear integral operator if and only if $ 0 \leq f _ {n} \leq f \in E $ ($ n = 1,2, \dots $) |
| − | $ n = 1,2, \dots $) | ||
and $ f _ {n} \rightarrow 0 $ | and $ f _ {n} \rightarrow 0 $ | ||
| − | in $ \nu $- | + | in $ \nu $-measure as $ n \rightarrow \infty $ |
| − | measure as $ n \rightarrow \infty $ | + | imply $ Tf _ {n} \rightarrow 0 $ ($ \mu $-a.e.) as $ n \rightarrow \infty $. |
| − | imply $ Tf _ {n} \rightarrow 0 $( | ||
| − | $ \mu $- | ||
| − | a.e.) as $ n \rightarrow \infty $. | ||
| − | An earlier version of this theorem for bilinear forms is due to H. Nakano [[#References|[a4]]]. For regular linear operators defined on KB-spaces (cf. also [[K-space| $ K $- | + | An earlier version of this theorem for bilinear forms is due to H. Nakano [[#References|[a4]]]. For regular linear operators defined on KB-spaces (cf. also [[K-space| $ K $-space]]), the result appeared in a slightly different form in a paper by G.Ya. Lozonovskii [[#References|[a3]]]. The present version is due to A.V. Bukhvalov [[#References|[a1]]]. A pure measure-theoretic proof and related results were given by A. Schep [[#References|[a6]]]. For details and further results see [[#References|[a2]]]. |
| − | space]]), the result appeared in a slightly different form in a paper by G.Ya. Lozonovskii [[#References|[a3]]]. The present version is due to A.V. Bukhvalov [[#References|[a1]]]. A pure measure-theoretic proof and related results were given by A. Schep [[#References|[a6]]]. For details and further results see [[#References|[a2]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.V. Bukhvalov, "A criterion for integral representability of linear operators" ''Funktsional. Anal. i Prilozhen.'' , '''9''' : 1 (1975) pp. 51 (In Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> "Vector lattices and integral operators" S.S. Kutateladze (ed.) , ''Mathematics and its Applications'' , '''358''' , Kluwer Acad. Publ. (1996)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.Ya. Lozanovsky, "On almost integral operators in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i110/i110080/i11008081.png" />-spaces" ''Vestnik Leningrad Gos. Univ.'' , '''7''' (1966) pp. 35–44 (In Russian)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Nakano, "Product spaces of semi-ordered linear spaces" ''J. Fac. Sci. Hokkaidô Univ. Ser. I'' , '''12''' : 3 (1953) pp. 163–210</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. von Neumann, "Charakterisierung des Spektrums eines Integraloperators" , ''Actualités Sc. et Industr.'' , '''229''' , Hermann (1935)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A.R. Schep, "Kernel operators" ''Proc. Kon. Nederl. Akad. Wetensch.'' , '''A 82''' (1979) pp. 39–53</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.V. Bukhvalov, "A criterion for integral representability of linear operators" ''Funktsional. Anal. i Prilozhen.'' , '''9''' : 1 (1975) pp. 51 (In Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> "Vector lattices and integral operators" S.S. Kutateladze (ed.) , ''Mathematics and its Applications'' , '''358''' , Kluwer Acad. Publ. (1996)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.Ya. Lozanovsky, "On almost integral operators in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i110/i110080/i11008081.png" />-spaces" ''Vestnik Leningrad Gos. Univ.'' , '''7''' (1966) pp. 35–44 (In Russian)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Nakano, "Product spaces of semi-ordered linear spaces" ''J. Fac. Sci. Hokkaidô Univ. Ser. I'' , '''12''' : 3 (1953) pp. 163–210</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J. von Neumann, "Charakterisierung des Spektrums eines Integraloperators" , ''Actualités Sc. et Industr.'' , '''229''' , Hermann (1935)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A.R. Schep, "Kernel operators" ''Proc. Kon. Nederl. Akad. Wetensch.'' , '''A 82''' (1979) pp. 39–53</TD></TR></table> | ||
Latest revision as of 16:51, 19 February 2022
Let $ ( X, \Lambda, \mu ) $
and $ ( Y, \Sigma, \nu ) $
be $ \sigma $-finite measure spaces (cf. Measure space) and let $ L _ {0} ( X, \mu ) $
and $ L _ {0} ( Y, \nu ) $
be the spaces of the complex-valued $ \mu $-measurable functions on $ X $
and the complex-valued $ \nu $-measurable functions on $ Y $,
respectively. A linear subspace $ E = E ( X, \mu ) $
of $ L _ {0} ( X, \mu ) $
is called an ideal space, or a solid linear subspace, of $ L _ {0} $
if $ f \in L _ {0} $,
$ g \in E $
and $ | f | \leq | g | $,
$ \mu $-a.e., imply $ f \in E $.
The classical $ L _ {p} $-spaces ( $ 1 \leq p \leq \infty $),
the Orlicz spaces and, more generally, Banach function spaces (cf. also Orlicz space; Banach space) are typical examples of normed ideal spaces.
If $ E $, $ F $ are ideal spaces contained in $ L _ {0} ( Y, \nu ) $ and $ L _ {0} ( X, \mu ) $, respectively, then $ T \in {\mathcal L} ( E,F ) $, the linear space of all linear operators from $ E $ into $ F $, is called an integral operator, kernel operator, if there exists a $ ( \mu \times \nu ) $-measurable function $ T = T ( x,y ) $, $ ( x,y ) \in X \times Y $, such that for all $ f \in E $ and $ \mu $-a.e. with respect to $ x $, $ ( Tf ) ( x ) = \int _ {Y} {T ( x,y ) f ( y ) } {d \nu ( y ) } $.
Integral operators, also known as integral transforms, play an important role in analysis. It is a natural question to ask: Which $ T \in {\mathcal L} ( E,F ) $ are integral operators? J. von Neumann [a5] was the first to show that for the ideal spaces $ E = F = L _ {2} ( [ 0,1 ] ) $ the identity operator does not admit an integral representation. He proved, however, that a bounded self-adjoint linear operator $ T \in {\mathcal L} ( L _ {2} , L _ {2} ) $ is unitarily equivalent (cf. also Unitarily-equivalent operators) to an integral operator if and only if $ 0 $ is an element of the limit spectrum of $ T $.
$ T \in {\mathcal L} ( E,F ) $ is called a positive linear operator if for all $ 0 \leq f \in E $ one has $ T f \geq 0 $ ($ \mu $-a.e.). An integral operator $ T $ with kernel $ T ( x,y ) $ ($ ( x,y ) \in X \times Y $) is positive if and only if $ T ( x,y ) \geq 0 $, $ ( \mu \times \nu ) $-a.e.; $ T \in {\mathcal L} ( E,F ) $ is called regular if $ T $ maps order-bounded sets into order-bounded sets, i.e., for all $ f \in E $ there exists a $ g \in F $ such that for all $ h \in E $ satisfying $ | h | \leq | f | $, one has $ | {Th } | \leq g $; $ T \in {\mathcal L} ( E,F ) $ is ordered bounded if and only if $ T $ can be written as the difference of two positive linear operators if and only if its modulus $ | T | $, where for all $ 0 \leq f \in E $, $ | T | ( f ) = \sup \{ {| {Tg } | } : {| g | \leq f } \} $, is a positive linear operator mapping $ E $ into $ F $.
The following theorem holds: An integral operator $ T \in {\mathcal L} ( E,F ) $ is regular if and only if its modulus $ | T | $ is a positive linear operator mapping $ E $ into $ F $. In that case, the kernel of $ | T | $ is given by the modulus $ | {T ( x,y ) } | $ ($ ( x,y ) \in X \times Y $) of the kernel of $ T $.
An integral transform need not be regular, as is shown, for instance, by the Fourier transform and the Hilbert transform.
Integral operators can be characterized via a continuity property: $ T \in {\mathcal L} ( E,F ) $ is a linear integral operator if and only if $ 0 \leq f _ {n} \leq f \in E $ ($ n = 1,2, \dots $) and $ f _ {n} \rightarrow 0 $ in $ \nu $-measure as $ n \rightarrow \infty $ imply $ Tf _ {n} \rightarrow 0 $ ($ \mu $-a.e.) as $ n \rightarrow \infty $.
An earlier version of this theorem for bilinear forms is due to H. Nakano [a4]. For regular linear operators defined on KB-spaces (cf. also $ K $-space), the result appeared in a slightly different form in a paper by G.Ya. Lozonovskii [a3]. The present version is due to A.V. Bukhvalov [a1]. A pure measure-theoretic proof and related results were given by A. Schep [a6]. For details and further results see [a2].
References
| [a1] | A.V. Bukhvalov, "A criterion for integral representability of linear operators" Funktsional. Anal. i Prilozhen. , 9 : 1 (1975) pp. 51 (In Russian) |
| [a2] | "Vector lattices and integral operators" S.S. Kutateladze (ed.) , Mathematics and its Applications , 358 , Kluwer Acad. Publ. (1996) |
| [a3] | G.Ya. Lozanovsky, "On almost integral operators in 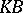 -spaces" Vestnik Leningrad Gos. Univ. , 7 (1966) pp. 35–44 (In Russian) -spaces" Vestnik Leningrad Gos. Univ. , 7 (1966) pp. 35–44 (In Russian) |
| [a4] | H. Nakano, "Product spaces of semi-ordered linear spaces" J. Fac. Sci. Hokkaidô Univ. Ser. I , 12 : 3 (1953) pp. 163–210 |
| [a5] | J. von Neumann, "Charakterisierung des Spektrums eines Integraloperators" , Actualités Sc. et Industr. , 229 , Hermann (1935) |
| [a6] | A.R. Schep, "Kernel operators" Proc. Kon. Nederl. Akad. Wetensch. , A 82 (1979) pp. 39–53 |
Integral representations of linear operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_representations_of_linear_operators&oldid=52081