|
|
| Line 33: |
Line 33: |
| | is called the characteristic polynomial of the LFSR. Using its companion matrix | | is called the characteristic polynomial of the LFSR. Using its companion matrix |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027024.png" /></td> </tr></table>
| + | \begin{equation} |
| | + | A=\left(\begin{array}{cccccc} |
| | + | 0 & 0 & \square & \square & 0 & c_{n} \\ |
| | + | 1 & 0 & \square & \square & 0 & c_{n-1} \\ |
| | + | 0 & 1 & \ddots & \square & \vdots & \vdots \\ |
| | + | \vdots & 0 & \ddots & \ddots & \vdots & \vdots \\ |
| | + | \vdots & \vdots & \square & \ddots & 0 & c_{2} \\ |
| | + | 0 & 0 & \square & \square & 1 & c_{1} |
| | + | \end{array}\right), |
| | + | \end{equation} |
| | | | |
| | the recursion (a2) can be rewritten in terms of the state vectors as | | the recursion (a2) can be rewritten in terms of the state vectors as |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027025.png" /></td> </tr></table>
| + | \begin{equation}\mathbb{a}^{\langle t+1\rangle}=\mathbb{a}^{\langle t\rangle}A\;\text{for}\;t\geq 0\end{equation} |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027026.png" /> is usually called the feedback matrix of the LFSR, and it satisfies the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027027.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027028.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027029.png" /> denote the characteristic and the minimal polynomial of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027030.png" />, respectively.
| + | $A$ is usually called the feedback matrix of the LFSR, and it satisfies the equation $m_A=\chi_A=f^*$, where $\chi_A$ and $m_A$ denote the characteristic and the minimal polynomial of $A$, respectively. |
| | | | |
| − | One may characterize the shift register sequences over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027031.png" /> by associating an arbitrary sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027032.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027033.png" /> with the [[Formal power series|formal power series]] | + | One may characterize the shift register sequences over $F$ by associating an arbitrary sequence $\mathbb{a}=(a_k)$ over $F$ with the [[Formal power series|formal power series]] |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027034.png" /></td> </tr></table>
| + | \begin{equation}a(x)=\sum^{\infty}_{k=0}a_kx^k\in F[[x]]\end{equation} |
| | | | |
| − | Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027035.png" /> is a shift register sequence if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027036.png" /> belongs to the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027037.png" /> of rational functions over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027038.png" />. More precisely, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027039.png" /> can be obtained from the LFSR of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027040.png" /> with feedback polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027041.png" /> if and only if | + | Then $\mathbb{a}$ is a shift register sequence if and only if $a(x)$ belongs to the field $F(x)$ of rational functions over $F$. More precisely, $\mathbb{a}$ can be obtained from the LFSR of length $n$ with feedback polynomial $f\in F[x]$ if and only if |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027042.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a5)</td></tr></table>
| + | \begin{equation}a(x)=\frac{g(x)}{f(x)}\end{equation} |
| | | | |
| − | for a suitable polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027043.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027044.png" />, and this correspondence between shift register sequences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027045.png" /> belonging to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027046.png" /> and polynomials <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027047.png" /> is a bijection. For instance, the Fibonacci sequence, defined by the recursion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027048.png" /> with initial conditions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027049.png" /> over the rational numbers, belongs to the feedback polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027050.png" />, and the polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027051.png" /> is simply <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027052.png" />. Thus, the formal power series describing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027053.png" /> is | + | for a suitable polynomial $g\in F[x]$ with $\deg g<n$, and this correspondence between shift register sequences $\mathbf{a}$ belonging to $f$ and polynomials $g$ is a bijection. For instance, the Fibonacci sequence, defined by the recursion $a_k=a_{k-1}+a_{k+2}$ with initial conditions $(a_0,a_1)=(1,1)$ over the rational numbers, belongs to the feedback polynomial $f(x)=1-x-x^2$, and the polynomial $g(x)$ is simply g(x)=1. Thus, the formal power series describing $\mathbf{a}$ is |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027054.png" /></td> </tr></table>
| + | \begin{equation}a(x)=\frac{1}{1-x-x^2}=1+x+2x^2+3x^3+5x^4+8x^5+13x^6+21x^7+34x^8+...\end{equation} |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027055.png" /></td> </tr></table>
| |
| | | | |
| | (cf. [[Fibonacci numbers|Fibonacci numbers]]). | | (cf. [[Fibonacci numbers|Fibonacci numbers]]). |
| | | | |
| − | There exists a uniquely determined polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027056.png" /> such that a given shift register sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027057.png" /> can be obtained from the LFSR with characteristic polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027058.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027059.png" /> is a multiple of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027060.png" />; this polynomial is called the minimal polynomial of the shift register sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027061.png" />. In other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027062.png" /> is the characteristic polynomial of the linear recurrence relation of least order that is satisfied by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027063.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027064.png" /> belongs to an LFSR of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027065.png" /> with characteristic polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027066.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027067.png" /> is actually the minimal polynomial of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027068.png" /> if and only if the first <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027069.png" /> state vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027070.png" /> are linearly independent. | + | There exists a uniquely determined polynomial $m$ such that a given shift register sequence $\mathbf{a}$ can be obtained from the LFSR with characteristic polynomial $f^*$ if and only if $f^*$ is a multiple of $m$; this polynomial is called the minimal polynomial of the shift register sequence $\mathbf{a}$. In other words, $m$ is the characteristic polynomial of the linear recurrence relation of least order that is satisfied by $\mathbf{a}$. If $\mathbf{a}=(a_k)$ belongs to an LFSR of length $n$ with characteristic polynomial $f^*$, then $f^*$ is actually the minimal polynomial of $\mathbf{a}$ if and only if the first $n$ state vectors $a^{\langle 0\rangle},...,a^{\langle n-1\rangle}$ are linearly independent. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027071.png" /> be a shift register sequence over a [[Galois field|Galois field]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027072.png" /> with minimal polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027073.png" /> of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027074.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027075.png" /> is ultimately periodic with least period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027076.png" /> (cf. [[Ultimately periodic sequence|Ultimately periodic sequence]]). Conversely, any ultimately periodic sequence over a Galois field is in fact a shift register sequence. | + | Let $\mathbf{a}=(a_k)$ be a shift register sequence over a [[Galois field|Galois field]] $F=\text{GF}(q)$ with minimal polynomial $m$ of degree $n$. Then $\mathbf{a}$ is ultimately periodic with least period $r_0\leq q^n-1$ (cf. [[Ultimately periodic sequence|Ultimately periodic sequence]]). Conversely, any ultimately periodic sequence over a Galois field is in fact a shift register sequence. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027077.png" /> belongs to the LFSR with feedback polynomial (a3), where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027078.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027079.png" /> is actually periodic and the feedback matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027080.png" /> is invertible. The particular shift register sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027081.png" /> determined by the initial conditions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027082.png" /> is called the impulse-response sequence for the given LFSR. This name is motivated by thinking of the LFSR of Fig.a1 as being started by sending the "impulse" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027083.png" /> through the left-most cell, where initially each cell is "empty" . The sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027084.png" /> is periodic with least period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027085.png" /> equal to the order of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027086.png" /> (that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027087.png" /> equals the least positive integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027088.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027089.png" />). Moreover, the least period of any shift register sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027090.png" /> which can be obtained from the given LFSR divides <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027091.png" />. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027092.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027093.png" /> is a primitive polynomial for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027094.png" /> (cf. [[Galois field structure|Galois field structure]]). Hence, there exists a periodic shift register sequence with least period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027095.png" /> belonging to an LFSR of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027096.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027097.png" />. Any such sequence is called a maximal period sequence (for short, an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s13027099.png" />-sequence) or a pseudo-noise sequence (for short, a PN-sequence). The latter name stems from the fact that these sequences can be used as pseudo-random sequences for certain engineering applications; indeed, they satisfy the axioms formulated by S.W. Golomb [[#References|[a1]]], cf. also [[#References|[a2]]] and [[Pseudo-random numbers|Pseudo-random numbers]]. The impulse response sequences belonging to LFSRs with primitive feedback polynomials are essentially (up to cyclical equivalence) the only <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270100.png" />-sequences. | + | If $\mathbf{a}=(a_k)$ belongs to the LFSR with feedback polynomial (a3), where $c_n\neq 0$, then $\mathbf{a}$ is actually periodic and the feedback matrix $A$ is invertible. The particular shift register sequence $\mathbf{d}$ determined by the initial conditions $(0,...,0,1)$ is called the impulse-response sequence for the given LFSR. This name is motivated by thinking of the LFSR of Fig.a1 as being started by sending the "impulse" $1$ through the left-most cell, where initially each cell is "empty" . The sequence $\mathbf{d}$ is periodic with least period $r_0$ equal to the order of $A$ (that is, $r_0$ equals the least positive integer $e$ such that $A^e=1$). Moreover, the least period of any shift register sequence $\mathbf{a}$ which can be obtained from the given LFSR divides $r_0$. In particular, $r_0=q^n-1$ if and only if $f$ is a primitive polynomial for $F$ (cf. [[Galois field structure|Galois field structure]]). Hence, there exists a periodic shift register sequence with least period $q^n-1$ belonging to an LFSR of length $n$ over $F=\text{GF}(q)$. Any such sequence is called a maximal period sequence (for short, an $m$-sequence) or a pseudo-noise sequence (for short, a PN-sequence). The latter name stems from the fact that these sequences can be used as pseudo-random sequences for certain engineering applications; indeed, they satisfy the axioms formulated by S.W. Golomb [[#References|[a1]]], cf. also [[#References|[a2]]] and [[Pseudo-random numbers|Pseudo-random numbers]]. The impulse response sequences belonging to LFSRs with primitive feedback polynomials are essentially (up to cyclical equivalence) the only $m$-sequences. |
| | | | |
| − | In the special case of an irreducible feedback polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270101.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270102.png" /> there is an easy explicit description of the associated shift register sequences in terms of the trace function, cf. [[Galois field structure|Galois field structure]]. For this, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270103.png" /> be a root of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270104.png" /> in the extension field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270105.png" />. Then the shift register sequences belonging to the given LFSR are precisely the sequences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270106.png" /> of the form | + | In the special case of an irreducible feedback polynomial $f$ over $F=\text{GF}(q)$ there is an easy explicit description of the associated shift register sequences in terms of the trace function, cf. [[Galois field structure|Galois field structure]]. For this, let $n$ be a root of $f^*$ in the extension field $E=\text{GF}(q^n)$. Then the shift register sequences belonging to the given LFSR are precisely the sequences $\mathbf{s}=(s_k)$ of the form |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270107.png" /></td> </tr></table>
| + | \begin{equation}s_k=\text{Tr}_{E/F}(\theta\;\alpha^k),k\geq 0\end{equation} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270108.png" /> is an arbitrary element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270109.png" />; moreover, the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270110.png" /> is uniquely determined by the sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270111.png" />. Except for the trivial sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270112.png" /> belonging to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270113.png" />, the sequences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270114.png" /> are periodic with least period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270115.png" /> equal to the order of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270116.png" /> (that is, the least positive integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270117.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270118.png" />) and split into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270119.png" /> equivalence classes of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130270/s130270120.png" /> sequences each. | + | where $\theta$ is an arbitrary element of $E$; moreover, the element $\theta$ is uniquely determined by the sequence $\mathbf{s}$. Except for the trivial sequence $\mathbf{0}$ belonging to $\theta=0$, the sequences $\mathbf{s}$ are periodic with least period $r_0$ equal to the order of $\alpha$ (that is, the least positive integer $e$ such that $\alpha^e=1$) and split into $(q^n-1)/r_0$ equivalence classes of $r_0$ sequences each. |
| | | | |
| | While shift register sequences per se are too weak for use in [[Cryptography|cryptography]], suitable (non-linear) combinations of such sequences have been studied in this context, see, e.g., [[#References|[a4]]]. | | While shift register sequences per se are too weak for use in [[Cryptography|cryptography]], suitable (non-linear) combinations of such sequences have been studied in this context, see, e.g., [[#References|[a4]]]. |
recursive sequence, recurrent sequence
A sequence which can be obtained as the output of a linear feedback shift register. The term "shift register sequence" stems from the engineering literature; in mathematics, the terms recursive sequence or recurrent sequence are more common. The classical reference on shift register sequences is [a1]; see also [a2] or [a3] for expositions.
A linear feedback shift register of length $n$ (LFSR) is a time-dependent device (running on a clock) of $n$ cells each capable of holding a value from some field $F$, such that with each clock cycle the contents of the cells are shifted cyclically by one position (to the right, say). While the LFSR discards (or outputs) the rightmost entry $b_0$ (and replaces it by $b_1$), it computes the linear function
\begin{equation}c_1b_{n-1}+...+c_nb_0\end{equation}
of the present state vector $(b_0,...,b_{n-1})$ and the feedback coefficients $(c_1,...,c_n)$, see Fig.a1. Thus, the box with the entry "ADD" stands for an adder over $F$, and the circle with entry $c_i$ indicates multiplication by $c_i\in F$. (The question of how this might be realized in hardware is not addressed here; see [a5], [a6].) In practice, the case of the binary field $\text{GF}(2)$ is by far the most important one, but the general notion of an LFSR serves as a good intuitive way of modelling recursive sequences.
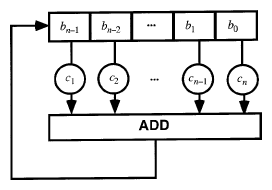
Figure: s130270a
A linear feedback shift register
Given the initial conditions $(a_0,..,a_{n-1})$, after $t$ clock cycles the LFSR will hold the state vector $\mathbf{a}^{\langle t+1\rangle}=(a_t,..,a_{t+n-1})$, where
\begin{equation}a_{t+n-1}=c_1a_{t+n-2}+...+c_na_{t-1}\end{equation}
Thus, the shift register sequence $\mathbf{a}=(a_k)$ produced by the LFSR will satisfy a linear recurrence relation of order $n$; namely, for $k\geq n$:
\begin{equation}a_k=\sum^n_{i=1}c_ia_{k-i}\end{equation}
With the convention $c_0=-1$, one defines the feedback polynomial of the LFSR as
\begin{equation}f(x)=-c_0-...-c_nx^n\end{equation}
its reciprocal polynomial
\begin{equation}f^*(x)=x^n-c_1x^{n-1}-...-c_{n-1}x-c_n\end{equation}
is called the characteristic polynomial of the LFSR. Using its companion matrix
\begin{equation}
A=\left(\begin{array}{cccccc}
0 & 0 & \square & \square & 0 & c_{n} \\
1 & 0 & \square & \square & 0 & c_{n-1} \\
0 & 1 & \ddots & \square & \vdots & \vdots \\
\vdots & 0 & \ddots & \ddots & \vdots & \vdots \\
\vdots & \vdots & \square & \ddots & 0 & c_{2} \\
0 & 0 & \square & \square & 1 & c_{1}
\end{array}\right),
\end{equation}
the recursion (a2) can be rewritten in terms of the state vectors as
\begin{equation}\mathbb{a}^{\langle t+1\rangle}=\mathbb{a}^{\langle t\rangle}A\;\text{for}\;t\geq 0\end{equation}
$A$ is usually called the feedback matrix of the LFSR, and it satisfies the equation $m_A=\chi_A=f^*$, where $\chi_A$ and $m_A$ denote the characteristic and the minimal polynomial of $A$, respectively.
One may characterize the shift register sequences over $F$ by associating an arbitrary sequence $\mathbb{a}=(a_k)$ over $F$ with the formal power series
\begin{equation}a(x)=\sum^{\infty}_{k=0}a_kx^k\in F[[x]]\end{equation}
Then $\mathbb{a}$ is a shift register sequence if and only if $a(x)$ belongs to the field $F(x)$ of rational functions over $F$. More precisely, $\mathbb{a}$ can be obtained from the LFSR of length $n$ with feedback polynomial $f\in F[x]$ if and only if
\begin{equation}a(x)=\frac{g(x)}{f(x)}\end{equation}
for a suitable polynomial $g\in F[x]$ with $\deg g<n$, and this correspondence between shift register sequences $\mathbf{a}$ belonging to $f$ and polynomials $g$ is a bijection. For instance, the Fibonacci sequence, defined by the recursion $a_k=a_{k-1}+a_{k+2}$ with initial conditions $(a_0,a_1)=(1,1)$ over the rational numbers, belongs to the feedback polynomial $f(x)=1-x-x^2$, and the polynomial $g(x)$ is simply g(x)=1. Thus, the formal power series describing $\mathbf{a}$ is
\begin{equation}a(x)=\frac{1}{1-x-x^2}=1+x+2x^2+3x^3+5x^4+8x^5+13x^6+21x^7+34x^8+...\end{equation}
(cf. Fibonacci numbers).
There exists a uniquely determined polynomial $m$ such that a given shift register sequence $\mathbf{a}$ can be obtained from the LFSR with characteristic polynomial $f^*$ if and only if $f^*$ is a multiple of $m$; this polynomial is called the minimal polynomial of the shift register sequence $\mathbf{a}$. In other words, $m$ is the characteristic polynomial of the linear recurrence relation of least order that is satisfied by $\mathbf{a}$. If $\mathbf{a}=(a_k)$ belongs to an LFSR of length $n$ with characteristic polynomial $f^*$, then $f^*$ is actually the minimal polynomial of $\mathbf{a}$ if and only if the first $n$ state vectors $a^{\langle 0\rangle},...,a^{\langle n-1\rangle}$ are linearly independent.
Let $\mathbf{a}=(a_k)$ be a shift register sequence over a Galois field $F=\text{GF}(q)$ with minimal polynomial $m$ of degree $n$. Then $\mathbf{a}$ is ultimately periodic with least period $r_0\leq q^n-1$ (cf. Ultimately periodic sequence). Conversely, any ultimately periodic sequence over a Galois field is in fact a shift register sequence.
If $\mathbf{a}=(a_k)$ belongs to the LFSR with feedback polynomial (a3), where $c_n\neq 0$, then $\mathbf{a}$ is actually periodic and the feedback matrix $A$ is invertible. The particular shift register sequence $\mathbf{d}$ determined by the initial conditions $(0,...,0,1)$ is called the impulse-response sequence for the given LFSR. This name is motivated by thinking of the LFSR of Fig.a1 as being started by sending the "impulse" $1$ through the left-most cell, where initially each cell is "empty" . The sequence $\mathbf{d}$ is periodic with least period $r_0$ equal to the order of $A$ (that is, $r_0$ equals the least positive integer $e$ such that $A^e=1$). Moreover, the least period of any shift register sequence $\mathbf{a}$ which can be obtained from the given LFSR divides $r_0$. In particular, $r_0=q^n-1$ if and only if $f$ is a primitive polynomial for $F$ (cf. Galois field structure). Hence, there exists a periodic shift register sequence with least period $q^n-1$ belonging to an LFSR of length $n$ over $F=\text{GF}(q)$. Any such sequence is called a maximal period sequence (for short, an $m$-sequence) or a pseudo-noise sequence (for short, a PN-sequence). The latter name stems from the fact that these sequences can be used as pseudo-random sequences for certain engineering applications; indeed, they satisfy the axioms formulated by S.W. Golomb [a1], cf. also [a2] and Pseudo-random numbers. The impulse response sequences belonging to LFSRs with primitive feedback polynomials are essentially (up to cyclical equivalence) the only $m$-sequences.
In the special case of an irreducible feedback polynomial $f$ over $F=\text{GF}(q)$ there is an easy explicit description of the associated shift register sequences in terms of the trace function, cf. Galois field structure. For this, let $n$ be a root of $f^*$ in the extension field $E=\text{GF}(q^n)$. Then the shift register sequences belonging to the given LFSR are precisely the sequences $\mathbf{s}=(s_k)$ of the form
\begin{equation}s_k=\text{Tr}_{E/F}(\theta\;\alpha^k),k\geq 0\end{equation}
where $\theta$ is an arbitrary element of $E$; moreover, the element $\theta$ is uniquely determined by the sequence $\mathbf{s}$. Except for the trivial sequence $\mathbf{0}$ belonging to $\theta=0$, the sequences $\mathbf{s}$ are periodic with least period $r_0$ equal to the order of $\alpha$ (that is, the least positive integer $e$ such that $\alpha^e=1$) and split into $(q^n-1)/r_0$ equivalence classes of $r_0$ sequences each.
While shift register sequences per se are too weak for use in cryptography, suitable (non-linear) combinations of such sequences have been studied in this context, see, e.g., [a4].
References
| [a1] | S.W. Golomb, "Shift register sequences" , Aegean Park Press (1982) |
| [a2] | D. Jungnickel, "Finite fields: Structure and arithmetics" , Bibliographisches Inst. Mannheim (1993) |
| [a3] | R. Lidl, H. Niederreiter, "Introduction to finite fields and their applications" , Cambridge Univ. Press (1994) |
| [a4] | R. Rueppel, "Analysis and design of stream ciphers" , Springer (1986) |
| [a5] | U. Tietze, C. Schenk, "Electronic circuits: Design and applications" , Springer (1991) |
| [a6] | N. Weste, K. Eshraghian, "Principles of CMOS VLSI design" , Addison-Wesley (1985) |
