Difference between revisions of "Page theorem"
m (link to Dirichlet L-function) |
(TeX part done) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|part}} | |
| − | + | Page's theorem on the zeros of Dirichlet $L$-functions. | |
| − | + | Let $L(s,\chi)$ be a [[Dirichlet L-function]], $s = \sigma + i t$, with $\chi$ a [[Dirichlet character]] modulo $d$, $d \ge 3$. There are absolute positive constants $c_1,\ldots,c_8$ such that | |
| − | + | a) $L(s,\chi) \ne 0$ for $\sigma > 1 - c_1/\log(dt)$, $t \ge 3$; | |
| − | + | b) $L(s,\chi) \ne 0$ for $\sigma > 1 - c_2/\log(d)$, $0 < t < 5$; | |
| − | + | c) for complex $\chi$ modulo $d$, | |
| + | $$ | ||
| + | L(s,\chi) \ne 0\ \ \text{for}\ \ \sigma > 1 - \frac{c_3}{\log d}\,,\ |t| \le 5\,; | ||
| + | $$ | ||
| − | + | d) for real primitive $\chi$ modulo $d$, | |
| + | $$ | ||
| + | L(s,\chi) \ne 0\ \ \text{for}\ \ \sigma > 1 - \frac{c_4}{\sqrt{d}\log^2 d}\,; | ||
| + | $$ | ||
| − | e) for | + | e) for $2 \le d \le D$ there exists at most one $d=d_0$, $d_0 \ge (\log^2 D)/(\log\log^8 D)$ and at most one real primitive $\psi$ modulo $d$ for which $L(s,\psi$ can have a real zero $\beta_1 > 1- c_6/\log D$, where $\beta_1$ is a simple zero; and for all $\beta$ such that $L(\beta,\psi) =0$, $\beta > 1 - c_6/\log D$ with a real $\psi$ modulo $d$, one has $d \equiv 0 \pmod {d_0}$. |
Page's theorem on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107037.png" />, the number of prime numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107038.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107039.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107040.png" />) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107041.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107042.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107043.png" /> are relatively prime numbers. With the symbols and conditions of Section 1, on account of a)–c) and e) one has | Page's theorem on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107037.png" />, the number of prime numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107038.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107039.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107040.png" />) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107041.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107042.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071070/p07107043.png" /> are relatively prime numbers. With the symbols and conditions of Section 1, on account of a)–c) and e) one has | ||
Revision as of 14:47, 3 July 2020
Page's theorem on the zeros of Dirichlet $L$-functions.
Let $L(s,\chi)$ be a Dirichlet L-function, $s = \sigma + i t$, with $\chi$ a Dirichlet character modulo $d$, $d \ge 3$. There are absolute positive constants $c_1,\ldots,c_8$ such that
a) $L(s,\chi) \ne 0$ for $\sigma > 1 - c_1/\log(dt)$, $t \ge 3$;
b) $L(s,\chi) \ne 0$ for $\sigma > 1 - c_2/\log(d)$, $0 < t < 5$;
c) for complex $\chi$ modulo $d$, $$ L(s,\chi) \ne 0\ \ \text{for}\ \ \sigma > 1 - \frac{c_3}{\log d}\,,\ |t| \le 5\,; $$
d) for real primitive $\chi$ modulo $d$, $$ L(s,\chi) \ne 0\ \ \text{for}\ \ \sigma > 1 - \frac{c_4}{\sqrt{d}\log^2 d}\,; $$
e) for $2 \le d \le D$ there exists at most one $d=d_0$, $d_0 \ge (\log^2 D)/(\log\log^8 D)$ and at most one real primitive $\psi$ modulo $d$ for which $L(s,\psi$ can have a real zero $\beta_1 > 1- c_6/\log D$, where $\beta_1$ is a simple zero; and for all $\beta$ such that $L(\beta,\psi) =0$, $\beta > 1 - c_6/\log D$ with a real $\psi$ modulo $d$, one has $d \equiv 0 \pmod {d_0}$.
Page's theorem on 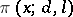 , the number of prime numbers
, the number of prime numbers 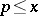 ,
, 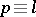 (
(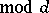 ) for
) for  , where
, where 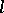 and
and 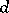 are relatively prime numbers. With the symbols and conditions of Section 1, on account of a)–c) and e) one has
are relatively prime numbers. With the symbols and conditions of Section 1, on account of a)–c) and e) one has
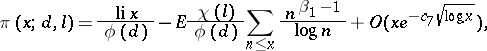 |
where 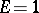 or
or 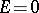 in accordance with whether
in accordance with whether 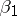 exists or not for a given
exists or not for a given 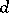 ; because of , for any
; because of , for any 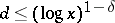 one has for a given
one has for a given 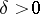 ,
,
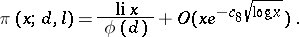 | (*) |
This result is the only one (1983) that is effective in the sense that if 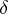 is given, then one can state numerical values of
is given, then one can state numerical values of 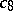 and the constant appearing in the symbol
and the constant appearing in the symbol 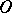 . Replacement of the bound in
. Replacement of the bound in
by the Siegel bound: 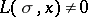 for
for 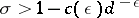 ,
, 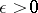 , extends the range of (*) to essentially larger
, extends the range of (*) to essentially larger 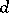 ,
, 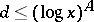 for any fixed
for any fixed  , but the effectiveness of the bound in (*) is lost, since for a given
, but the effectiveness of the bound in (*) is lost, since for a given 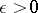 it is impossible to estimate
it is impossible to estimate 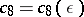 and
and  .
.
A. Page established these theorems in [1].
References
| [1] | A. Page, "On the number of primes in an arithmetic progression" Proc. London Math. Soc. Ser. 2 , 39 : 2 (1935) pp. 116–141 |
| [2] | A.A. Karatsuba, "Fundamentals of analytic number theory" , Moscow (1975) (In Russian) |
| [3] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
Page theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Page_theorem&oldid=50873