Difference between revisions of "Odlyzko bounds"
m (AUTOMATIC EDIT (latexlist): Replaced 26 formulas out of 28 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 28 formulas, 26 were replaced by TEX code.--> | Out of 28 formulas, 26 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
Effective lower bounds for $M ( r _ { 1 } , r _ { 2 } )$, the minimal value of the [[Discriminant|discriminant]] $| d ( K ) |$ of algebraic number fields $K$ having signature $( r _ { 1 } , r _ { 2 } )$ (i.e. having $r_1$ real and $2r_2$ non-real conjugates), obtained in 1976 by A.M. Odlyzko. See also [[Algebraic number|Algebraic number]]; [[Number field|Number field]]. | Effective lower bounds for $M ( r _ { 1 } , r _ { 2 } )$, the minimal value of the [[Discriminant|discriminant]] $| d ( K ) |$ of algebraic number fields $K$ having signature $( r _ { 1 } , r _ { 2 } )$ (i.e. having $r_1$ real and $2r_2$ non-real conjugates), obtained in 1976 by A.M. Odlyzko. See also [[Algebraic number|Algebraic number]]; [[Number field|Number field]]. | ||
Revision as of 17:45, 1 July 2020
Effective lower bounds for $M ( r _ { 1 } , r _ { 2 } )$, the minimal value of the discriminant $| d ( K ) |$ of algebraic number fields $K$ having signature $( r _ { 1 } , r _ { 2 } )$ (i.e. having $r_1$ real and $2r_2$ non-real conjugates), obtained in 1976 by A.M. Odlyzko. See also Algebraic number; Number field.
The first such bound was proved in 1891 by H. Minkowski [a4], who showed
\begin{equation} \tag{a1} M ( r _ { 1 } , r _ { 2 } ) > \left( \frac { \pi } { 4 } \right) ^ { 2 r _ { 2 } } \left( \frac { n ^ { n } } { n ! } \right) ^ { 2 }, \end{equation}
with $n = r _ { 1 } + 2 r _ { 2 }$. He obtained it using methods from the geometry of numbers; the same method was used later by several authors to improve (a1) (see [a5] for the strongest result obtained in this way).
In 1974, H.M. Stark ([a11], [a12]) observed that Hadamard factorization of the Dedekind zeta-function $\zeta _ { K } ( s )$ leads to a formula expressing $\operatorname{log} | d ( K ) |$ by the zeros of $\zeta _ { K } ( s )$ and the value of its logarithmic derivative at a complex number $s _ { 0 } \neq 0,1$ with $\zeta_{ K } ( s _ { 0 } ) \neq 0$. He used this formula with a proper choice of $s_0$ to deduce lower bounds for $M ( r _ { 1 } , r _ { 2 } )$ which were essentially stronger than Minkowski's bound, but did not reach the bounds obtained by geometrical methods.
In 1976, Odlyzko [a7] (cf. [a9]) modified Stark's formula and obtained the following important improvement of (a1):
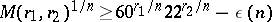 | (a2) |
with $\operatorname { lim } _ { x \rightarrow \infty } \epsilon ( n ) = 0$.
In particular, one has
\begin{equation*} D = \liminf _ { n \rightarrow \infty } M ( r _ { 1 } , r _ { 2 } ) ^ { 1 / n } \geq 22. \end{equation*}
If the extended Riemann hypothesis is assumed (cf. also Riemann hypotheses; Zeta-function), then the constants $60$ and $22$ in (a2) can be replaced by $180$ and $41$, respectively. For small degrees the bound (a2) can be improved (see [a2], [a10]) and several exact values of $M ( r _ { 1 } , r _ { 2 } )$ are known.
On the other hand, it has been shown in [a13], as a consequence of their solution of the class field tower problem (cf. also Tower of fields; Class field theory), that $D$ is finite. The best explicit upper bound for it, $D \leq 92.4$, is due to J. Martinet [a1], who obtained this as a corollary of his constructions of infinite $2$-class towers of suitable fields.
For surveys of this topic, see [a9], [a3] and [a8].
References
| [a1] | J. Martinet, "Tours de corps de classes et estimations de discriminants" Invent. Math. , 44 (1978) pp. 65–73 |
| [a2] | J. Martinet, "Petits discriminants" Ann. Inst. Fourier (Grenoble) , 29 : fasc.1 (1979) pp. 159–170 |
| [a3] | J. Martinet, "Petits discriminants des corps de nombres" , Journ. Arithm. 1980 , Cambridge Univ. Press (1982) pp. 151–193 |
| [a4] | H. Minkowski, "Théorèmes arithmétiques" C.R. Acad. Sci. Paris , 112 (1891) pp. 209–212 (Gesammelte Abh. I (1911), 261-263, Leipzig–Berlin) |
| [a5] | H.P. Mulholland, "On the product of $n$ complex homogeneous linear forms" J. London Math. Soc. , 35 (1960) pp. 241–250 |
| [a6] | A. Odlyzko, "Some analytic estimates of class numbers and discriminants" Invent. Math. , 29 (1975) pp. 275–286 |
| [a7] | A. Odlyzko, "Lower bounds for discriminants of number fields" Acta Arith. , 29 (1976) pp. 275–297 (II: Tôhoku Math. J., 29 (1977), 275-286) |
| [a8] | A. Odlyzko, "Bounds for discriminants and related estimates for class numbers, regulators and zeros of zeta functions: a survey of recent results" Sém. de Théorie des Nombres, Bordeaux , 2 (1990) pp. 119–141 |
| [a9] | G. Poitou, "Minoration de discriminants (d'aprés A.M. Odlyzko)" , Sém. Bourbaki (1975/76) , Lecture Notes in Mathematics , 567 , Springer (1977) pp. 136–153 |
| [a10] | G. Poitou, "Sur les petits discriminants" Sém. Delange–Pisot–Poitou , 18 : 6 (1976/77) |
| [a11] | H.M. Stark, "Some effective cases of the Brauer–Siegel theorem" Invent. Math. , 23 (1974) pp. 135–152 |
| [a12] | H.M. Stark, "The analytic theory of numbers" Bull. Amer. Math. Soc. , 81 (1975) pp. 961–972, |
| [a13] | E.S. Golod, I.R. Shafarevich, "On the class-field tower" Izv. Akad. Nauk. SSSR , 28 (1964) pp. 261–272 (In Russian) |
Odlyzko bounds. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Odlyzko_bounds&oldid=50738