Difference between revisions of "X-inner automorphism"
m (AUTOMATIC EDIT (latexlist): Replaced 114 formulas out of 116 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 116 formulas, 114 were replaced by TEX code.--> | Out of 116 formulas, 114 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
$X$-inner automorphisms were introduced by V.K. Kharchenko in [[#References|[a2]]] and [[#References|[a3]]] to study both prime rings satisfying generalized identities and the Galois theory of semi-prime rings (cf. also [[Prime ring|Prime ring]]; [[Rings and algebras|Rings and algebras]]). Since the appropriate definitions are much simpler when the ring is assumed to be prime, this special case is treated first here. Let $R$ be a [[Prime ring|prime ring]] (with $1$) and let $Q = Q _ { s } ( R )$ denote its symmetric [[Martindale ring of quotients|Martindale ring of quotients]]. Then any [[Automorphism|automorphism]] $\sigma$ of $R$ extends uniquely to an automorphism $\hat { \sigma }$ of $Q$, and one says that $\sigma$ is $X$-inner if $\hat { \sigma }$ is inner on $Q$ (cf. also [[Inner automorphism|Inner automorphism]]). It is easy to see that $\operatorname{Inn} ( R )$, the set of all $X$-inner automorphisms of $R$, is a [[Normal subgroup|normal subgroup]] of $\operatorname{Aut}( R )$. | $X$-inner automorphisms were introduced by V.K. Kharchenko in [[#References|[a2]]] and [[#References|[a3]]] to study both prime rings satisfying generalized identities and the Galois theory of semi-prime rings (cf. also [[Prime ring|Prime ring]]; [[Rings and algebras|Rings and algebras]]). Since the appropriate definitions are much simpler when the ring is assumed to be prime, this special case is treated first here. Let $R$ be a [[Prime ring|prime ring]] (with $1$) and let $Q = Q _ { s } ( R )$ denote its symmetric [[Martindale ring of quotients|Martindale ring of quotients]]. Then any [[Automorphism|automorphism]] $\sigma$ of $R$ extends uniquely to an automorphism $\hat { \sigma }$ of $Q$, and one says that $\sigma$ is $X$-inner if $\hat { \sigma }$ is inner on $Q$ (cf. also [[Inner automorphism|Inner automorphism]]). It is easy to see that $\operatorname{Inn} ( R )$, the set of all $X$-inner automorphisms of $R$, is a [[Normal subgroup|normal subgroup]] of $\operatorname{Aut}( R )$. | ||
Revision as of 17:44, 1 July 2020
$X$-inner automorphisms were introduced by V.K. Kharchenko in [a2] and [a3] to study both prime rings satisfying generalized identities and the Galois theory of semi-prime rings (cf. also Prime ring; Rings and algebras). Since the appropriate definitions are much simpler when the ring is assumed to be prime, this special case is treated first here. Let $R$ be a prime ring (with $1$) and let $Q = Q _ { s } ( R )$ denote its symmetric Martindale ring of quotients. Then any automorphism $\sigma$ of $R$ extends uniquely to an automorphism $\hat { \sigma }$ of $Q$, and one says that $\sigma$ is $X$-inner if $\hat { \sigma }$ is inner on $Q$ (cf. also Inner automorphism). It is easy to see that $\operatorname{Inn} ( R )$, the set of all $X$-inner automorphisms of $R$, is a normal subgroup of $\operatorname{Aut}( R )$.
$X$-inner automorphisms control the generalized linear identities of $R$, namely those linear identities which involve automorphisms. For example, it is shown in [a2] that if $0 \neq a , b , c , d \in R$ and if $\sigma \in \operatorname { Aut } ( R )$ with $a x b = c x ^ { \sigma } d$ for all $x \in R$, then there exists a unit $q \in Q$ with $c = a q$, $d = q ^ { - 1 } b$ and $x ^ { \sigma } = q ^ { - 1 } x q$ for all $x \in R$. In particular, $\hat { \sigma }$ is the inner automorphism of $Q$ induced by $q$ and consequently $\sigma$ is $X$-inner. Of course, $q$ is determined by $\sigma$ up to multiplication by a non-zero element of the extended centroid $C = \mathbf{Z} ( Q ) = \mathbf{C} _ { Q } ( R )$.
Now, let $G$ be a group of automorphisms of $R$ and let $G _ { \text { inn } } = G \cap \operatorname { lnn } ( R )$, so that $G _ { \operatorname{inn} } \triangleleft G$. If $B ( G )$ denotes the linear span of all units $q$ in $Q$ such that conjugation by $q$ belongs to $\hat { G }_{\text{inn}}$, then $B ( G )$ is a $C$-subalgebra of $Q$, called the algebra of the group (cf. also Group algebra). One says that $G$ is an $M$-group (Maschke group) if $|G:G_{\text{inn}}|< \infty$ and if $B ( G )$ is a finite-dimensional semi-simple $C$-algebra. Furthermore, $G$ is an $N$-group (Noether group) if $G$ is an $M$-group and if conjugation by every unit of $B ( G )$ induces an automorphism of $R$ contained in 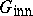 . The Galois theory, as developed in [a3] and [a14], involves the action of $M$-groups and $N$-groups on prime rings.
. The Galois theory, as developed in [a3] and [a14], involves the action of $M$-groups and $N$-groups on prime rings.
Note that if $G$ is an $M$-group and if $q$ is a unit of $B ( G )$, then conjugation by $q$ need not stabilize $R$. Thus, it is not always possible to embed an $M$-group into an $N$-group. One can avoid this difficulty by extending the definition of "automorphism of R" to include those (real) automorphisms $\tau$ of $Q$ such that $\tau ( A ) \subseteq R$ for some $0 \neq A \lhd R$.
$X$-inner automorphisms also appear prominently in the study of cross products. For example, it is proved in [a1] that if $R * G$ is a cross product over the prime ring $R$, then $R * G$ embeds naturally into $S = Q ^ { * } G$ and that $\mathbf{C} _ { S } ( R ) = \mathbf{C} _ { S } ( Q )$ is a twisted group algebra $C ^ { t } [ G _ { \text { inn } } ]$ with $Q ^ { * } G _ { \text { inn } } = Q \otimes _ { C } C ^ { t } [ G _ { \text { inn } } ]$. Furthermore, it is shown in [a9] that every non-zero ideal of $R * G$ meets $R ^ { * } G _ { \text { inn } }$ non-trivially, and in [a11] that $R * G$ is prime (or semi-prime) if and only if $R ^ { * } N$ is $G$-prime (or $G$-semi-prime) for all finite normal subgroups $N$ of $G$ contained in 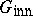 . The above-mentioned structure of $R * G$ is also used in [a5] and [a6] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups.
. The above-mentioned structure of $R * G$ is also used in [a5] and [a6] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups.
There are numerous computations of $\operatorname{Inn} ( R )$ in the literature. To start with, it is shown in [a4] that if $F$ is a non-commutative free algebra, then $\operatorname { lnn } ( F ) = \langle 1 \rangle$. More general free products are studied in [a7] and [a8]. Next, [a10] effectively handles graded domains like enveloping algebras of Lie algebras, and [a15] considers arbitrary enveloping algebra smash products. Finally, [a12] and [a13] study certain group algebras and show that for any group $H$ there exists a domain $R$ with $\operatorname { Aut } ( R ) / \operatorname { lnn } ( R ) \cong H$.
Now suppose that $R$ is a semi-prime ring and again let $Q = Q _ { s } ( R )$ denote its symmetric Martindale ring of quotients. If $\sigma$ is an arbitrary automorphism of $R$, write $\Phi _ { \sigma } = \{ q \in Q : q x ^ { \sigma } = x q \text { for all } x \in R \}$. Then, following [a2], one says that $\sigma$ is $X$-inner if $\Phi _ { \sigma } \neq 0$. Of course, $\sigma$ is $X$-outer when $\Phi _ { \sigma } = 0$. Note that, in the case of semi-prime rings, $\operatorname{Inn} ( R )$ need not be a subgroup of $\operatorname{Aut}( R )$. Nevertheless, a good deal of structure still exists. For example, [a3] proves the key fact that $\Phi _ { \sigma }$ is always a cyclic $C$-module.
References
| [a1] | J.W. Fisher, S. Montgomery, "Semiprime skew group rings" J. Algebra , 52 (1978) pp. 241–247 |
| [a2] | V.K. Kharchenko, "Generalized identities with automorphisms" Algebra and Logic , 14 (1976) pp. 132–148 Algebra i Logika , 14 (1975) pp. 215–237 |
| [a3] | V.K. Kharchenko, "Galois theory of semiprime rings" Algebra and Logic , 16 (1978) pp. 208–258 Algebra i Logika , 16 (1977) pp. 313–363 |
| [a4] | V.K. Kharchenko, "Algebras of invariants of free algebras" Algebra and Logic , 17 (1979) pp. 316–321 Algebra i Logika , 17 (1978) pp. 478–487 |
| [a5] | M. Lorenz, D.S. Passman, "Prime ideals in crossed products of finite groups" Israel J. Math. , 33 (1979) pp. 89–132 |
| [a6] | M. Lorenz, D.S. Passman, "Prime ideals in group algebras of polycyclic-by-finite groups" Proc. London Math. Soc. , 43 (1981) pp. 520–543 |
| [a7] | W.S. Martindale III, "The normal closure of the coproduct of rings over a division ring" Trans. Amer. Math. Soc. , 293 (1986) pp. 303–317 |
| [a8] | W.S. Martindale III, S. Montgomery, "The normal closure of coproducts of domains" J. Algebra , 82 (1983) pp. 1–17 |
| [a9] | S. Montgomery, "Outer automorphisms of semi-prime rings" J. London Math. Soc. , 18 : 2 (1978) pp. 209–220 |
| [a10] | S. Montgomery, "$X$-inner automorphisms of filtered algebras" Proc. Amer. Math. Soc. , 83 (1981) pp. 263–268 |
| [a11] | S. Montgomery, D.S. Passman, "Crossed products over prime rings" Israel J. Math. , 31 (1978) pp. 224–256 |
| [a12] | S. Montgomery, D.S. Passman, "$X$-Inner automorphisms of group rings" Houston J. Math. , 7 (1981) pp. 395–402 |
| [a13] | S. Montgomery, D.S. Passman, "$X$-Inner automorphisms of group rings II" Houston J. Math. , 8 (1982) pp. 537–544 |
| [a14] | S. Montgomery, D.S. Passman, "Galois theory of prime rings" J. Pure Appl. Algebra , 31 (1984) pp. 139–184 |
| [a15] | J. Osterburg, D.S. Passman, "$X$-inner automorphisms of enveloping rings" J. Algebra , 130 (1990) pp. 412–434 |
X-inner automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=X-inner_automorphism&oldid=50681