|
|
| Line 1: |
Line 1: |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b1303001.png" /> be a [[Free group|free group]] of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b1303002.png" />. The free <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b1303003.png" />-generator Burnside group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b1303004.png" /> of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b1303005.png" /> is defined to be the quotient group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b1303006.png" /> by the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b1303007.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b1303008.png" /> generated by all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b1303009.png" />th powers of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030010.png" />. Clearly, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030011.png" /> is the "largest" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030012.png" />-generator group of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030014.png" /> (that is, a group whose elements satisfy the identity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030015.png" />) in the sense that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030016.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030017.png" />-generator group of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030018.png" /> then there exists an epimorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030019.png" />. In 1902, W. Burnside [[#References|[a3]]] posed a problem (which later became known as the Burnside problem for periodic groups) that asks whether every [[Finitely-generated group|finitely-generated group]] of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030020.png" /> is finite, or, equivalently, whether the free Burnside groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030021.png" /> are finite (cf. also [[Burnside problem|Burnside problem]]).
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | It is easy to show that the free <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030022.png" />-generator Burnside group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030023.png" /> of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030024.png" /> is an elementary Abelian 2-group and the order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030025.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030026.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030027.png" />. Burnside showed that the groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030028.png" /> are finite for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030029.png" />. In 1933, F. Levi and B.L. van der Waerden (see [[#References|[a4]]]) proved that the Burnside group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030030.png" /> has the class of nilpotency equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030031.png" />, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030032.png" />, and the order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030033.png" /> equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030034.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030035.png" /> are binomial coefficients. In 1940, I.N. Sanov [[#References|[a18]]] proved that the free Burnside groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030036.png" /> of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030037.png" /> are also finite. In 1954, S.J. Tobin proved that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030038.png" /> (see [[#References|[a4]]]). By making use of computers, A.J. Bayes, J. Kautsky, and J.W. Wamsley showed in 1974 that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030039.png" /> and W.A. Alford, G. Havas and M.F. Newman established in 1975 that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030040.png" /> (see [[#References|[a4]]]). It is also known (see [[#References|[a4]]]) that the class of nilpotency of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030041.png" /> equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030042.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030043.png" />. On the other hand, in 1978, Yu.P. Razmyslov constructed an example of a non-solvable countable group of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030044.png" /> (see [[#References|[a4]]]). In 1958, M. Hall [[#References|[a8]]] proved that the Burnside groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030045.png" /> of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030046.png" /> are finite and have the order given by the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030047.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030048.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030049.png" />.
| + | Out of 179 formulas, 178 were replaced by TEX code.--> |
| | | | |
| − | The attempts to approach the Burnside problem via finite groups gave rise to a restricted version of the Burnside problem (called the restricted Burnside problem) which was stated by W. Magnus [[#References|[a14]]] in 1950 and asks whether there exists a number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030050.png" /> so that the order of any finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030051.png" />-generator group of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030052.png" /> is less than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030053.png" />. The existence of such a bound <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030054.png" /> was proven for prime <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030055.png" /> by A.I. Kostrikin [[#References|[a11]]] in 1959 (see also [[#References|[a12]]]) and for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030056.png" /> with a prime number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030057.png" /> by E.I. Zel'manov [[#References|[a19]]], [[#References|[a20]]] in 1991–1992. It then follows from the Hall–Higman reduction results [[#References|[a6]]] and the classification of finite simple groups that a bound <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030058.png" /> does exist for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030060.png" />.
| + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | Let $F _ { m }$ be a [[Free group|free group]] of rank $m$. The free $m$-generator Burnside group $B ( m , n )$ of exponent $n$ is defined to be the quotient group of $F _ { m }$ by the subgroup $F _ { m } ^ { n }$ of $F _ { m }$ generated by all $n$th powers of elements of $F _ { m }$. Clearly, $B ( m , n )$ is the "largest" $m$-generator group of exponent $n$ (that is, a group whose elements satisfy the identity $x ^ { n } \equiv 1$) in the sense that if $G$ is an $m$-generator group of exponent $n$ then there exists an epimorphism $\phi : B ( m , n ) \rightarrow G$. In 1902, W. Burnside [[#References|[a3]]] posed a problem (which later became known as the Burnside problem for periodic groups) that asks whether every [[Finitely-generated group|finitely-generated group]] of exponent $n$ is finite, or, equivalently, whether the free Burnside groups $B ( m , n )$ are finite (cf. also [[Burnside problem|Burnside problem]]). |
| | | | |
| − | In 1968, P.S. Novikov and S.I. Adyan [[#References|[a15]]] gave a negative solution to the Burnside problem for sufficiently large odd exponents by an explicit construction of infinite free Burnside groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030061.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030062.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030063.png" /> is odd, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030064.png" />, by means of generators and defining relators. See [[#References|[a15]]] for a powerful calculus of periodic words and a large number of lemmas, proved by simultaneous induction. Later, Adyan [[#References|[a1]]] improved on the estimate for the exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030065.png" /> and brought it down to odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030066.png" />. Using their machinery, Novikov and Adyan obtained other results on the free Burnside groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030067.png" />. In particular, the word and conjugacy problems were proved to be solvable for the presentations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030068.png" /> constructed in [[#References|[a15]]], any Abelian or finite subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030069.png" /> was shown to be cyclic (for these and other results, see [[#References|[a1]]]; cf. also [[Identity problem|Identity problem]]; [[Conjugate elements|Conjugate elements]]). | + | It is easy to show that the free $m$-generator Burnside group $B ( m , 2 )$ of exponent $2$ is an elementary Abelian 2-group and the order $| B ( m , 2 ) |$ of $B ( m , 2 )$ is $2 ^ { m }$. Burnside showed that the groups $B ( m , 3 )$ are finite for all $m$. In 1933, F. Levi and B.L. van der Waerden (see [[#References|[a4]]]) proved that the Burnside group $B ( m , 3 )$ has the class of nilpotency equal to $3$, when $m > 3$, and the order $| B ( m , 3 ) |$ equals $3 ^ { C _ { m} ^ { 1 } + C _ { m } ^ { 2 } + C _ { m } ^ { 3 } }$, where $C _ { m } ^ { 1 } , \ldots$ are binomial coefficients. In 1940, I.N. Sanov [[#References|[a18]]] proved that the free Burnside groups $B ( m , 4 )$ of exponent $4$ are also finite. In 1954, S.J. Tobin proved that $| B ( 2,4 ) | = 2 ^ { 12 }$ (see [[#References|[a4]]]). By making use of computers, A.J. Bayes, J. Kautsky, and J.W. Wamsley showed in 1974 that $| B ( 3,4 ) | = 2 ^ { 69 }$ and W.A. Alford, G. Havas and M.F. Newman established in 1975 that $| B ( 4,4 ) | = 2 ^ { 422 }$ (see [[#References|[a4]]]). It is also known (see [[#References|[a4]]]) that the class of nilpotency of $B ( m , 4 )$ equals $3 m - 2$ when $m > 3$. On the other hand, in 1978, Yu.P. Razmyslov constructed an example of a non-solvable countable group of exponent $4$ (see [[#References|[a4]]]). In 1958, M. Hall [[#References|[a8]]] proved that the Burnside groups $B ( m , 6 )$ of exponent $6$ are finite and have the order given by the formula $| B ( m , 6 ) | = 2 ^ { \alpha } 3 ^ { C _ { \beta } ^ { 1 } + C _ { \beta } ^ { 2 } + C _ { \beta } ^ { 3 } }$, where $\alpha = 1 + ( m - 1 ) 3 ^ { C _ { m } ^ { 1 } + C _ { m } ^ { 2 } + C _ { m } ^ { 3 } }$ and $\beta = 1 + ( m - 1 ) 2 ^ { m }$. |
| | | | |
| − | A much simpler construction of free Burnside groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030070.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030071.png" /> and odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030072.png" /> was given by A.Yu. Ol'shanskii [[#References|[a16]]] in 1982 (see also [[#References|[a17]]]). In 1994, further developing Ol'shanskii's geometric method, S.V. Ivanov [[#References|[a9]]] constructed infinite free Burnside groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030073.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030074.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030075.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030076.png" /> is divisible by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030077.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030078.png" /> is even, thus providing a negative solution to the Burnside problem for almost all exponents.
| + | The attempts to approach the Burnside problem via finite groups gave rise to a restricted version of the Burnside problem (called the restricted Burnside problem) which was stated by W. Magnus [[#References|[a14]]] in 1950 and asks whether there exists a number $f ( m , n )$ so that the order of any finite $m$-generator group of exponent $n$ is less than $f ( m , n )$. The existence of such a bound $f ( m , n )$ was proven for prime $n$ by A.I. Kostrikin [[#References|[a11]]] in 1959 (see also [[#References|[a12]]]) and for $n = p ^ { \text{l} }$ with a prime number $p$ by E.I. Zel'manov [[#References|[a19]]], [[#References|[a20]]] in 1991–1992. It then follows from the Hall–Higman reduction results [[#References|[a6]]] and the classification of finite simple groups that a bound $f ( m , n )$ does exist for all $m$ and $n$. |
| | | | |
| − | The construction of free Burnside groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030079.png" /> given in [[#References|[a16]]], [[#References|[a9]]] is based on the following inductive definitions. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030080.png" /> be a free group over an alphabet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030081.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030082.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030083.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030084.png" /> be divisible by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030085.png" /> (from now on these restrictions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030086.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030087.png" /> are assumed, unless otherwise stated; note that this estimate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030088.png" /> was improved on by I.G. Lysenok [[#References|[a13]]] to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030089.png" /> in 1996). By induction on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030090.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030091.png" /> and, assuming that the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030092.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030093.png" /> is already constructed as a quotient group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030094.png" />, define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030095.png" /> to be a shortest element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030096.png" /> (if any) the order of whose image (under the natural epimorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030097.png" />) is infinite. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030098.png" /> is constructed as a quotient group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b13030099.png" /> by the normal closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300100.png" />. Clearly, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300101.png" /> has a presentation of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300102.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300103.png" /> are the defining relators of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300104.png" />. It is proven in [[#References|[a9]]] (and in [[#References|[a16]]] for odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300105.png" />) that for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300106.png" /> the word <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300107.png" /> does exist. Furthermore, it is shown in [[#References|[a9]]] (and in [[#References|[a16]]] for odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300108.png" />) that the direct limit <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300109.png" /> of the groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300110.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300111.png" /> (obtained by imposing on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300112.png" /> of relators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300113.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300114.png" />) is exactly the free <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300115.png" />-generator Burnside group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300116.png" /> of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300117.png" />. The infiniteness of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300118.png" /> already follows from the existence of the word <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300119.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300120.png" />, since, otherwise, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300121.png" /> could be given by finitely many relators and so <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300122.png" /> would fail to exist for sufficiently large <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300123.png" />. It is also shown in [[#References|[a9]]] that the word and conjugacy problems for the constructed presentation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300124.png" /> are solvable. In fact, these decision problems are effectively reduced to the word problem for groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300125.png" /> and it is shown that each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300126.png" /> satisfies a linear isoperimetric inequality and hence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300127.png" /> is a Gromov hyperbolic group [[#References|[a5]]] (cf. [[Hyperbolic group|Hyperbolic group]]).
| + | In 1968, P.S. Novikov and S.I. Adyan [[#References|[a15]]] gave a negative solution to the Burnside problem for sufficiently large odd exponents by an explicit construction of infinite free Burnside groups $B ( m , n )$, where $m \geq 2$ and $n$ is odd, $n\geq 4381$, by means of generators and defining relators. See [[#References|[a15]]] for a powerful calculus of periodic words and a large number of lemmas, proved by simultaneous induction. Later, Adyan [[#References|[a1]]] improved on the estimate for the exponent $n$ and brought it down to odd $n\geq 665$. Using their machinery, Novikov and Adyan obtained other results on the free Burnside groups $B ( m , n )$. In particular, the word and conjugacy problems were proved to be solvable for the presentations of $B ( m , n )$ constructed in [[#References|[a15]]], any Abelian or finite subgroup of $B ( m , n )$ was shown to be cyclic (for these and other results, see [[#References|[a1]]]; cf. also [[Identity problem|Identity problem]]; [[Conjugate elements|Conjugate elements]]). |
| | | | |
| − | It should be noted that the structure of finite subgroups of the groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300128.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300129.png" /> is very complex when the exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300130.png" /> is even and, in fact, finite subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300131.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300132.png" /> play a key role in proofs in [[#References|[a9]]] (which, like [[#References|[a15]]], also contains a large number of lemmas, proved by simultaneous induction). The central result related to finite subgroups of the groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300133.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300134.png" /> is the following: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300135.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300136.png" /> is the maximal odd divisor of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300137.png" />. Then any finite subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300138.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300139.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300140.png" /> is isomorphic to a subgroup of the direct product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300141.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300142.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300143.png" /> denotes a dihedral group of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300144.png" />. The principal difference between odd and even exponents in the Burnside problem can be illustrated by pointing out that, on the one hand, for every odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300145.png" /> there are infinite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300146.png" />-generator groups of exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300147.png" /> all of whose proper subgroups are cyclic (as was proved in [[#References|[a2]]], see also [[#References|[a17]]]) and, on the other hand, any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300148.png" />-group the orders of whose Abelian (or finite) subgroups are bounded is itself finite (see [[#References|[a7]]]).
| + | A much simpler construction of free Burnside groups $B ( m , n )$ for $m > 1$ and odd $n > 10 ^ { 10 }$ was given by A.Yu. Ol'shanskii [[#References|[a16]]] in 1982 (see also [[#References|[a17]]]). In 1994, further developing Ol'shanskii's geometric method, S.V. Ivanov [[#References|[a9]]] constructed infinite free Burnside groups $B ( m , n )$, where $m > 1$, $n \geq 2 ^ { 48 }$ and $n$ is divisible by $2 ^ { 9 }$ if $n$ is even, thus providing a negative solution to the Burnside problem for almost all exponents. |
| | | | |
| − | In 1997, Ivanov and Ol'shanskii [[#References|[a10]]] showed that the above description of finite subgroups in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300149.png" /> is complete (that is, every subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300150.png" /> can actually be found in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300151.png" />) and obtained the following result: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300152.png" /> be a finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300153.png" />-subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300154.png" />. Then the centralizer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300155.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300156.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300157.png" /> contains a subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300158.png" /> isomorphic to a free Burnside group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300159.png" /> of infinite countable rank such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300160.png" />, whence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300161.png" />. (Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300162.png" /> obviously contains subgroups isomorphic to both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300163.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300164.png" />, an embedding of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300165.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300166.png" /> becomes trivial.) Among other results on subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300167.png" /> proven in [[#References|[a10]]] are the following: The centralizer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300168.png" /> of a subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300169.png" /> is infinite if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300170.png" /> is a locally finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300171.png" />-group. Any infinite locally finite subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300172.png" /> is contained in a unique maximal locally finite subgroup while any finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300173.png" />-subgroup is contained in continuously many pairwise non-isomorphic maximal locally finite subgroups. A complete description of infinite (maximal) locally finite subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300174.png" /> has also been obtained, in [[#References|[a10]]]. | + | The construction of free Burnside groups $B ( m , n )$ given in [[#References|[a16]]], [[#References|[a9]]] is based on the following inductive definitions. Let $F _ { m }$ be a free group over an alphabet $\mathcal{A} = \{ a _ { 1 } ^ { \pm 1 } , \ldots , a _ { m } ^ { \pm 1 } \}$, $m > 1$, let $n \geq 2 ^ { 48 }$ and let $n$ be divisible by $2 ^ { 9 }$ (from now on these restrictions on $m$ and $n$ are assumed, unless otherwise stated; note that this estimate $n \geq 2 ^ { 48 }$ was improved on by I.G. Lysenok [[#References|[a13]]] to $n \geq 2 ^ { 13 }$ in 1996). By induction on $i$, let $B ( m , n , 0 ) = F _ { m }$ and, assuming that the group $B ( m , n , i - 1 )$ with $i \geq 1$ is already constructed as a quotient group of $F _ { m }$, define $A_i$ to be a shortest element of $F _ { m }$ (if any) the order of whose image (under the natural epimorphism $\psi _ { i - 1 } : F _ { m } \rightarrow B ( m , n , i - 1 )$) is infinite. Then $B ( m , n , i )$ is constructed as a quotient group of $B ( m , n , i - 1 )$ by the normal closure of $\psi _ { i - 1 } ( A _ { i } ^ { n } )$. Clearly, $B ( m , n , i )$ has a presentation of the form $B ( m , n , i ) = \langle a _ { 1 } , \dots , a _ { m } | A _ { 1 } ^ { n } , \dots , A _ { i } ^ { n } \rangle$, where $A _ { 1 } ^ { n } , \dots , A _ { i } ^ { n }$ are the defining relators of $B ( m , n , i )$. It is proven in [[#References|[a9]]] (and in [[#References|[a16]]] for odd $n > 10 ^ { 10 }$) that for every $i$ the word $A_i$ does exist. Furthermore, it is shown in [[#References|[a9]]] (and in [[#References|[a16]]] for odd $n > 10 ^ { 10 }$) that the direct limit $B ( m , n , \infty )$ of the groups $B ( m , n , i )$ as $i \rightarrow \infty$ (obtained by imposing on $F _ { m }$ of relators $A_{i}^{n}$ for all $i = 1,2 , \dots$) is exactly the free $m$-generator Burnside group $B ( m , n )$ of exponent $n$. The infiniteness of the group $B ( m , n )$ already follows from the existence of the word $A_i$ for every $i \geq 1$, since, otherwise, $B ( m , n )$ could be given by finitely many relators and so $A_i$ would fail to exist for sufficiently large $i$. It is also shown in [[#References|[a9]]] that the word and conjugacy problems for the constructed presentation of $B ( m , n )$ are solvable. In fact, these decision problems are effectively reduced to the word problem for groups $B ( m , n , i )$ and it is shown that each $B ( m , n , i )$ satisfies a linear isoperimetric inequality and hence $B ( m , n , i )$ is a Gromov hyperbolic group [[#References|[a5]]] (cf. [[Hyperbolic group|Hyperbolic group]]). |
| | + | |
| | + | It should be noted that the structure of finite subgroups of the groups $B ( m , n , i )$, $B ( m , n )$ is very complex when the exponent $n$ is even and, in fact, finite subgroups of $B ( m , n , i )$, $B ( m , n )$ play a key role in proofs in [[#References|[a9]]] (which, like [[#References|[a15]]], also contains a large number of lemmas, proved by simultaneous induction). The central result related to finite subgroups of the groups $B ( m , n , i )$, $B ( m , n )$ is the following: Let $n = n _ { 1 } n _ { 2 }$, where $n_ 1$ is the maximal odd divisor of $n$. Then any finite subgroup $G$ of $B ( m , n , i )$, $B ( m , n )$ is isomorphic to a subgroup of the direct product $D ( 2 n_1 ) \times D ( 2 n_2 ) ^ { \text{l} }$ for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300142.png"/>, where $D ( 2 k )$ denotes a dihedral group of order $2 k$. The principal difference between odd and even exponents in the Burnside problem can be illustrated by pointing out that, on the one hand, for every odd $n \gg 1$ there are infinite $2$-generator groups of exponent $n$ all of whose proper subgroups are cyclic (as was proved in [[#References|[a2]]], see also [[#References|[a17]]]) and, on the other hand, any $2$-group the orders of whose Abelian (or finite) subgroups are bounded is itself finite (see [[#References|[a7]]]). |
| | + | |
| | + | In 1997, Ivanov and Ol'shanskii [[#References|[a10]]] showed that the above description of finite subgroups in $B ( m , n )$ is complete (that is, every subgroup of $D ( 2 n_1 ) \times D ( 2 n_2 ) ^ { \text{l} }$ can actually be found in $B ( m , n )$) and obtained the following result: Let $G$ be a finite $2$-subgroup of $B ( m , n )$. Then the centralizer $C_{B ( m , n )} ( G )$ of $G$ in $B ( m , n )$ contains a subgroup $B$ isomorphic to a free Burnside group $B ( \infty , n )$ of infinite countable rank such that $G \cap B = \{ 1 \}$, whence $\langle G , B \rangle = G \times B$. (Since $B ( \infty , n )$ obviously contains subgroups isomorphic to both $D ( 2 n _ { 1 } )$ and $D ( 2 n _ { 2 } )$, an embedding of $D ( 2 n_1 ) \times D ( 2 n_2 ) ^ { \text{l} }$ in $B ( m , n )$ becomes trivial.) Among other results on subgroups of $B ( m , n )$ proven in [[#References|[a10]]] are the following: The centralizer $C _ { B ( m , n ) } ( S )$ of a subgroup $S$ is infinite if and only if $S$ is a locally finite $2$-group. Any infinite locally finite subgroup $L$ is contained in a unique maximal locally finite subgroup while any finite $2$-subgroup is contained in continuously many pairwise non-isomorphic maximal locally finite subgroups. A complete description of infinite (maximal) locally finite subgroups of $B ( m , n )$ has also been obtained, in [[#References|[a10]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.I. Adian, "The Burnside problems and identities in groups" , Springer (1979) (In Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.S. Atabekian, S.V. Ivanov, "Two remarks on groups of bounded exponent" , '''2243-B87''' , VINITI, Moscow (1987) ((This is kept in the Depot of VINITI, Moscow, and is available upon request))</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Burnside, "An unsettled question in the theory of discontinuous groups" ''Quart. J. Pure Appl. Math.'' , '''33''' (1902) pp. 230–238</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> N. Gupta, "On groups in which every element has finite order" ''Amer. Math. Monthly'' , '''96''' (1989) pp. 297–308</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Gromov, "Hyperbolic groups" S.M. Gersten (ed.) , ''Essays in Group Theory'' , Springer (1987) pp. 75–263</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> Ph. Hall, G. Higman, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300175.png" />-length of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300176.png" />-soluble groups and reduction theorems for Burnside's problem" ''Proc. London Math. Soc.'' , '''6''' (1956) pp. 1–42</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D. Held, "On abelian subgroups of an infinite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300177.png" />-group" ''Acta Sci. Math. (Szeged)'' , '''27''' (1966) pp. 97–98</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> M. Hall Jr., "Solution of the Burnside problem for exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300178.png" />" ''Proc. Nat. Acad. Sci. USA'' , '''43''' (1957) pp. 751–753</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> S.V. Ivanov, "The free Burnside groups of sufficiently large exponents" ''Internat. J. Algebra Comput.'' , '''4''' (1994) pp. 1–308</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> S.V. Ivanov, A.Yu. Ol'shanskii, "On finite and locally finite subgroups of free Burnside groups of large even exponents" ''J. Algebra'' , '''195''' (1997) pp. 241–284</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> A.I. Kostrikin, "On the Burnside problem" ''Math. USSR Izv.'' , '''23''' (1959) pp. 3–34 (In Russian)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> A.I. Kostrikin, "Around Burnside" , Nauka (1986) (In Russian)</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> I.G. Lysenok, "Infinite Burnside groups of even period" ''Math. Ross. Izv.'' , '''60''' (1996) pp. 3–224</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> W. Magnus, "A connection between the Baker–Hausdorff formula and a problem of Burnside" ''Ann. Math.'' , '''52''' (1950) pp. 11–26 (Also: 57 (1953), 606)</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> P.S. Novikov, S.I. Adian, "On infinite periodic groups I–III" ''Math. USSR Izv.'' , '''32''' (1968) pp. 212–244; 251–524; 709–731</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> A.Yu. Ol'shanskii, "On the Novikov–Adian theorem" ''Math. USSR Sb.'' , '''118''' (1982) pp. 203–235 (In Russian)</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> A.Yu. Ol'shanskii, "Geometry of defining relations in groups" , Kluwer Acad. Publ. (1991) (In Russian)</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> I.N. Sanov, "Solution of the Burnside problem for exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300179.png" />" ''Uch. Zapiski Leningrad State Univ. Ser. Mat.'' , '''10''' (1940) pp. 166–170</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> E.I. Zel'manov, "Solution of the restricted Burnside problem for groups of odd exponent" ''Math. USSR Izv.'' , '''36''' (1991) pp. 41–60 (In Russian)</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> E.I. Zel'manov, "A solution of the restricted Burnside problem for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130300/b130300180.png" />-groups" ''Math. USSR Sb.'' , '''72''' (1992) pp. 543–565 (In Russian)</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> S.I. Adian, "The Burnside problems and identities in groups" , Springer (1979) (In Russian)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> V.S. Atabekian, S.V. Ivanov, "Two remarks on groups of bounded exponent" , '''2243-B87''' , VINITI, Moscow (1987) ((This is kept in the Depot of VINITI, Moscow, and is available upon request))</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> W. Burnside, "An unsettled question in the theory of discontinuous groups" ''Quart. J. Pure Appl. Math.'' , '''33''' (1902) pp. 230–238</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> N. Gupta, "On groups in which every element has finite order" ''Amer. Math. Monthly'' , '''96''' (1989) pp. 297–308</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M. Gromov, "Hyperbolic groups" S.M. Gersten (ed.) , ''Essays in Group Theory'' , Springer (1987) pp. 75–263</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> Ph. Hall, G. Higman, "On the $p$-length of $p$-soluble groups and reduction theorems for Burnside's problem" ''Proc. London Math. Soc.'' , '''6''' (1956) pp. 1–42</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> D. Held, "On abelian subgroups of an infinite $2$-group" ''Acta Sci. Math. (Szeged)'' , '''27''' (1966) pp. 97–98</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> M. Hall Jr., "Solution of the Burnside problem for exponent $6$" ''Proc. Nat. Acad. Sci. USA'' , '''43''' (1957) pp. 751–753</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> S.V. Ivanov, "The free Burnside groups of sufficiently large exponents" ''Internat. J. Algebra Comput.'' , '''4''' (1994) pp. 1–308</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> S.V. Ivanov, A.Yu. Ol'shanskii, "On finite and locally finite subgroups of free Burnside groups of large even exponents" ''J. Algebra'' , '''195''' (1997) pp. 241–284</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> A.I. Kostrikin, "On the Burnside problem" ''Math. USSR Izv.'' , '''23''' (1959) pp. 3–34 (In Russian)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> A.I. Kostrikin, "Around Burnside" , Nauka (1986) (In Russian)</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> I.G. Lysenok, "Infinite Burnside groups of even period" ''Math. Ross. Izv.'' , '''60''' (1996) pp. 3–224</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> W. Magnus, "A connection between the Baker–Hausdorff formula and a problem of Burnside" ''Ann. Math.'' , '''52''' (1950) pp. 11–26 (Also: 57 (1953), 606)</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> P.S. Novikov, S.I. Adian, "On infinite periodic groups I–III" ''Math. USSR Izv.'' , '''32''' (1968) pp. 212–244; 251–524; 709–731</td></tr><tr><td valign="top">[a16]</td> <td valign="top"> A.Yu. Ol'shanskii, "On the Novikov–Adian theorem" ''Math. USSR Sb.'' , '''118''' (1982) pp. 203–235 (In Russian)</td></tr><tr><td valign="top">[a17]</td> <td valign="top"> A.Yu. Ol'shanskii, "Geometry of defining relations in groups" , Kluwer Acad. Publ. (1991) (In Russian)</td></tr><tr><td valign="top">[a18]</td> <td valign="top"> I.N. Sanov, "Solution of the Burnside problem for exponent $4$" ''Uch. Zapiski Leningrad State Univ. Ser. Mat.'' , '''10''' (1940) pp. 166–170</td></tr><tr><td valign="top">[a19]</td> <td valign="top"> E.I. Zel'manov, "Solution of the restricted Burnside problem for groups of odd exponent" ''Math. USSR Izv.'' , '''36''' (1991) pp. 41–60 (In Russian)</td></tr><tr><td valign="top">[a20]</td> <td valign="top"> E.I. Zel'manov, "A solution of the restricted Burnside problem for $2$-groups" ''Math. USSR Sb.'' , '''72''' (1992) pp. 543–565 (In Russian)</td></tr></table> |
Let $F _ { m }$ be a free group of rank $m$. The free $m$-generator Burnside group $B ( m , n )$ of exponent $n$ is defined to be the quotient group of $F _ { m }$ by the subgroup $F _ { m } ^ { n }$ of $F _ { m }$ generated by all $n$th powers of elements of $F _ { m }$. Clearly, $B ( m , n )$ is the "largest" $m$-generator group of exponent $n$ (that is, a group whose elements satisfy the identity $x ^ { n } \equiv 1$) in the sense that if $G$ is an $m$-generator group of exponent $n$ then there exists an epimorphism $\phi : B ( m , n ) \rightarrow G$. In 1902, W. Burnside [a3] posed a problem (which later became known as the Burnside problem for periodic groups) that asks whether every finitely-generated group of exponent $n$ is finite, or, equivalently, whether the free Burnside groups $B ( m , n )$ are finite (cf. also Burnside problem).
It is easy to show that the free $m$-generator Burnside group $B ( m , 2 )$ of exponent $2$ is an elementary Abelian 2-group and the order $| B ( m , 2 ) |$ of $B ( m , 2 )$ is $2 ^ { m }$. Burnside showed that the groups $B ( m , 3 )$ are finite for all $m$. In 1933, F. Levi and B.L. van der Waerden (see [a4]) proved that the Burnside group $B ( m , 3 )$ has the class of nilpotency equal to $3$, when $m > 3$, and the order $| B ( m , 3 ) |$ equals $3 ^ { C _ { m} ^ { 1 } + C _ { m } ^ { 2 } + C _ { m } ^ { 3 } }$, where $C _ { m } ^ { 1 } , \ldots$ are binomial coefficients. In 1940, I.N. Sanov [a18] proved that the free Burnside groups $B ( m , 4 )$ of exponent $4$ are also finite. In 1954, S.J. Tobin proved that $| B ( 2,4 ) | = 2 ^ { 12 }$ (see [a4]). By making use of computers, A.J. Bayes, J. Kautsky, and J.W. Wamsley showed in 1974 that $| B ( 3,4 ) | = 2 ^ { 69 }$ and W.A. Alford, G. Havas and M.F. Newman established in 1975 that $| B ( 4,4 ) | = 2 ^ { 422 }$ (see [a4]). It is also known (see [a4]) that the class of nilpotency of $B ( m , 4 )$ equals $3 m - 2$ when $m > 3$. On the other hand, in 1978, Yu.P. Razmyslov constructed an example of a non-solvable countable group of exponent $4$ (see [a4]). In 1958, M. Hall [a8] proved that the Burnside groups $B ( m , 6 )$ of exponent $6$ are finite and have the order given by the formula $| B ( m , 6 ) | = 2 ^ { \alpha } 3 ^ { C _ { \beta } ^ { 1 } + C _ { \beta } ^ { 2 } + C _ { \beta } ^ { 3 } }$, where $\alpha = 1 + ( m - 1 ) 3 ^ { C _ { m } ^ { 1 } + C _ { m } ^ { 2 } + C _ { m } ^ { 3 } }$ and $\beta = 1 + ( m - 1 ) 2 ^ { m }$.
The attempts to approach the Burnside problem via finite groups gave rise to a restricted version of the Burnside problem (called the restricted Burnside problem) which was stated by W. Magnus [a14] in 1950 and asks whether there exists a number $f ( m , n )$ so that the order of any finite $m$-generator group of exponent $n$ is less than $f ( m , n )$. The existence of such a bound $f ( m , n )$ was proven for prime $n$ by A.I. Kostrikin [a11] in 1959 (see also [a12]) and for $n = p ^ { \text{l} }$ with a prime number $p$ by E.I. Zel'manov [a19], [a20] in 1991–1992. It then follows from the Hall–Higman reduction results [a6] and the classification of finite simple groups that a bound $f ( m , n )$ does exist for all $m$ and $n$.
In 1968, P.S. Novikov and S.I. Adyan [a15] gave a negative solution to the Burnside problem for sufficiently large odd exponents by an explicit construction of infinite free Burnside groups $B ( m , n )$, where $m \geq 2$ and $n$ is odd, $n\geq 4381$, by means of generators and defining relators. See [a15] for a powerful calculus of periodic words and a large number of lemmas, proved by simultaneous induction. Later, Adyan [a1] improved on the estimate for the exponent $n$ and brought it down to odd $n\geq 665$. Using their machinery, Novikov and Adyan obtained other results on the free Burnside groups $B ( m , n )$. In particular, the word and conjugacy problems were proved to be solvable for the presentations of $B ( m , n )$ constructed in [a15], any Abelian or finite subgroup of $B ( m , n )$ was shown to be cyclic (for these and other results, see [a1]; cf. also Identity problem; Conjugate elements).
A much simpler construction of free Burnside groups $B ( m , n )$ for $m > 1$ and odd $n > 10 ^ { 10 }$ was given by A.Yu. Ol'shanskii [a16] in 1982 (see also [a17]). In 1994, further developing Ol'shanskii's geometric method, S.V. Ivanov [a9] constructed infinite free Burnside groups $B ( m , n )$, where $m > 1$, $n \geq 2 ^ { 48 }$ and $n$ is divisible by $2 ^ { 9 }$ if $n$ is even, thus providing a negative solution to the Burnside problem for almost all exponents.
The construction of free Burnside groups $B ( m , n )$ given in [a16], [a9] is based on the following inductive definitions. Let $F _ { m }$ be a free group over an alphabet $\mathcal{A} = \{ a _ { 1 } ^ { \pm 1 } , \ldots , a _ { m } ^ { \pm 1 } \}$, $m > 1$, let $n \geq 2 ^ { 48 }$ and let $n$ be divisible by $2 ^ { 9 }$ (from now on these restrictions on $m$ and $n$ are assumed, unless otherwise stated; note that this estimate $n \geq 2 ^ { 48 }$ was improved on by I.G. Lysenok [a13] to $n \geq 2 ^ { 13 }$ in 1996). By induction on $i$, let $B ( m , n , 0 ) = F _ { m }$ and, assuming that the group $B ( m , n , i - 1 )$ with $i \geq 1$ is already constructed as a quotient group of $F _ { m }$, define $A_i$ to be a shortest element of $F _ { m }$ (if any) the order of whose image (under the natural epimorphism $\psi _ { i - 1 } : F _ { m } \rightarrow B ( m , n , i - 1 )$) is infinite. Then $B ( m , n , i )$ is constructed as a quotient group of $B ( m , n , i - 1 )$ by the normal closure of $\psi _ { i - 1 } ( A _ { i } ^ { n } )$. Clearly, $B ( m , n , i )$ has a presentation of the form $B ( m , n , i ) = \langle a _ { 1 } , \dots , a _ { m } | A _ { 1 } ^ { n } , \dots , A _ { i } ^ { n } \rangle$, where $A _ { 1 } ^ { n } , \dots , A _ { i } ^ { n }$ are the defining relators of $B ( m , n , i )$. It is proven in [a9] (and in [a16] for odd $n > 10 ^ { 10 }$) that for every $i$ the word $A_i$ does exist. Furthermore, it is shown in [a9] (and in [a16] for odd $n > 10 ^ { 10 }$) that the direct limit $B ( m , n , \infty )$ of the groups $B ( m , n , i )$ as $i \rightarrow \infty$ (obtained by imposing on $F _ { m }$ of relators $A_{i}^{n}$ for all $i = 1,2 , \dots$) is exactly the free $m$-generator Burnside group $B ( m , n )$ of exponent $n$. The infiniteness of the group $B ( m , n )$ already follows from the existence of the word $A_i$ for every $i \geq 1$, since, otherwise, $B ( m , n )$ could be given by finitely many relators and so $A_i$ would fail to exist for sufficiently large $i$. It is also shown in [a9] that the word and conjugacy problems for the constructed presentation of $B ( m , n )$ are solvable. In fact, these decision problems are effectively reduced to the word problem for groups $B ( m , n , i )$ and it is shown that each $B ( m , n , i )$ satisfies a linear isoperimetric inequality and hence $B ( m , n , i )$ is a Gromov hyperbolic group [a5] (cf. Hyperbolic group).
It should be noted that the structure of finite subgroups of the groups $B ( m , n , i )$, $B ( m , n )$ is very complex when the exponent $n$ is even and, in fact, finite subgroups of $B ( m , n , i )$, $B ( m , n )$ play a key role in proofs in [a9] (which, like [a15], also contains a large number of lemmas, proved by simultaneous induction). The central result related to finite subgroups of the groups $B ( m , n , i )$, $B ( m , n )$ is the following: Let $n = n _ { 1 } n _ { 2 }$, where $n_ 1$ is the maximal odd divisor of $n$. Then any finite subgroup $G$ of $B ( m , n , i )$, $B ( m , n )$ is isomorphic to a subgroup of the direct product $D ( 2 n_1 ) \times D ( 2 n_2 ) ^ { \text{l} }$ for some 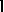 , where $D ( 2 k )$ denotes a dihedral group of order $2 k$. The principal difference between odd and even exponents in the Burnside problem can be illustrated by pointing out that, on the one hand, for every odd $n \gg 1$ there are infinite $2$-generator groups of exponent $n$ all of whose proper subgroups are cyclic (as was proved in [a2], see also [a17]) and, on the other hand, any $2$-group the orders of whose Abelian (or finite) subgroups are bounded is itself finite (see [a7]).
, where $D ( 2 k )$ denotes a dihedral group of order $2 k$. The principal difference between odd and even exponents in the Burnside problem can be illustrated by pointing out that, on the one hand, for every odd $n \gg 1$ there are infinite $2$-generator groups of exponent $n$ all of whose proper subgroups are cyclic (as was proved in [a2], see also [a17]) and, on the other hand, any $2$-group the orders of whose Abelian (or finite) subgroups are bounded is itself finite (see [a7]).
In 1997, Ivanov and Ol'shanskii [a10] showed that the above description of finite subgroups in $B ( m , n )$ is complete (that is, every subgroup of $D ( 2 n_1 ) \times D ( 2 n_2 ) ^ { \text{l} }$ can actually be found in $B ( m , n )$) and obtained the following result: Let $G$ be a finite $2$-subgroup of $B ( m , n )$. Then the centralizer $C_{B ( m , n )} ( G )$ of $G$ in $B ( m , n )$ contains a subgroup $B$ isomorphic to a free Burnside group $B ( \infty , n )$ of infinite countable rank such that $G \cap B = \{ 1 \}$, whence $\langle G , B \rangle = G \times B$. (Since $B ( \infty , n )$ obviously contains subgroups isomorphic to both $D ( 2 n _ { 1 } )$ and $D ( 2 n _ { 2 } )$, an embedding of $D ( 2 n_1 ) \times D ( 2 n_2 ) ^ { \text{l} }$ in $B ( m , n )$ becomes trivial.) Among other results on subgroups of $B ( m , n )$ proven in [a10] are the following: The centralizer $C _ { B ( m , n ) } ( S )$ of a subgroup $S$ is infinite if and only if $S$ is a locally finite $2$-group. Any infinite locally finite subgroup $L$ is contained in a unique maximal locally finite subgroup while any finite $2$-subgroup is contained in continuously many pairwise non-isomorphic maximal locally finite subgroups. A complete description of infinite (maximal) locally finite subgroups of $B ( m , n )$ has also been obtained, in [a10].
References
| [a1] | S.I. Adian, "The Burnside problems and identities in groups" , Springer (1979) (In Russian) |
| [a2] | V.S. Atabekian, S.V. Ivanov, "Two remarks on groups of bounded exponent" , 2243-B87 , VINITI, Moscow (1987) ((This is kept in the Depot of VINITI, Moscow, and is available upon request)) |
| [a3] | W. Burnside, "An unsettled question in the theory of discontinuous groups" Quart. J. Pure Appl. Math. , 33 (1902) pp. 230–238 |
| [a4] | N. Gupta, "On groups in which every element has finite order" Amer. Math. Monthly , 96 (1989) pp. 297–308 |
| [a5] | M. Gromov, "Hyperbolic groups" S.M. Gersten (ed.) , Essays in Group Theory , Springer (1987) pp. 75–263 |
| [a6] | Ph. Hall, G. Higman, "On the $p$-length of $p$-soluble groups and reduction theorems for Burnside's problem" Proc. London Math. Soc. , 6 (1956) pp. 1–42 |
| [a7] | D. Held, "On abelian subgroups of an infinite $2$-group" Acta Sci. Math. (Szeged) , 27 (1966) pp. 97–98 |
| [a8] | M. Hall Jr., "Solution of the Burnside problem for exponent $6$" Proc. Nat. Acad. Sci. USA , 43 (1957) pp. 751–753 |
| [a9] | S.V. Ivanov, "The free Burnside groups of sufficiently large exponents" Internat. J. Algebra Comput. , 4 (1994) pp. 1–308 |
| [a10] | S.V. Ivanov, A.Yu. Ol'shanskii, "On finite and locally finite subgroups of free Burnside groups of large even exponents" J. Algebra , 195 (1997) pp. 241–284 |
| [a11] | A.I. Kostrikin, "On the Burnside problem" Math. USSR Izv. , 23 (1959) pp. 3–34 (In Russian) |
| [a12] | A.I. Kostrikin, "Around Burnside" , Nauka (1986) (In Russian) |
| [a13] | I.G. Lysenok, "Infinite Burnside groups of even period" Math. Ross. Izv. , 60 (1996) pp. 3–224 |
| [a14] | W. Magnus, "A connection between the Baker–Hausdorff formula and a problem of Burnside" Ann. Math. , 52 (1950) pp. 11–26 (Also: 57 (1953), 606) |
| [a15] | P.S. Novikov, S.I. Adian, "On infinite periodic groups I–III" Math. USSR Izv. , 32 (1968) pp. 212–244; 251–524; 709–731 |
| [a16] | A.Yu. Ol'shanskii, "On the Novikov–Adian theorem" Math. USSR Sb. , 118 (1982) pp. 203–235 (In Russian) |
| [a17] | A.Yu. Ol'shanskii, "Geometry of defining relations in groups" , Kluwer Acad. Publ. (1991) (In Russian) |
| [a18] | I.N. Sanov, "Solution of the Burnside problem for exponent $4$" Uch. Zapiski Leningrad State Univ. Ser. Mat. , 10 (1940) pp. 166–170 |
| [a19] | E.I. Zel'manov, "Solution of the restricted Burnside problem for groups of odd exponent" Math. USSR Izv. , 36 (1991) pp. 41–60 (In Russian) |
| [a20] | E.I. Zel'manov, "A solution of the restricted Burnside problem for $2$-groups" Math. USSR Sb. , 72 (1992) pp. 543–565 (In Russian) |
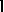 , where $D ( 2 k )$ denotes a dihedral group of order $2 k$. The principal difference between odd and even exponents in the Burnside problem can be illustrated by pointing out that, on the one hand, for every odd $n \gg 1$ there are infinite $2$-generator groups of exponent $n$ all of whose proper subgroups are cyclic (as was proved in [a2], see also [a17]) and, on the other hand, any $2$-group the orders of whose Abelian (or finite) subgroups are bounded is itself finite (see [a7]).
, where $D ( 2 k )$ denotes a dihedral group of order $2 k$. The principal difference between odd and even exponents in the Burnside problem can be illustrated by pointing out that, on the one hand, for every odd $n \gg 1$ there are infinite $2$-generator groups of exponent $n$ all of whose proper subgroups are cyclic (as was proved in [a2], see also [a17]) and, on the other hand, any $2$-group the orders of whose Abelian (or finite) subgroups are bounded is itself finite (see [a7]).