Difference between revisions of "Matrix variate distribution"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 65 formulas out of 68 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 68 formulas, 65 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A matrix random phenomenon is an observable phenomenon that can be represented in matrix form and that, under repeated observations, yields different outcomes which are not deterministically predictable. Instead, the outcomes obey certain conditions of statistical regularity. The set of descriptions of all possible outcomes that may occur on observing a matrix random phenomenon is the [[Sampling space|sampling space]] $\mathcal{S}$. A matrix event is a subset of $\mathcal{S}$. A measure of the degree of certainty with which a given matrix event will occur when observing a matrix random phenomenon can be found by defining a [[Probability|probability]] function on subsets of $\mathcal{S}$, assigning a [[Probability|probability]] to every matrix event. | ||
| − | + | A [[Matrix|matrix]] $X ( p \times n )$ consisting of $n p$ elements $x _ { 11 } ( \cdot ) , \ldots , x _ { p n } ( \cdot )$ which are real-valued functions defined on $\mathcal{S}$ is a real random matrix if the range $\mathbf{R} ^ { p \times n }$ of | |
| − | + | \begin{equation*} \left( \begin{array} { c c c } { x _ { 11 } ( . ) } & { \dots } & { x _ { 1 n } ( . ) } \\ { \vdots } & { \square } & { \vdots } \\ { x _ { p 1 } ( . ) } & { \dots } & { x _ { p n } (1) } \end{array} \right), \end{equation*} | |
| − | in | + | consists of Borel sets in the $n p$-dimensional real space and if for each [[Borel set|Borel set]] $B$ of real $n p$-tuples, arranged in a matrix, |
| − | + | \begin{equation*} \left( \begin{array} { c c c } { x _ { 11 } } & { \dots } & { x _ { 1 n} } \\ { \vdots } & { \square } & { \vdots } \\ { x _ { p 1 } } & { \dots } & { x _ { p n} } \end{array} \right), \end{equation*} | |
| − | + | in $\mathbf{R} ^ { p \times n }$, the set | |
| − | + | \begin{equation*} \left\{ s \in \mathcal{S} : \left( \begin{array} { c c c } { x _ { 11 } ( s _ { 11 } ) } & { \dots } & { x _ { 1 n } ( s _ { 1 n } ) } \\ { \vdots } & { \square } & { \vdots } \\ { x _ { p 1 } ( s _ { p 1 } ) } & { \dots } & { x _ { p n } ( s _ { p n } ) } \end{array} \right) \in B \right\} \end{equation*} | |
| − | + | is an event in $\mathcal{S}$. The probability density function of $X$ (cf. also [[Density of a probability distribution|Density of a probability distribution]]) is a scalar function $f _ { X } ( X )$ such that: | |
| − | + | i) $f _ { X } ( X ) \geq 0$; | |
| − | + | ii) $\int _ { X } f _ { X } ( X ) d X = 1$; and | |
| − | + | iii) $\mathsf{P} ( X \in A ) = \int _ { A } f _ { X } ( X ) d X$, where $A$ is a subset of the space of realizations of $X$. A scalar function $f _ { X , Y } ( X , Y )$ defines the joint (bi-matrix variate) probability density function of $X$ and $Y$ if | |
| − | + | a) $f _ { X , Y } ( X , Y ) \geq 0$; | |
| − | + | b) $\int _ { Y } \int_X f _ { X , Y } d X d Y = 1$; and | |
| − | + | c) $\mathsf{P} ( ( X , Y ) \in A ) = \int \int _ { A } f _ { X , Y } d X d Y$, where $A$ is a subset of the space of realizations of $( X , Y )$. | |
| − | + | The marginal probability density function of $X$ is defined by $f _ { X } ( X ) = \int _ { Y } f _ { X , Y } ( X , Y ) d Y$, and the conditional probability density function of $X$ given $Y$ is defined by | |
| − | + | \begin{equation*} f _ { X | Y } ( X | Y ) = \frac { f _ { X , Y } ( X , Y ) } { f _ { Y } ( Y ) } ,\; f _ { Y } ( Y ) > 0, \end{equation*} | |
| − | + | where $f _ { Y } ( Y )$ is the marginal probability density function of $Y$. | |
| − | + | Two random matrices $X ( p \times n )$ and $Y ( r \times s )$ are independently distributed if and only if | |
| − | + | \begin{equation*} f _ { X , Y } ( X , Y ) = f _ { X } ( X ) f _ { Y } ( Y ), \end{equation*} | |
| − | + | where $f _ { X } ( X )$ and $f _ { Y } ( Y )$ are the marginal densities of $X$ and $Y$, respectively. | |
| − | + | The characteristic function of the random matrix $X ( p \times n )$ is defined as | |
| − | + | \begin{equation*} \phi _ { X } ( Z ) = \int _ { X } \operatorname { etr } ( i Z X ^ { \prime } ) f _ { X } ( X ) d X \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | where $Z ( p \times n )$ is a real arbitrary matrix and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120150/m12015049.png"/> is the exponential trace function $\operatorname { etr } ( A ) = \operatorname { exp } ( \operatorname { tr } ( A ) )$. |
| + | |||
| + | For the random matrix $X ( p \times n ) = ( X _ { ij } )$, the mean matrix is given by $\mathsf{E} ( X ) = ( \mathsf{E} ( X _ { ij } ) )$. The $( p n \times r s )$ covariance matrix of the random matrices $X ( p \times n )$ and $Y ( r \times s )$ is defined by | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120150/m12015056.png"/></td> </tr></table> | ||
==Examples of matrix variate distributions.== | ==Examples of matrix variate distributions.== | ||
The matrix variate normal distribution | The matrix variate normal distribution | ||
| − | + | \begin{equation*} \frac { 1 } { ( 2 \pi ) ^ { n p / 2 } | \Sigma | ^ { n / 2 } | \Psi | ^ { p / 2 } } \times \end{equation*} | |
| − | + | \begin{equation*} \times \operatorname { etr } \left\{ - \frac { 1 } { 2 } \Sigma ^ { - 1 } ( X - M ) \Psi ^ { - 1 } ( X - M ) ^ { \prime } \right\} , X \in \mathbf{R} ^ { p \times n } , M \in \mathbf{R} ^ { p \times n } , \Sigma > 0 , \Psi > 0. \end{equation*} | |
The [[Wishart distribution|Wishart distribution]] | The [[Wishart distribution|Wishart distribution]] | ||
| − | + | \begin{equation*} \frac { 1 } { 2 ^ { n p / 2 } \Gamma _ { p } ( n / 2 ) | \Sigma | ^ { n / 2 } } | S | ^ { ( n - p - 1 ) / 2 } \operatorname { etr } \left( - \frac { 1 } { 2 } \Sigma ^ { - 1 } S \right), \end{equation*} | |
| − | + | \begin{equation*} S > 0 , n \geq p. \end{equation*} | |
| − | The matrix variate | + | The matrix variate $t$-distribution |
| − | + | \begin{equation*} \frac { \Gamma _ { p } \left[ \frac { \langle n + m + p - 1 \rangle} { 2 } \right] } { \pi ^ { m p / 2 } \Gamma _ { p } ( ( n + p - 1 ) / 2 ) } | \Sigma | ^ { - m / 2 } | \Omega | ^ { - p / 2 } \times \end{equation*} | |
| − | + | \begin{equation*} \times \left| I _ { p } + \Sigma ^ { - 1 } ( X - M ) \Omega ^ { - 1 } ( X - M ) ^ { \prime } \right| ^ { - ( n + m + p - 1 ) / 2 } , X \in {\bf R} ^ { p \times n } , M \in {\bf R} ^ { p \times n } , \Sigma > 0 , \Omega > 0. \end{equation*} | |
The matrix variate beta-type-I distribution | The matrix variate beta-type-I distribution | ||
| − | + | \begin{equation*} \frac { 1 } { \beta _ { p } ( a , b ) } | U | ^ { a - ( p + 1 ) / 2 } | I _ { p } - U | ^ { b - ( p + 1 ) / 2 }, \end{equation*} | |
| − | + | \begin{equation*} 0 < U < I _ { p } , a > \frac { 1 } { 2 } ( p - 1 ) , b > \frac { 1 } { 2 } ( p - 1 ). \end{equation*} | |
The matrix variate beta-type-II distribution | The matrix variate beta-type-II distribution | ||
| − | + | \begin{equation*} \frac { 1 } { \beta _ { p } ( a , b ) } | V | ^ { a - ( p + 1 ) / 2 } | I _ { p } + V | ^ { - ( a + b ) }, \end{equation*} | |
| − | + | \begin{equation*} V > 0 , a > \frac { 1 } { 2 } ( p - 1 ) , b > \frac { 1 } { 2 } ( p - 1 ). \end{equation*} | |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> P. Bougerol, J. Lacroix, "Products of random matrices with applications to Schrödinger operators" , Birkhäuser (1985)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> M. Carmeli, "Statistical theory and random matrices" , M. Dekker (1983)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> "Random matrices and their applications" J.E. Cohen (ed.) H. Kesten (ed.) C.M. Newman (ed.) , Amer. Math. Soc. (1986)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> A.K. Gupta, T. Varga, "Elliptically contoured models in statistics" , Kluwer Acad. Publ. (1993)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> A.K. Gupta, V.L. Girko, "Multidimensional statistical analysis and theory of random matrices" , VSP (1996)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> M.L. Mehta, "Random matrices" , Acad. Press (1991) (Edition: Second)</td></tr></table> |
Revision as of 16:58, 1 July 2020
A matrix random phenomenon is an observable phenomenon that can be represented in matrix form and that, under repeated observations, yields different outcomes which are not deterministically predictable. Instead, the outcomes obey certain conditions of statistical regularity. The set of descriptions of all possible outcomes that may occur on observing a matrix random phenomenon is the sampling space $\mathcal{S}$. A matrix event is a subset of $\mathcal{S}$. A measure of the degree of certainty with which a given matrix event will occur when observing a matrix random phenomenon can be found by defining a probability function on subsets of $\mathcal{S}$, assigning a probability to every matrix event.
A matrix $X ( p \times n )$ consisting of $n p$ elements $x _ { 11 } ( \cdot ) , \ldots , x _ { p n } ( \cdot )$ which are real-valued functions defined on $\mathcal{S}$ is a real random matrix if the range $\mathbf{R} ^ { p \times n }$ of
\begin{equation*} \left( \begin{array} { c c c } { x _ { 11 } ( . ) } & { \dots } & { x _ { 1 n } ( . ) } \\ { \vdots } & { \square } & { \vdots } \\ { x _ { p 1 } ( . ) } & { \dots } & { x _ { p n } (1) } \end{array} \right), \end{equation*}
consists of Borel sets in the $n p$-dimensional real space and if for each Borel set $B$ of real $n p$-tuples, arranged in a matrix,
\begin{equation*} \left( \begin{array} { c c c } { x _ { 11 } } & { \dots } & { x _ { 1 n} } \\ { \vdots } & { \square } & { \vdots } \\ { x _ { p 1 } } & { \dots } & { x _ { p n} } \end{array} \right), \end{equation*}
in $\mathbf{R} ^ { p \times n }$, the set
\begin{equation*} \left\{ s \in \mathcal{S} : \left( \begin{array} { c c c } { x _ { 11 } ( s _ { 11 } ) } & { \dots } & { x _ { 1 n } ( s _ { 1 n } ) } \\ { \vdots } & { \square } & { \vdots } \\ { x _ { p 1 } ( s _ { p 1 } ) } & { \dots } & { x _ { p n } ( s _ { p n } ) } \end{array} \right) \in B \right\} \end{equation*}
is an event in $\mathcal{S}$. The probability density function of $X$ (cf. also Density of a probability distribution) is a scalar function $f _ { X } ( X )$ such that:
i) $f _ { X } ( X ) \geq 0$;
ii) $\int _ { X } f _ { X } ( X ) d X = 1$; and
iii) $\mathsf{P} ( X \in A ) = \int _ { A } f _ { X } ( X ) d X$, where $A$ is a subset of the space of realizations of $X$. A scalar function $f _ { X , Y } ( X , Y )$ defines the joint (bi-matrix variate) probability density function of $X$ and $Y$ if
a) $f _ { X , Y } ( X , Y ) \geq 0$;
b) $\int _ { Y } \int_X f _ { X , Y } d X d Y = 1$; and
c) $\mathsf{P} ( ( X , Y ) \in A ) = \int \int _ { A } f _ { X , Y } d X d Y$, where $A$ is a subset of the space of realizations of $( X , Y )$.
The marginal probability density function of $X$ is defined by $f _ { X } ( X ) = \int _ { Y } f _ { X , Y } ( X , Y ) d Y$, and the conditional probability density function of $X$ given $Y$ is defined by
\begin{equation*} f _ { X | Y } ( X | Y ) = \frac { f _ { X , Y } ( X , Y ) } { f _ { Y } ( Y ) } ,\; f _ { Y } ( Y ) > 0, \end{equation*}
where $f _ { Y } ( Y )$ is the marginal probability density function of $Y$.
Two random matrices $X ( p \times n )$ and $Y ( r \times s )$ are independently distributed if and only if
\begin{equation*} f _ { X , Y } ( X , Y ) = f _ { X } ( X ) f _ { Y } ( Y ), \end{equation*}
where $f _ { X } ( X )$ and $f _ { Y } ( Y )$ are the marginal densities of $X$ and $Y$, respectively.
The characteristic function of the random matrix $X ( p \times n )$ is defined as
\begin{equation*} \phi _ { X } ( Z ) = \int _ { X } \operatorname { etr } ( i Z X ^ { \prime } ) f _ { X } ( X ) d X \end{equation*}
where $Z ( p \times n )$ is a real arbitrary matrix and 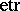 is the exponential trace function $\operatorname { etr } ( A ) = \operatorname { exp } ( \operatorname { tr } ( A ) )$.
is the exponential trace function $\operatorname { etr } ( A ) = \operatorname { exp } ( \operatorname { tr } ( A ) )$.
For the random matrix $X ( p \times n ) = ( X _ { ij } )$, the mean matrix is given by $\mathsf{E} ( X ) = ( \mathsf{E} ( X _ { ij } ) )$. The $( p n \times r s )$ covariance matrix of the random matrices $X ( p \times n )$ and $Y ( r \times s )$ is defined by
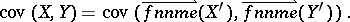 |
Examples of matrix variate distributions.
The matrix variate normal distribution
\begin{equation*} \frac { 1 } { ( 2 \pi ) ^ { n p / 2 } | \Sigma | ^ { n / 2 } | \Psi | ^ { p / 2 } } \times \end{equation*}
\begin{equation*} \times \operatorname { etr } \left\{ - \frac { 1 } { 2 } \Sigma ^ { - 1 } ( X - M ) \Psi ^ { - 1 } ( X - M ) ^ { \prime } \right\} , X \in \mathbf{R} ^ { p \times n } , M \in \mathbf{R} ^ { p \times n } , \Sigma > 0 , \Psi > 0. \end{equation*}
\begin{equation*} \frac { 1 } { 2 ^ { n p / 2 } \Gamma _ { p } ( n / 2 ) | \Sigma | ^ { n / 2 } } | S | ^ { ( n - p - 1 ) / 2 } \operatorname { etr } \left( - \frac { 1 } { 2 } \Sigma ^ { - 1 } S \right), \end{equation*}
\begin{equation*} S > 0 , n \geq p. \end{equation*}
The matrix variate $t$-distribution
\begin{equation*} \frac { \Gamma _ { p } \left[ \frac { \langle n + m + p - 1 \rangle} { 2 } \right] } { \pi ^ { m p / 2 } \Gamma _ { p } ( ( n + p - 1 ) / 2 ) } | \Sigma | ^ { - m / 2 } | \Omega | ^ { - p / 2 } \times \end{equation*}
\begin{equation*} \times \left| I _ { p } + \Sigma ^ { - 1 } ( X - M ) \Omega ^ { - 1 } ( X - M ) ^ { \prime } \right| ^ { - ( n + m + p - 1 ) / 2 } , X \in {\bf R} ^ { p \times n } , M \in {\bf R} ^ { p \times n } , \Sigma > 0 , \Omega > 0. \end{equation*}
The matrix variate beta-type-I distribution
\begin{equation*} \frac { 1 } { \beta _ { p } ( a , b ) } | U | ^ { a - ( p + 1 ) / 2 } | I _ { p } - U | ^ { b - ( p + 1 ) / 2 }, \end{equation*}
\begin{equation*} 0 < U < I _ { p } , a > \frac { 1 } { 2 } ( p - 1 ) , b > \frac { 1 } { 2 } ( p - 1 ). \end{equation*}
The matrix variate beta-type-II distribution
\begin{equation*} \frac { 1 } { \beta _ { p } ( a , b ) } | V | ^ { a - ( p + 1 ) / 2 } | I _ { p } + V | ^ { - ( a + b ) }, \end{equation*}
\begin{equation*} V > 0 , a > \frac { 1 } { 2 } ( p - 1 ) , b > \frac { 1 } { 2 } ( p - 1 ). \end{equation*}
References
| [a1] | P. Bougerol, J. Lacroix, "Products of random matrices with applications to Schrödinger operators" , Birkhäuser (1985) |
| [a2] | M. Carmeli, "Statistical theory and random matrices" , M. Dekker (1983) |
| [a3] | "Random matrices and their applications" J.E. Cohen (ed.) H. Kesten (ed.) C.M. Newman (ed.) , Amer. Math. Soc. (1986) |
| [a4] | A.K. Gupta, T. Varga, "Elliptically contoured models in statistics" , Kluwer Acad. Publ. (1993) |
| [a5] | A.K. Gupta, V.L. Girko, "Multidimensional statistical analysis and theory of random matrices" , VSP (1996) |
| [a6] | M.L. Mehta, "Random matrices" , Acad. Press (1991) (Edition: Second) |
Matrix variate distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_variate_distribution&oldid=50270