Difference between revisions of "Spencer cohomology"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 59 formulas out of 63 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 63 formulas, 59 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
The [[De Rham cohomology|de Rham cohomology]] and Dolbeault cohomology (cf. [[Duality in complex analysis|Duality in complex analysis]]) can be viewed as cohomologies with coefficients in the [[Sheaf|sheaf]] of locally constant, respectively harmonic, functions. Spencer cohomology is a generalization of these two cohomologies for the case of the solution sheaf of an arbitrary [[Linear differential operator|linear differential operator]]. | The [[De Rham cohomology|de Rham cohomology]] and Dolbeault cohomology (cf. [[Duality in complex analysis|Duality in complex analysis]]) can be viewed as cohomologies with coefficients in the [[Sheaf|sheaf]] of locally constant, respectively harmonic, functions. Spencer cohomology is a generalization of these two cohomologies for the case of the solution sheaf of an arbitrary [[Linear differential operator|linear differential operator]]. | ||
| − | Namely, let | + | Namely, let $\alpha : E ( \alpha ) \rightarrow M$ and $\beta : E ( \beta ) \rightarrow M$ be smooth vector bundles (cf. also [[Vector bundle|Vector bundle]]) and let $D : \Gamma ( \alpha ) \rightarrow \Gamma ( \beta )$ be a linear differential operator acting from the module $\Gamma ( \alpha )$ of smooth sections of $\alpha$ to the module $\Gamma ( \beta )$. Denote by ${\frak G} _ { D }$ the sheaf of solutions of $D a = 0$. To find the cohomology of $M$ with coefficients in ${\frak G} _ { D }$ one needs a [[Resolvent|resolvent]] of the sheaf. |
Spencer cohomology appears as a result of constructing a resolvent by a locally exact complex of differential operators | Spencer cohomology appears as a result of constructing a resolvent by a locally exact complex of differential operators | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130480/s13048011.png"/></td> </tr></table> |
| − | where | + | where $\alpha = \alpha _ { 0 }$, $\alpha _ { 1 } = \beta$, $D = D _ { 0 }$. The condition that the complex be locally exact is too strong, and therefore D. Spencer proposed the weaker condition that the complex should be "formally exact" . In this setting, there exists for a formally integrable differential operator $D$ a canonical construction ([[#References|[a5]]], [[#References|[a6]]], [[#References|[a1]]]) of a complex, called the second (or sophisticated) Spencer complex. In this complex, |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130480/s13048016.png"/></td> </tr></table> |
| − | the vector bundles | + | the vector bundles $C _ { k }$ have the form $C _ { k } = \Lambda ^ { k } T ^ { * } M \otimes R _ { m } / \delta ( \Lambda ^ { k - 1 } T ^ { * } M \otimes g _ { m + 1 } )$, where $R _ { m } \subset J ^ { m } ( \alpha )$ are prolongations of the differential equation corresponding to $D$ (cf. also [[Prolongation of solutions of differential equations|Prolongation of solutions of differential equations]]) and $g _ { m }$ are the symbols of these prolongations (cf. also [[Symbol of an operator|Symbol of an operator]]). The differential operators $D _ { k }$ are first-order partial differential operators whose symbols are induced by the exterior multiplication. |
| − | The | + | The $\delta$-Poincaré lemma [[#References|[a6]]] shows that the [[Cohomology|cohomology]] of the complex does not depend on $m$ when $m$ is large enough. The stable cohomology $H _ { S } ^ { * } ( D )$ is called the Spencer cohomology of the differential operator $D$. |
| − | In general, the second Spencer complex does not produce a resolvent of | + | In general, the second Spencer complex does not produce a resolvent of ${\frak G} _ { D }$; however, it does in certain special cases, e.g. when $D$ is analytical operator [[#References|[a6]]]. |
| − | Almost-all cohomologies encountered in applications are of Spencer type. For example, de Rham cohomology corresponds to the differential | + | Almost-all cohomologies encountered in applications are of Spencer type. For example, de Rham cohomology corresponds to the differential $D = d : C ^ { \infty } ( M ) \rightarrow \Omega ^ { 1 } ( M )$, and the Dolbeault cohomology corresponds to the Cauchy–Riemann $\overline { \partial }$-operator $\overline { \partial } : \Omega ^ { p , 0 } ( M ) \rightarrow \Omega ^ { p , 1 } ( M )$. If $D$ is a determined operator such that not all covectors are characteristic, then $H _ { S } ^ { 0 } ( D ) =\operatorname{ ker} D$, $H _ { S } ^ { 1 } ( D ) = \text { coker } D$ and $H _ { S } ^ { i } ( D ) = 0$ for $i \geq 2$. In general, $H _ { S } ^ { 0 } ( D ) =\operatorname{ ker} D$ for each formally integrable operators $D$. |
In the case of Lie equations and corresponding geometrical structures (see [[#References|[a2]]]), the first Spencer cohomology gives an estimate of the set of deformations of the structure. | In the case of Lie equations and corresponding geometrical structures (see [[#References|[a2]]]), the first Spencer cohomology gives an estimate of the set of deformations of the structure. | ||
| − | If | + | If $D$ is an elliptic partial differential operator (cf. [[Elliptic partial differential equation|Elliptic partial differential equation]]) and $M$ is a compact [[Manifold|manifold]], then $\operatorname { dim} H _ { S } ^ { i } ( D ) < \infty$ and the [[Euler characteristic|Euler characteristic]] $\chi ( D ) = \sum ( - 1 ) ^ { i } \operatorname { dim } H _ { S } ^ { i } ( D )$ of the Spencer complex is called the index of $D$ (cf. also [[Index formulas|Index formulas]]; [[Index theory|Index theory]]). For elliptic Lie equations the index can be expressed in terms of characteristic classes corresponding to the geometrical structure ([[#References|[a3]]]). |
| − | As is well-known, there are two main methods for calculating the de Rham cohomology: the Leray–Serre spectral sequence (cf. also [[Spectral sequence|Spectral sequence]]) and the theorem on coincidence of de Rham cohomology with invariant cohomology on homogeneous manifolds. These methods also apply to Spencer cohomology, provided the operator | + | As is well-known, there are two main methods for calculating the de Rham cohomology: the Leray–Serre spectral sequence (cf. also [[Spectral sequence|Spectral sequence]]) and the theorem on coincidence of de Rham cohomology with invariant cohomology on homogeneous manifolds. These methods also apply to Spencer cohomology, provided the operator $D$ satisfies certain extra conditions. |
| − | Thus, if the base manifold | + | Thus, if the base manifold $M$ is the total space of a smooth bundle $\pi : M \rightarrow B$ over a simply-connected manifold $B$ and if the fibres of $\pi$ are not characteristic for $D$, then there exists a spectral sequence $( E _ { r } ^ { p q } , d _ { r } ^ { p q } )$ converging to the Spencer cohomology $H _ { S } ^ { * } ( D )$; its second term is $E _ { 2 } ^ { p q } = H ^ { p } ( B ) \otimes H _ { S } ^ { q } ( D _ { \pi } )$, where $D _ { \pi }$ is the fibrewise differential operator corresponding to $D$ [[#References|[a4]]]. |
| − | If | + | If $M = G / G_0$ is a homogeneous manifold and the structure group $G$ is a compact connected [[Lie group|Lie group]] of symmetries of $D$, then [[#References|[a4]]] the Spencer cohomology $H _ { S } ^ { * } ( D )$ coincides with the cohomology of the $G$-invariant Spencer complex if the non-trivial characters of $( G , G _ { 0 } )$ are non-characteristic. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> H. Goldschmidt, "Existence theorems for analytic linear partial differential equations" ''Ann. Math.'' , '''86''' (1967) pp. 246–270</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. Kumpera, D. Spencer, "Lie equations" ''Ann. Math. Studies'' , '''73''' (1972)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> V. Lychagin, V. Rubtsov, "Topological indices of Spencer complexes that are associated with geometric structures" ''Math. Notes'' , '''45''' (1989) pp. 305–312</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> V. Lychagin, L. Zilbergleit, "Spencer cohomologies and symmetry groups" ''Acta Applic. Math.'' , '''41''' (1995) pp. 227–245</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> D.G. Quillen, "Formal properties of overdetermined systems of linear partial differential equations" ''Thesis Harvard Univ.'' (1964)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> D. Spencer, "Overdetermined systems of linear partial differential operators" ''Bull. Amer. Math. Soc.'' , '''75''' (1969) pp. 179–239</td></tr></table> |
Revision as of 16:57, 1 July 2020
The de Rham cohomology and Dolbeault cohomology (cf. Duality in complex analysis) can be viewed as cohomologies with coefficients in the sheaf of locally constant, respectively harmonic, functions. Spencer cohomology is a generalization of these two cohomologies for the case of the solution sheaf of an arbitrary linear differential operator.
Namely, let $\alpha : E ( \alpha ) \rightarrow M$ and $\beta : E ( \beta ) \rightarrow M$ be smooth vector bundles (cf. also Vector bundle) and let $D : \Gamma ( \alpha ) \rightarrow \Gamma ( \beta )$ be a linear differential operator acting from the module $\Gamma ( \alpha )$ of smooth sections of $\alpha$ to the module $\Gamma ( \beta )$. Denote by ${\frak G} _ { D }$ the sheaf of solutions of $D a = 0$. To find the cohomology of $M$ with coefficients in ${\frak G} _ { D }$ one needs a resolvent of the sheaf.
Spencer cohomology appears as a result of constructing a resolvent by a locally exact complex of differential operators
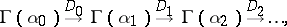 |
where $\alpha = \alpha _ { 0 }$, $\alpha _ { 1 } = \beta$, $D = D _ { 0 }$. The condition that the complex be locally exact is too strong, and therefore D. Spencer proposed the weaker condition that the complex should be "formally exact" . In this setting, there exists for a formally integrable differential operator $D$ a canonical construction ([a5], [a6], [a1]) of a complex, called the second (or sophisticated) Spencer complex. In this complex,
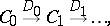 |
the vector bundles $C _ { k }$ have the form $C _ { k } = \Lambda ^ { k } T ^ { * } M \otimes R _ { m } / \delta ( \Lambda ^ { k - 1 } T ^ { * } M \otimes g _ { m + 1 } )$, where $R _ { m } \subset J ^ { m } ( \alpha )$ are prolongations of the differential equation corresponding to $D$ (cf. also Prolongation of solutions of differential equations) and $g _ { m }$ are the symbols of these prolongations (cf. also Symbol of an operator). The differential operators $D _ { k }$ are first-order partial differential operators whose symbols are induced by the exterior multiplication.
The $\delta$-Poincaré lemma [a6] shows that the cohomology of the complex does not depend on $m$ when $m$ is large enough. The stable cohomology $H _ { S } ^ { * } ( D )$ is called the Spencer cohomology of the differential operator $D$.
In general, the second Spencer complex does not produce a resolvent of ${\frak G} _ { D }$; however, it does in certain special cases, e.g. when $D$ is analytical operator [a6].
Almost-all cohomologies encountered in applications are of Spencer type. For example, de Rham cohomology corresponds to the differential $D = d : C ^ { \infty } ( M ) \rightarrow \Omega ^ { 1 } ( M )$, and the Dolbeault cohomology corresponds to the Cauchy–Riemann $\overline { \partial }$-operator $\overline { \partial } : \Omega ^ { p , 0 } ( M ) \rightarrow \Omega ^ { p , 1 } ( M )$. If $D$ is a determined operator such that not all covectors are characteristic, then $H _ { S } ^ { 0 } ( D ) =\operatorname{ ker} D$, $H _ { S } ^ { 1 } ( D ) = \text { coker } D$ and $H _ { S } ^ { i } ( D ) = 0$ for $i \geq 2$. In general, $H _ { S } ^ { 0 } ( D ) =\operatorname{ ker} D$ for each formally integrable operators $D$.
In the case of Lie equations and corresponding geometrical structures (see [a2]), the first Spencer cohomology gives an estimate of the set of deformations of the structure.
If $D$ is an elliptic partial differential operator (cf. Elliptic partial differential equation) and $M$ is a compact manifold, then $\operatorname { dim} H _ { S } ^ { i } ( D ) < \infty$ and the Euler characteristic $\chi ( D ) = \sum ( - 1 ) ^ { i } \operatorname { dim } H _ { S } ^ { i } ( D )$ of the Spencer complex is called the index of $D$ (cf. also Index formulas; Index theory). For elliptic Lie equations the index can be expressed in terms of characteristic classes corresponding to the geometrical structure ([a3]).
As is well-known, there are two main methods for calculating the de Rham cohomology: the Leray–Serre spectral sequence (cf. also Spectral sequence) and the theorem on coincidence of de Rham cohomology with invariant cohomology on homogeneous manifolds. These methods also apply to Spencer cohomology, provided the operator $D$ satisfies certain extra conditions.
Thus, if the base manifold $M$ is the total space of a smooth bundle $\pi : M \rightarrow B$ over a simply-connected manifold $B$ and if the fibres of $\pi$ are not characteristic for $D$, then there exists a spectral sequence $( E _ { r } ^ { p q } , d _ { r } ^ { p q } )$ converging to the Spencer cohomology $H _ { S } ^ { * } ( D )$; its second term is $E _ { 2 } ^ { p q } = H ^ { p } ( B ) \otimes H _ { S } ^ { q } ( D _ { \pi } )$, where $D _ { \pi }$ is the fibrewise differential operator corresponding to $D$ [a4].
If $M = G / G_0$ is a homogeneous manifold and the structure group $G$ is a compact connected Lie group of symmetries of $D$, then [a4] the Spencer cohomology $H _ { S } ^ { * } ( D )$ coincides with the cohomology of the $G$-invariant Spencer complex if the non-trivial characters of $( G , G _ { 0 } )$ are non-characteristic.
References
| [a1] | H. Goldschmidt, "Existence theorems for analytic linear partial differential equations" Ann. Math. , 86 (1967) pp. 246–270 |
| [a2] | A. Kumpera, D. Spencer, "Lie equations" Ann. Math. Studies , 73 (1972) |
| [a3] | V. Lychagin, V. Rubtsov, "Topological indices of Spencer complexes that are associated with geometric structures" Math. Notes , 45 (1989) pp. 305–312 |
| [a4] | V. Lychagin, L. Zilbergleit, "Spencer cohomologies and symmetry groups" Acta Applic. Math. , 41 (1995) pp. 227–245 |
| [a5] | D.G. Quillen, "Formal properties of overdetermined systems of linear partial differential equations" Thesis Harvard Univ. (1964) |
| [a6] | D. Spencer, "Overdetermined systems of linear partial differential operators" Bull. Amer. Math. Soc. , 75 (1969) pp. 179–239 |
Spencer cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spencer_cohomology&oldid=50201