Difference between revisions of "Almost-split sequence"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 73 formulas out of 74 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 74 formulas, 73 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''Auslander–Reiten sequence'' | ''Auslander–Reiten sequence'' | ||
Roughly speaking, almost-split sequences are minimal non-split short exact sequences. They were introduced by M. Auslander and I. Reiten in 1974–1975 and have become a central tool in the theory of representations of finite-dimensional algebras (cf. also [[Representation of an associative algebra|Representation of an associative algebra]]). | Roughly speaking, almost-split sequences are minimal non-split short exact sequences. They were introduced by M. Auslander and I. Reiten in 1974–1975 and have become a central tool in the theory of representations of finite-dimensional algebras (cf. also [[Representation of an associative algebra|Representation of an associative algebra]]). | ||
| − | Let | + | Let $R$ be an Artin algebra, i.e. $R$ is an associative ring with unity that is finitely generated as a module over its centre $Z ( R )$, which is a commutative Artinian ring. |
| − | Let | + | Let $C$ be an indecomposable non-projective finitely-generated left $R$-module. Then there exists a short exact sequence |
| − | + | \begin{equation} \tag{a1} 0 \rightarrow A \stackrel { f } { \rightarrow } B \stackrel { g } { \rightarrow } C \rightarrow 0 \end{equation} | |
| − | in | + | in $\square _ { R } \ \operatorname{Mod}$, the category of finitely-generated left $R$-modules, with the following properties: |
| − | i) | + | i) $A$ and $C$ are indecomposable; |
| − | ii) the sequence does not split, i.e. there is no section | + | ii) the sequence does not split, i.e. there is no section $s : C \rightarrow B$ of $g$ (a homomorphism such that $g s = \operatorname{id}$), or, equivalently, there is no retraction of $f$ (a homomorphism $r : B \rightarrow A$ such that $r f = \operatorname{id}$); |
| − | iii) given any | + | iii) given any $h : Z \rightarrow C$ with $Z$ indecomposable and $h$ not an isomorphism, there is a lift of $h$ to $B$ (i.e. a homomorphism $\tilde { h } : Z \rightarrow B$ in $\square _ { R } \ \operatorname{Mod}$ such that $g \tilde { h } = h$); |
| − | iv) given any | + | iv) given any $j : A \rightarrow X$ with $X$ indecomposable and $j$ not an isomorphism, there is a homomorphism $\tilde { j } : B \rightarrow X$ such that $\tilde { j } f = j$. |
| − | Note that if iii) (or, equivalently, iv)) were to hold for all | + | Note that if iii) (or, equivalently, iv)) were to hold for all $h$, not just those $h$ that are not isomorphisms, the sequence (a1) would be split, whence "almost split" . Moreover, a sequence (a1) with these properties is uniquely determined (up to isomorphism) by $C$, and also by $A$. This is the basic Auslander–Reiten theorem on almost-split sequences, [[#References|[a1]]], [[#References|[a8]]], [[#References|[a9]]], [[#References|[a10]]], [[#References|[a11]]]. |
| − | For convenience (things also work more generally), let now | + | For convenience (things also work more generally), let now $R$ be a finite-dimensional algebra over an algebraically closed field $k$. The category $\square _ { R } \ \operatorname{Mod}$ is a Krull–Schmidt category (Krull–Remak–Schmidt category), i.e. a $C \in \square _ { R } \operatorname{Mod}$ is indecomposable if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130220/a13022038.png"/>, the endomorphism ring of $C$, is a local ring and (hence) the decomposition of a module in $\square _ { R } \ \operatorname{Mod}$ into indecomposables is unique up to isomorphism. |
| − | Let | + | Let $C$ be an indecomposable and consider the contravariant functor $X \mapsto \square _ { R } \operatorname { Mod } ( X , C )$. The morphisms $g : X \rightarrow C$ that do not admit a section (i.e. an $s : C \rightarrow X$ such that $g s = \operatorname{id}$) form a vector subspace $E _ { C } ( X ) \subset \square _ { R } \operatorname { Mod } ( X , C )$. Let $S _ { C }$ be the quotient functor $S _ { C } = \operatorname { Mod } ( ? , C ) / E _ { C }$. Then, for an indecomposable $D$, $S _ { C } ( D ) = k$ if $D$ is isomorphic to $C$ and zero otherwise. So $S _ { C }$ is a simple functor. (All functors $\Box_R \text { Mod } ( ? , C )$, $E _ { C }$, $S _ { C }$ are viewed as $k$-functors, i.e. functors that take their values in the category of vector $k$-spaces.) If $C$ is indecomposable, then (the Auslander–Reiten theorem, [[#References|[a4]]], p.4) the simple functor $S _ { C }$ admits a minimal projective resolution of the form |
| − | + | \begin{equation*} 0 \rightarrow \square _ { R } \operatorname { Mod } ( ? , A ) \rightarrow \square _ { R } \operatorname { Mod } ( ? , B ) \rightarrow \end{equation*} | |
| − | + | \begin{equation*} \rightarrow \square _ { R } \text { Mod } ( ? , C ) \rightarrow S _ { C } \rightarrow 0. \end{equation*} | |
| − | If | + | If $C$ is projective, $A$ is zero, otherwise $A$ is indecomposable. |
| − | If | + | If $C$ is not projective, the sequence $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ is exact and is the almost-split sequence determined by $C$. |
This functorial definition is used in [[#References|[a5]]] in the somewhat more general setting of exact categories. | This functorial definition is used in [[#References|[a5]]] in the somewhat more general setting of exact categories. | ||
| Line 37: | Line 45: | ||
For a good introduction to the use of almost-split sequences, see [[#References|[a6]]]; see also [[#References|[a3]]], [[#References|[a5]]] for comprehensive treatments. See also [[Riedtmann classification|Riedtmann classification]] for the use of almost-split sequences and the Auslander–Reiten quiver in the classification of self-injective algebras. | For a good introduction to the use of almost-split sequences, see [[#References|[a6]]]; see also [[#References|[a3]]], [[#References|[a5]]] for comprehensive treatments. See also [[Riedtmann classification|Riedtmann classification]] for the use of almost-split sequences and the Auslander–Reiten quiver in the classification of self-injective algebras. | ||
| − | The Bautista–Brunner theorem says that if | + | The Bautista–Brunner theorem says that if $R$ is of finite representation type and $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ is an almost-split sequence, then $B$ has at most $4$ terms in its decomposition into indecomposables; also, if there are indeed $4$, then one of these is projective-injective. This can be generalized, [[#References|[a7]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> M. Auslander, I. Reiten, "Stable equivalence of dualizing $R$-varieties I" ''Adv. Math.'' , '''12''' (1974) pp. 306–366</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> M. Auslander, "The what, where, and why of almost split sequences" , ''Proc. ICM 1986, Berkeley'' , '''I''' , Amer. Math. Soc. (1987) pp. 338–345</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> M. Auslander, I. Reiten, S.O. Smalø, "Representation theory of Artin algebras" , Cambridge Univ. Press (1995)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> P. Gabriel, "Auslander–Reiten sequences and representation-finite algebras" V. Dlab (ed.) P. Gabriel (ed.) , ''Representation Theory I. Proc. Ottawa 1979 Conf.'' , Springer (1980) pp. 1–71</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> P. Gabriel, A.V. Roiter, "Representations of finite-dimensional algebras" , Springer (1997) pp. Sect. 9.3</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> I. Reiten, "The use of almost split sequences in the representation theory of Artin algebras" M. Auslander (ed.) E. Lluis (ed.) , ''Representation of Algebras. Proc. Puebla 1978 Workshop'' , Springer (1982) pp. 29–104</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> Shiping Liu, "Almost split sequenes for non-regular modules" ''Fundam. Math.'' , '''143''' (1993) pp. 183–190</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> M. Auslander, I. Reiten, "Representation theory of Artin algebras III" ''Commun. Algebra'' , '''3''' (1975) pp. 239–294</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> M. Auslander, I. Reiten, "Representation theory of Artin algebras IV" ''Commun. Algebra'' , '''5''' (1977) pp. 443–518</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> M. Auslander, I. Reiten, "Representation theory of Artin algebras V" ''Commun. Algebra'' , '''5''' (1977) pp. 519–554</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> M. Auslander, I. Reiten, "Representation theory of Artin algebras VI" ''Commun. Algebra'' , '''6''' (1978) pp. 257–300</td></tr></table> |
Revision as of 16:56, 1 July 2020
Auslander–Reiten sequence
Roughly speaking, almost-split sequences are minimal non-split short exact sequences. They were introduced by M. Auslander and I. Reiten in 1974–1975 and have become a central tool in the theory of representations of finite-dimensional algebras (cf. also Representation of an associative algebra).
Let $R$ be an Artin algebra, i.e. $R$ is an associative ring with unity that is finitely generated as a module over its centre $Z ( R )$, which is a commutative Artinian ring.
Let $C$ be an indecomposable non-projective finitely-generated left $R$-module. Then there exists a short exact sequence
\begin{equation} \tag{a1} 0 \rightarrow A \stackrel { f } { \rightarrow } B \stackrel { g } { \rightarrow } C \rightarrow 0 \end{equation}
in $\square _ { R } \ \operatorname{Mod}$, the category of finitely-generated left $R$-modules, with the following properties:
i) $A$ and $C$ are indecomposable;
ii) the sequence does not split, i.e. there is no section $s : C \rightarrow B$ of $g$ (a homomorphism such that $g s = \operatorname{id}$), or, equivalently, there is no retraction of $f$ (a homomorphism $r : B \rightarrow A$ such that $r f = \operatorname{id}$);
iii) given any $h : Z \rightarrow C$ with $Z$ indecomposable and $h$ not an isomorphism, there is a lift of $h$ to $B$ (i.e. a homomorphism $\tilde { h } : Z \rightarrow B$ in $\square _ { R } \ \operatorname{Mod}$ such that $g \tilde { h } = h$);
iv) given any $j : A \rightarrow X$ with $X$ indecomposable and $j$ not an isomorphism, there is a homomorphism $\tilde { j } : B \rightarrow X$ such that $\tilde { j } f = j$.
Note that if iii) (or, equivalently, iv)) were to hold for all $h$, not just those $h$ that are not isomorphisms, the sequence (a1) would be split, whence "almost split" . Moreover, a sequence (a1) with these properties is uniquely determined (up to isomorphism) by $C$, and also by $A$. This is the basic Auslander–Reiten theorem on almost-split sequences, [a1], [a8], [a9], [a10], [a11].
For convenience (things also work more generally), let now $R$ be a finite-dimensional algebra over an algebraically closed field $k$. The category $\square _ { R } \ \operatorname{Mod}$ is a Krull–Schmidt category (Krull–Remak–Schmidt category), i.e. a $C \in \square _ { R } \operatorname{Mod}$ is indecomposable if and only if 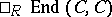 , the endomorphism ring of $C$, is a local ring and (hence) the decomposition of a module in $\square _ { R } \ \operatorname{Mod}$ into indecomposables is unique up to isomorphism.
, the endomorphism ring of $C$, is a local ring and (hence) the decomposition of a module in $\square _ { R } \ \operatorname{Mod}$ into indecomposables is unique up to isomorphism.
Let $C$ be an indecomposable and consider the contravariant functor $X \mapsto \square _ { R } \operatorname { Mod } ( X , C )$. The morphisms $g : X \rightarrow C$ that do not admit a section (i.e. an $s : C \rightarrow X$ such that $g s = \operatorname{id}$) form a vector subspace $E _ { C } ( X ) \subset \square _ { R } \operatorname { Mod } ( X , C )$. Let $S _ { C }$ be the quotient functor $S _ { C } = \operatorname { Mod } ( ? , C ) / E _ { C }$. Then, for an indecomposable $D$, $S _ { C } ( D ) = k$ if $D$ is isomorphic to $C$ and zero otherwise. So $S _ { C }$ is a simple functor. (All functors $\Box_R \text { Mod } ( ? , C )$, $E _ { C }$, $S _ { C }$ are viewed as $k$-functors, i.e. functors that take their values in the category of vector $k$-spaces.) If $C$ is indecomposable, then (the Auslander–Reiten theorem, [a4], p.4) the simple functor $S _ { C }$ admits a minimal projective resolution of the form
\begin{equation*} 0 \rightarrow \square _ { R } \operatorname { Mod } ( ? , A ) \rightarrow \square _ { R } \operatorname { Mod } ( ? , B ) \rightarrow \end{equation*}
\begin{equation*} \rightarrow \square _ { R } \text { Mod } ( ? , C ) \rightarrow S _ { C } \rightarrow 0. \end{equation*}
If $C$ is projective, $A$ is zero, otherwise $A$ is indecomposable.
If $C$ is not projective, the sequence $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ is exact and is the almost-split sequence determined by $C$.
This functorial definition is used in [a5] in the somewhat more general setting of exact categories.
For a good introduction to the use of almost-split sequences, see [a6]; see also [a3], [a5] for comprehensive treatments. See also Riedtmann classification for the use of almost-split sequences and the Auslander–Reiten quiver in the classification of self-injective algebras.
The Bautista–Brunner theorem says that if $R$ is of finite representation type and $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ is an almost-split sequence, then $B$ has at most $4$ terms in its decomposition into indecomposables; also, if there are indeed $4$, then one of these is projective-injective. This can be generalized, [a7].
References
| [a1] | M. Auslander, I. Reiten, "Stable equivalence of dualizing $R$-varieties I" Adv. Math. , 12 (1974) pp. 306–366 |
| [a2] | M. Auslander, "The what, where, and why of almost split sequences" , Proc. ICM 1986, Berkeley , I , Amer. Math. Soc. (1987) pp. 338–345 |
| [a3] | M. Auslander, I. Reiten, S.O. Smalø, "Representation theory of Artin algebras" , Cambridge Univ. Press (1995) |
| [a4] | P. Gabriel, "Auslander–Reiten sequences and representation-finite algebras" V. Dlab (ed.) P. Gabriel (ed.) , Representation Theory I. Proc. Ottawa 1979 Conf. , Springer (1980) pp. 1–71 |
| [a5] | P. Gabriel, A.V. Roiter, "Representations of finite-dimensional algebras" , Springer (1997) pp. Sect. 9.3 |
| [a6] | I. Reiten, "The use of almost split sequences in the representation theory of Artin algebras" M. Auslander (ed.) E. Lluis (ed.) , Representation of Algebras. Proc. Puebla 1978 Workshop , Springer (1982) pp. 29–104 |
| [a7] | Shiping Liu, "Almost split sequenes for non-regular modules" Fundam. Math. , 143 (1993) pp. 183–190 |
| [a8] | M. Auslander, I. Reiten, "Representation theory of Artin algebras III" Commun. Algebra , 3 (1975) pp. 239–294 |
| [a9] | M. Auslander, I. Reiten, "Representation theory of Artin algebras IV" Commun. Algebra , 5 (1977) pp. 443–518 |
| [a10] | M. Auslander, I. Reiten, "Representation theory of Artin algebras V" Commun. Algebra , 5 (1977) pp. 519–554 |
| [a11] | M. Auslander, I. Reiten, "Representation theory of Artin algebras VI" Commun. Algebra , 6 (1978) pp. 257–300 |
Almost-split sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Almost-split_sequence&oldid=50142