Difference between revisions of "Weyl correspondence"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 58 formulas out of 60 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 60 formulas, 58 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A mapping between a class of (generalized) functions on the phase space $\mathbf{R} ^ { 2 n }$ and the set of closed densely defined operators on the Hilbert space $L ^ { 2 } ( \mathbf{R} ^ { n } )$ [[#References|[a1]]] (cf. also [[Generalized function|Generalized function]]; [[Hilbert space|Hilbert space]]). It is defined as follows: Let $( q , p )$ be an arbitrary point of $\mathbf{R} ^ { 2 n }$ (called phase space) and let $\psi ( x )$ be an arbitrary vector on $L ^ { 2 } ( \mathbf{R} ^ { n } )$. For a point in $\mathbf{R} ^ { 2 n }$, the Grossmann–Royer operator $\Omega ( q , p )$ is defined as [[#References|[a2]]], [[#References|[a3]]]: | ||
| − | + | \begin{equation*} \Omega ( q , p ) \psi ( x ) = 2 ^ { n } \operatorname { exp } \{ 2 i p \cdot ( x - q ) \} \psi ( 2 q - x ). \end{equation*} | |
| + | |||
| + | Now, take a function $f ( q , p ) \in L ^ { 2 } ( \mathbf{R} ^ { 2 n } )$. The Weyl mapping $W$ is defined as [[#References|[a4]]], [[#References|[a5]]]: | ||
| + | |||
| + | \begin{equation*} W ( f ) = \frac { 1 } { 2 \pi } \int _ { R ^ { 2 n } } f ( q , p ) \Omega ( q , p ) d q d p. \end{equation*} | ||
The Weyl mapping defines the Weyl correspondence between functions and operators. It has the following properties: | The Weyl mapping defines the Weyl correspondence between functions and operators. It has the following properties: | ||
| Line 11: | Line 19: | ||
i) It is linear and one-to-one. | i) It is linear and one-to-one. | ||
| − | ii) If | + | ii) If $f$ is bounded, the operator $W ( f )$ is also bounded. |
| − | iii) If | + | iii) If $f$ is real, $W ( f )$ is self-adjoint (cf. also [[Self-adjoint operator|Self-adjoint operator]]). |
| − | iv) Let | + | iv) Let $f ( q , p ) , g ( q , p ) \in S ( {\bf R} ^ { 2 n } )$, the Schwartz space, and define the Weyl product as [[#References|[a6]]]: |
| − | + | \begin{equation*} ( f \times g ) ( q , p ) : = W ^ { - 1 } ( W ( f ) .W ( g ) ). \end{equation*} | |
| − | The Weyl product defines an algebra structure on | + | The Weyl product defines an algebra structure on $S ( \mathbf{R} ^ { 2 n } )$, which admits a closure $\mathcal{M} ( \mathbf{R} ^ { 2 n } )$ with the topology of the space of tempered distributions, $S ^ { \prime } ( \mathbf{R} ^ { 2 n } )$ (cf. also [[Generalized functions, space of|Generalized functions, space of]]). The algebra $\mathcal{M} ( \mathbf{R} ^ { 2 n } )$ includes the space $L ^ { 2 } ( \mathbf{R} ^ { 2 n } )$ and the Weyl mapping can be uniquely extended to $\mathcal{M} ( \mathbf{R} ^ { 2 n } )$. |
| − | v) Obviously, | + | v) Obviously, $W ( f \times g ) = W ( f ) . W ( g )$. |
| − | vi) If | + | vi) If $Q$ is the multiplication operator on $L ^ { 2 } ( \mathbf{R} ^ { n } )$ and $P = - i \overset{\rightharpoonup}{ \nabla }$, then $W ( q ^ { r } p ^ { s } ) = ( Q ^ { r } P ^ { s } )_S $, where $S$ denotes the symmetric product of $r$ factors $Q$ and $s$ factors $P$. |
| − | vii) For any positive trace-class operator | + | vii) For any positive trace-class operator $\rho$ on $L ^ { 2 } ( \mathbf{R} ^ { n } )$, there exists a signed measure $d\mu ( q , p )$ on $\mathbf{R} ^ { 2 n }$, such that for any $a , b \in \mathbf{R} ^ { n }$, |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120080/w12008040.png"/></td> </tr></table> |
| − | This measure has a Radon–Nikodým derivative (cf. also [[Radon–Nikodým theorem|Radon–Nikodým theorem]]) with respect to the [[Lebesgue measure|Lebesgue measure]], which is called the Wigner function associated to | + | This measure has a Radon–Nikodým derivative (cf. also [[Radon–Nikodým theorem|Radon–Nikodým theorem]]) with respect to the [[Lebesgue measure|Lebesgue measure]], which is called the Wigner function associated to $\rho$. |
| − | The Weyl correspondence is used by physicists to formulate quantum mechanics of non-relativistic systems without spin or other constraints on the flat phase space | + | The Weyl correspondence is used by physicists to formulate quantum mechanics of non-relativistic systems without spin or other constraints on the flat phase space $\mathbf{R} ^ { 2 n }$ [[#References|[a5]]]. |
| − | The Stratonovich–Weyl correspondence [[#References|[a4]]], [[#References|[a5]]], [[#References|[a7]]] or Stratonovich–Weyl mapping generalizes the Weyl mapping to other types of phase spaces. Choose a co-adjoint orbit | + | The Stratonovich–Weyl correspondence [[#References|[a4]]], [[#References|[a5]]], [[#References|[a7]]] or Stratonovich–Weyl mapping generalizes the Weyl mapping to other types of phase spaces. Choose a co-adjoint orbit $X$ of the representation group $\overline { G }$ of a certain [[Lie group|Lie group]] $G$ of symmetries of a given physical system as phase space. The [[Hilbert space|Hilbert space]] $\mathcal{H} ( X )$ used here supports a linear unitary irreducible representation of the group $\overline { G }$ associated to $X$. Then, a generalization of the Grossmann–Royer operator is needed, associating each point $u$ of the orbit $X$ with a self-adjoint operator $\Omega ( u )$. Then, for a suitable class of measurable functions $f ( u )$ on $X$, one defines: $W ( f ) = \int _ { X } f ( u ) \Omega ( u ) d \mu _ { X } ( u )$, where $d \mu _ { X } ( u )$ is a [[Measure|measure]] on $X$ that is invariant under the action of $\overline { G }$; such a measure is uniquely defined, up to a multiplicative constant. |
| − | The Weyl correspondence is a particular case of the Stratonovich–Weyl correspondence for which | + | The Weyl correspondence is a particular case of the Stratonovich–Weyl correspondence for which $G$ is the Heisenberg group, [[#References|[a1]]], [[#References|[a5]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> H. Weyl, "The theory of groups and quantum mechanics" , Dover (1931)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. Grossmann, "Parity operator and quantization of $\delta$ functions" ''Comm. Math. Phys.'' , '''48''' (1976) pp. 191</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> A. Royer, "Wigner function as the expectation value of a parity operator" ''Phys. Rev. A'' , '''15''' (1977) pp. 449</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> J.M. Gracia-Bondia, J.C. Varilly, "The Moyal representation of spin" ''Ann. Phys. (NY)'' , '''190''' (1989) pp. 107</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M. Gadella, "Moyal formulation of quantum mechanics" ''Fortschr. Phys.'' , '''43''' (1995) pp. 229</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> J.M. Gracia-Bondia, J.C. Varilly, "Algebras of distributions suitable for phase space quantum mechanics" ''J. Math. Phys.'' , '''29''' (1988) pp. 869</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> J.C. Varilly, "The Stratonovich–Weyl correspondence: a general approach to Wigner functions" ''BIBOS preprint 345 Univ. Bielefeld, Germany'' (1988)</td></tr></table> |
Revision as of 16:55, 1 July 2020
A mapping between a class of (generalized) functions on the phase space $\mathbf{R} ^ { 2 n }$ and the set of closed densely defined operators on the Hilbert space $L ^ { 2 } ( \mathbf{R} ^ { n } )$ [a1] (cf. also Generalized function; Hilbert space). It is defined as follows: Let $( q , p )$ be an arbitrary point of $\mathbf{R} ^ { 2 n }$ (called phase space) and let $\psi ( x )$ be an arbitrary vector on $L ^ { 2 } ( \mathbf{R} ^ { n } )$. For a point in $\mathbf{R} ^ { 2 n }$, the Grossmann–Royer operator $\Omega ( q , p )$ is defined as [a2], [a3]:
\begin{equation*} \Omega ( q , p ) \psi ( x ) = 2 ^ { n } \operatorname { exp } \{ 2 i p \cdot ( x - q ) \} \psi ( 2 q - x ). \end{equation*}
Now, take a function $f ( q , p ) \in L ^ { 2 } ( \mathbf{R} ^ { 2 n } )$. The Weyl mapping $W$ is defined as [a4], [a5]:
\begin{equation*} W ( f ) = \frac { 1 } { 2 \pi } \int _ { R ^ { 2 n } } f ( q , p ) \Omega ( q , p ) d q d p. \end{equation*}
The Weyl mapping defines the Weyl correspondence between functions and operators. It has the following properties:
i) It is linear and one-to-one.
ii) If $f$ is bounded, the operator $W ( f )$ is also bounded.
iii) If $f$ is real, $W ( f )$ is self-adjoint (cf. also Self-adjoint operator).
iv) Let $f ( q , p ) , g ( q , p ) \in S ( {\bf R} ^ { 2 n } )$, the Schwartz space, and define the Weyl product as [a6]:
\begin{equation*} ( f \times g ) ( q , p ) : = W ^ { - 1 } ( W ( f ) .W ( g ) ). \end{equation*}
The Weyl product defines an algebra structure on $S ( \mathbf{R} ^ { 2 n } )$, which admits a closure $\mathcal{M} ( \mathbf{R} ^ { 2 n } )$ with the topology of the space of tempered distributions, $S ^ { \prime } ( \mathbf{R} ^ { 2 n } )$ (cf. also Generalized functions, space of). The algebra $\mathcal{M} ( \mathbf{R} ^ { 2 n } )$ includes the space $L ^ { 2 } ( \mathbf{R} ^ { 2 n } )$ and the Weyl mapping can be uniquely extended to $\mathcal{M} ( \mathbf{R} ^ { 2 n } )$.
v) Obviously, $W ( f \times g ) = W ( f ) . W ( g )$.
vi) If $Q$ is the multiplication operator on $L ^ { 2 } ( \mathbf{R} ^ { n } )$ and $P = - i \overset{\rightharpoonup}{ \nabla }$, then $W ( q ^ { r } p ^ { s } ) = ( Q ^ { r } P ^ { s } )_S $, where $S$ denotes the symmetric product of $r$ factors $Q$ and $s$ factors $P$.
vii) For any positive trace-class operator $\rho$ on $L ^ { 2 } ( \mathbf{R} ^ { n } )$, there exists a signed measure $d\mu ( q , p )$ on $\mathbf{R} ^ { 2 n }$, such that for any $a , b \in \mathbf{R} ^ { n }$,
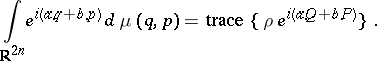 |
This measure has a Radon–Nikodým derivative (cf. also Radon–Nikodým theorem) with respect to the Lebesgue measure, which is called the Wigner function associated to $\rho$.
The Weyl correspondence is used by physicists to formulate quantum mechanics of non-relativistic systems without spin or other constraints on the flat phase space $\mathbf{R} ^ { 2 n }$ [a5].
The Stratonovich–Weyl correspondence [a4], [a5], [a7] or Stratonovich–Weyl mapping generalizes the Weyl mapping to other types of phase spaces. Choose a co-adjoint orbit $X$ of the representation group $\overline { G }$ of a certain Lie group $G$ of symmetries of a given physical system as phase space. The Hilbert space $\mathcal{H} ( X )$ used here supports a linear unitary irreducible representation of the group $\overline { G }$ associated to $X$. Then, a generalization of the Grossmann–Royer operator is needed, associating each point $u$ of the orbit $X$ with a self-adjoint operator $\Omega ( u )$. Then, for a suitable class of measurable functions $f ( u )$ on $X$, one defines: $W ( f ) = \int _ { X } f ( u ) \Omega ( u ) d \mu _ { X } ( u )$, where $d \mu _ { X } ( u )$ is a measure on $X$ that is invariant under the action of $\overline { G }$; such a measure is uniquely defined, up to a multiplicative constant.
The Weyl correspondence is a particular case of the Stratonovich–Weyl correspondence for which $G$ is the Heisenberg group, [a1], [a5].
References
| [a1] | H. Weyl, "The theory of groups and quantum mechanics" , Dover (1931) |
| [a2] | A. Grossmann, "Parity operator and quantization of $\delta$ functions" Comm. Math. Phys. , 48 (1976) pp. 191 |
| [a3] | A. Royer, "Wigner function as the expectation value of a parity operator" Phys. Rev. A , 15 (1977) pp. 449 |
| [a4] | J.M. Gracia-Bondia, J.C. Varilly, "The Moyal representation of spin" Ann. Phys. (NY) , 190 (1989) pp. 107 |
| [a5] | M. Gadella, "Moyal formulation of quantum mechanics" Fortschr. Phys. , 43 (1995) pp. 229 |
| [a6] | J.M. Gracia-Bondia, J.C. Varilly, "Algebras of distributions suitable for phase space quantum mechanics" J. Math. Phys. , 29 (1988) pp. 869 |
| [a7] | J.C. Varilly, "The Stratonovich–Weyl correspondence: a general approach to Wigner functions" BIBOS preprint 345 Univ. Bielefeld, Germany (1988) |
Weyl correspondence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_correspondence&oldid=50059