Difference between revisions of "Brouwer degree"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (AUTOMATIC EDIT (latexlist): Replaced 106 formulas out of 109 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 109 formulas, 106 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''topological degree'' | ''topological degree'' | ||
| − | A fundamental concept in [[Algebraic topology|algebraic topology]], [[Differential topology|differential topology]] and [[Mathematical analysis|mathematical analysis]]. It is rooted in the fundamental work of L. Kronecker [[#References|[a5]]] for systems of smooth real-valued functions | + | A fundamental concept in [[Algebraic topology|algebraic topology]], [[Differential topology|differential topology]] and [[Mathematical analysis|mathematical analysis]]. It is rooted in the fundamental work of L. Kronecker [[#References|[a5]]] for systems of smooth real-valued functions $f _ { 0 } , \dots , f _ { n }$ of $n$ real variables such that $0$ is a regular value for $f _ { 0 }$, $K : = f _ { 0 } ^ { - 1 } ( ] - \infty , 0 ] )$ is bounded and the $f_j$ do not vanish simultaneously on $\partial K$. Letting $f = ( f _ { 1 } , \dots , f _ { n } )$, Kronecker showed in 1869 that the number $\chi [ f _ { 0 } , \dots , f _ { n } ]$ defined (in modern notation) by the integral |
| − | + | \begin{equation*} \frac { 1 } { \operatorname{vol} S ^ { n - 1 } } \int _ { \partial K } f ^ { * } \omega, \end{equation*} | |
| − | where | + | where $\omega = \sum _ { j = 1 } ^ { n } ( - 1 ) ^ { j - 1 } \| x \| ^ { - n } x _ { j }\, d x _ { 1 } \wedge \ldots \wedge d x _ { j - 1 } \wedge d x _ { j + 1 } \wedge \ldots \wedge d x _ { n }$, is equal to $\sum _ { x \in f ^{ - 1} ( 0 ) \cap \partial K } \text { sign det } f ^ { \prime } ( x )$, when this sum makes sense, i.e. when the Jacobian of $f$ does not vanish on $f ^ { - 1 } ( 0 )$ (cf. also [[Jacobian|Jacobian]]). The special case when $n = 2$ and $\partial K$ is a closed simple curve was already considered by A. Cauchy in 1837 (the [[Winding number|winding number]]). After several interesting applications to differential equations and function theory by H. Poincaré in 1882–1886 and P.G. Bohl in 1904, in 1910–1912, L.E.J. Brouwer [[#References|[a2]]] and J. Hadamard [[#References|[a3]]] made this Kronecker integral a topological tool by extending it to continuous mappings $f$ and more general sets $K$. Hadamard refined Kronecker's analytical approach, but Brouwer created and used new simplicial techniques to define a (global) degree $d [ f , M , N ]$ for continuous mappings $f : M \rightarrow N$ between two oriented compact boundaryless connected manifolds of the same finite dimension. He used it to prove the theorems on invariance of dimension and invariance of domain (cf. also [[Brouwer theorem|Brouwer theorem]]). Kronecker's integral can be seen as a special case of the Brouwer degree $d [ f / \| f \| , \partial K , S ^ { n - 1 } ]$, or of the (local) Brouwer degree $\operatorname{deg}_{B}[f, \operatorname{int} K, 0]$, defined as follows (cf. also [[Degree of a mapping|Degree of a mapping]]). |
| − | If | + | If $\Omega \subset \mathbf{R} ^ { n }$ is open and bounded, the Brouwer degree $\operatorname{deg}_B [ f , \Omega , y ]$ of a continuous mapping $f : \overline { \Omega } \subset \mathbf{R} ^ { n } \rightarrow \mathbf{R} ^ { n }$ can be defined for each $y \notin f ( \partial \Omega )$ using an approximation scheme introduced by M. Nagumo [[#References|[a8]]] in 1950. The idea consists in defining it first for $f$ smooth and $y$ a regular value of $f$, through the formula |
| − | + | \begin{equation*} \sum _ { x \in f ^ { - 1 } ( y ) } \operatorname { sign } \operatorname { det } f ^ { \prime } ( x ), \end{equation*} | |
| − | and then to approximate the continuous function | + | and then to approximate the continuous function $f$ and the point $y$ above by a sequence of such functions and points for which this definition holds. This is possible by the Weierstrass approximation theorem (cf. [[Weierstrass theorem|Weierstrass theorem]]) and the [[Sard theorem|Sard theorem]]. The degrees of the approximations stabilize to a common value, denoted by $\operatorname{deg}_B [ f , \Omega , y ]$ and being an algebraic count of the number of counter-images of $y$ under $f$ in $\Omega$, which is stable for small perturbations of $f$ and $y$. A similar approach can be used to define $d [ f , M , N ]$ when $M$ and $N$ are oriented boundaryless differentiable manifolds. |
==Properties and axiomatic characterization.== | ==Properties and axiomatic characterization.== | ||
| − | The first basic property of the Brouwer degree is its additivity-excision: if | + | The first basic property of the Brouwer degree is its additivity-excision: if $\Omega _ { 1 } \subset \Omega$ and $\Omega _ { 2 } \subset \Omega$ are disjoint open subsets such that $y \notin f ( \overline { \Omega } \backslash ( \Omega _ { 1 } \cup \Omega _ { 2 } ) )$, then one has $\operatorname { deg } _ { B } [ f , \Omega , y ] = \operatorname { deg } _ { B } [ f , \Omega _ { 1 } , y ] + \operatorname { deg } _ { B } [ f , \Omega _ { 2 } , y ]$. |
| − | The second property is its homotopy invariance: let | + | The second property is its homotopy invariance: let $U \subset \mathbf{R} ^ { n } \times [ 0,1 ]$ be a bounded open set, $U _ { \lambda } = \{ x \in \mathbf{R} ^ { n } : ( x , \lambda ) \in U \}$, let $F : \overline { U } \rightarrow \mathbf{R} ^ { n }$ be continuous, and let $y \notin F ( \partial U )$; then $\operatorname { deg } _ { B } [ F ( ., \lambda ) , U _ { \lambda } , y ]$ is independent of $\lambda$. |
| − | It has been shown in the 1970s (see [[#References|[a9]]] for references) that the Brouwer degree can be uniquely characterized as the integer-valued function | + | It has been shown in the 1970s (see [[#References|[a9]]] for references) that the Brouwer degree can be uniquely characterized as the integer-valued function $\operatorname { deg } _ { B }$ on the set |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130260/b13026053.png"/></td> </tr></table> |
| − | by the additivity-excision and the homotopy invariance properties, together with the following direct consequence of the definition (the normalization property): if | + | by the additivity-excision and the homotopy invariance properties, together with the following direct consequence of the definition (the normalization property): if $y \in \Omega$, then $\operatorname{deg}_{B} [ l , \Omega , y ] = 1$. |
| − | The additivity-excision property implies the existence property: if | + | The additivity-excision property implies the existence property: if $\deg_B [ f , \Omega , y ] \neq 0$, then $y \in f ( \Omega )$. |
| − | Easy consequences of the homotopy invariance are the equalities | + | Easy consequences of the homotopy invariance are the equalities $\operatorname { deg } _ { B } [ f , \Omega , y ] = \operatorname { deg } _ { B } [ g , \Omega , y ]$ when $f = g$ on $\partial \Omega$, and $\operatorname { deg } _ { B } [ f , \Omega , y ] = \operatorname { deg } _ { B } [ f , \Omega , z ]$ when $y$ and $z$ belong to the same component $C_i$ of $\mathbf{R} ^ { n } \backslash f ( \partial \Omega )$ (with the common value written $\operatorname { deg } _ { B } [ f , \Omega , C _ { i } ]$). |
The existence and homotopy properties have many important applications in studying the existence and bifurcation of solutions of various types of equations. | The existence and homotopy properties have many important applications in studying the existence and bifurcation of solutions of various types of equations. | ||
==Product theorem.== | ==Product theorem.== | ||
| − | In 1934, J. Leray [[#References|[a6]]] proved a useful product theorem for the Brouwer degree: let | + | In 1934, J. Leray [[#References|[a6]]] proved a useful product theorem for the Brouwer degree: let $f : \overline { \Omega } \rightarrow \mathbf{R} ^ { n }$ and $g : \overline { \Delta } \rightarrow {\bf R} ^ { n }$, with $\Delta \supset f ( \overline { \Omega } )$, be continuous functions such that $y \notin g \circ f ( \partial \Omega )$. Denoting by $C_i$ the bounded components of $\Delta \backslash f ( \partial \Omega )$, one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130260/b13026073.png"/>, where only finitely many terms are different from zero. |
| − | This result has deep applications in topology, for example the Jordan separation theorem: for homeomorphic compact subsets | + | This result has deep applications in topology, for example the Jordan separation theorem: for homeomorphic compact subsets $K _ { 1 }$ and $K _ { 2 }$ of ${\bf R} ^ { n }$, the sets $\mathbf{R} ^ { n } \backslash K _ { 1 }$ and ${\bf R} ^ { n } \backslash K _ { 2 }$ have the same number of connected components. |
==Fixed-point theorems.== | ==Fixed-point theorems.== | ||
| − | An easy consequence of the Brouwer degree is the following Knaster–Kuratowski–Mazurkiewicz fixed-point theorem, first stated and proved in 1929 [[#References|[a4]]]: let | + | An easy consequence of the Brouwer degree is the following Knaster–Kuratowski–Mazurkiewicz fixed-point theorem, first stated and proved in 1929 [[#References|[a4]]]: let $B [ R ] \subset \mathbf{R} ^ { n }$ be the closed ball of centre $0$ and radius $R$ and let $g : B [ R ] \rightarrow \mathbf{R} ^ { n }$ be a continuous function such that $g ( \partial B [ R ] ) \subset B[R]$. Then there is at least one $x \in B [ R ]$ such that $g ( x ) = x$. |
| − | The special case where | + | The special case where $g : B [ R ] \rightarrow B [ R ]$ is the Brouwer fixed-point theorem [[#References|[a2]]], which has many different and useful equivalent forms. |
==Degree of symmetric mappings.== | ==Degree of symmetric mappings.== | ||
| − | Useful computational results hold under symmetry assumptions. The oldest one, which corresponds to | + | Useful computational results hold under symmetry assumptions. The oldest one, which corresponds to $\mathbf{Z}_{2}$-symmetry, was conjectured by S.M. Ulam and proved by K. Borsuk in 1933 [[#References|[a1]]]: let $\Omega$ be a bounded open symmetric neighbourhood of the origin in ${\bf R} ^ { n }$ and let $f : \overline { \Omega } \rightarrow \mathbf{R} ^ { n }$ be a continuous odd function such that $0 \notin f ( \partial \Omega )$; then $\text{deg}_B[ f , \Omega , 0 ]$ is odd. |
| − | This result and its more recent | + | This result and its more recent $S ^ { 1 }$-version are basic in critical point theory [[#References|[a7]]]. |
==Other approaches and extensions.== | ==Other approaches and extensions.== | ||
| − | The Brouwer degree is a very versatile concept which can be defined through techniques of algebraic topology, differential topology or algebraic geometry. For example, if | + | The Brouwer degree is a very versatile concept which can be defined through techniques of algebraic topology, differential topology or algebraic geometry. For example, if $f : S ^ { n } \rightarrow S ^ { n }$ is continuous and $f ^ { * } : H ^ { * } ( S ^ { n } ) \rightarrow H ^ { * } ( S ^ { n } )$ is the induced [[Homomorphism|homomorphism]] on the homology groups of $S ^ { n }$ over $\mathbf{Z}$ (cf. also [[Homology group|Homology group]]), then $H _ { n } ( S ^ { n } )$ is isomorphic to $\mathbf{Z}$ and hence $f _ { n } ^ { * }$ becomes multiplication by an integer, which is $d [ f , S ^ { n } , S ^ { n } ]$. If $\widetilde { f }$ is any continuous extension of $f$ to the closed unit ball $B ( 1 )$, then $d [ f , S ^ { n } , S ^ { n } ] = \operatorname { deg } _ { B } [ \tilde { f } , B ( 1 ) , 0 ]$. |
| − | In 1995, H. Brézis and L. Nirenberg [[#References|[a10]]], [[#References|[a11]]] defined a Brouwer degree for certain not necessarily continuous mappings | + | In 1995, H. Brézis and L. Nirenberg [[#References|[a10]]], [[#References|[a11]]] defined a Brouwer degree for certain not necessarily continuous mappings $f$ belonging to a Sobolev or other function space. |
Extensions of the Brouwer degree to various classes of mappings between infinite-dimensional spaces are also known. The most fundamental one is the Leray–Schauder degree, defined in 1934 for compact perturbations of the identity defined on the closure of a bounded open subset of a normed vector space (cf. also [[Degree of a mapping|Degree of a mapping]]). | Extensions of the Brouwer degree to various classes of mappings between infinite-dimensional spaces are also known. The most fundamental one is the Leray–Schauder degree, defined in 1934 for compact perturbations of the identity defined on the closure of a bounded open subset of a normed vector space (cf. also [[Degree of a mapping|Degree of a mapping]]). | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> K. Borsuk, "Drei Sätze über die $n$-dimensionale euklidische Sphäre" ''Fundam. Math.'' , '''21''' (1933) pp. 177–190</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> L.E.J. Brouwer, "Ueber Abbildungen von Mannigfaltigkeiten" ''Math. Ann.'' , '''71''' (1912) pp. 97–115</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J. Hadamard, "Sur quelques applications de l'indice de Kronecker" J. Tannery (ed.) , ''Introduction à la théorie des fonctions d'une variable'' , '''2''' , Hermann (1910) pp. 875–915</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> B. Knaster, C. Kuratowski, S. Mazurkiewicz, "Ein Beweis des Fixpunktsatzes für $n$-dimensionale Simplexe" ''Fundam. Math.'' , '''14''' (1929) pp. 132–137</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> L. Kronecker, "Ueber Systeme von Funktionen mehrerer Variabeln" ''Monatsber. Berlin Akad.'' (1869) pp. 159–193; 688–698 {{MR|}} {{ZBL|02.0203.02}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> J. Leray, "Topologie des espaces abstraits de M. Banach" ''C.R. Acad. Sci. Paris'' , '''200''' (1935) pp. 1082–1084 {{MR|}} {{ZBL|0011.16402}} {{ZBL|61.0613.03}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> J. Mawhin, M. Willem, "Critical point theory and Hamiltonian systems" , Springer (1989) {{MR|0982267}} {{ZBL|0676.58017}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> M. Nagumo, "A theory of degree of mapping based on infinitesimal analysis" ''Amer. J. Math.'' , '''73''' (1951) pp. 485–496 {{MR|0042696}} {{ZBL|0043.17802}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> E. Zeidler, "Nonlinear functional analysis and its applications" , '''I''' , Springer (1986) {{MR|0816732}} {{ZBL|0583.47050}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> H. Brézis, L. Nirenberg, "Degree theory and BMO" ''Selecta Math.'' , '''1''' (1995) pp. 197–263 {{MR|1354598}} {{ZBL|0868.58017}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> H. Brézis, L. Nirenberg, "Degree theory and BMO" ''Selecta Math.'' , '''2''' (1996) pp. 1–60 {{MR|1422201}} {{ZBL|0868.58017}} </td></tr></table> |
Revision as of 15:31, 1 July 2020
topological degree
A fundamental concept in algebraic topology, differential topology and mathematical analysis. It is rooted in the fundamental work of L. Kronecker [a5] for systems of smooth real-valued functions $f _ { 0 } , \dots , f _ { n }$ of $n$ real variables such that $0$ is a regular value for $f _ { 0 }$, $K : = f _ { 0 } ^ { - 1 } ( ] - \infty , 0 ] )$ is bounded and the $f_j$ do not vanish simultaneously on $\partial K$. Letting $f = ( f _ { 1 } , \dots , f _ { n } )$, Kronecker showed in 1869 that the number $\chi [ f _ { 0 } , \dots , f _ { n } ]$ defined (in modern notation) by the integral
\begin{equation*} \frac { 1 } { \operatorname{vol} S ^ { n - 1 } } \int _ { \partial K } f ^ { * } \omega, \end{equation*}
where $\omega = \sum _ { j = 1 } ^ { n } ( - 1 ) ^ { j - 1 } \| x \| ^ { - n } x _ { j }\, d x _ { 1 } \wedge \ldots \wedge d x _ { j - 1 } \wedge d x _ { j + 1 } \wedge \ldots \wedge d x _ { n }$, is equal to $\sum _ { x \in f ^{ - 1} ( 0 ) \cap \partial K } \text { sign det } f ^ { \prime } ( x )$, when this sum makes sense, i.e. when the Jacobian of $f$ does not vanish on $f ^ { - 1 } ( 0 )$ (cf. also Jacobian). The special case when $n = 2$ and $\partial K$ is a closed simple curve was already considered by A. Cauchy in 1837 (the winding number). After several interesting applications to differential equations and function theory by H. Poincaré in 1882–1886 and P.G. Bohl in 1904, in 1910–1912, L.E.J. Brouwer [a2] and J. Hadamard [a3] made this Kronecker integral a topological tool by extending it to continuous mappings $f$ and more general sets $K$. Hadamard refined Kronecker's analytical approach, but Brouwer created and used new simplicial techniques to define a (global) degree $d [ f , M , N ]$ for continuous mappings $f : M \rightarrow N$ between two oriented compact boundaryless connected manifolds of the same finite dimension. He used it to prove the theorems on invariance of dimension and invariance of domain (cf. also Brouwer theorem). Kronecker's integral can be seen as a special case of the Brouwer degree $d [ f / \| f \| , \partial K , S ^ { n - 1 } ]$, or of the (local) Brouwer degree $\operatorname{deg}_{B}[f, \operatorname{int} K, 0]$, defined as follows (cf. also Degree of a mapping).
If $\Omega \subset \mathbf{R} ^ { n }$ is open and bounded, the Brouwer degree $\operatorname{deg}_B [ f , \Omega , y ]$ of a continuous mapping $f : \overline { \Omega } \subset \mathbf{R} ^ { n } \rightarrow \mathbf{R} ^ { n }$ can be defined for each $y \notin f ( \partial \Omega )$ using an approximation scheme introduced by M. Nagumo [a8] in 1950. The idea consists in defining it first for $f$ smooth and $y$ a regular value of $f$, through the formula
\begin{equation*} \sum _ { x \in f ^ { - 1 } ( y ) } \operatorname { sign } \operatorname { det } f ^ { \prime } ( x ), \end{equation*}
and then to approximate the continuous function $f$ and the point $y$ above by a sequence of such functions and points for which this definition holds. This is possible by the Weierstrass approximation theorem (cf. Weierstrass theorem) and the Sard theorem. The degrees of the approximations stabilize to a common value, denoted by $\operatorname{deg}_B [ f , \Omega , y ]$ and being an algebraic count of the number of counter-images of $y$ under $f$ in $\Omega$, which is stable for small perturbations of $f$ and $y$. A similar approach can be used to define $d [ f , M , N ]$ when $M$ and $N$ are oriented boundaryless differentiable manifolds.
Properties and axiomatic characterization.
The first basic property of the Brouwer degree is its additivity-excision: if $\Omega _ { 1 } \subset \Omega$ and $\Omega _ { 2 } \subset \Omega$ are disjoint open subsets such that $y \notin f ( \overline { \Omega } \backslash ( \Omega _ { 1 } \cup \Omega _ { 2 } ) )$, then one has $\operatorname { deg } _ { B } [ f , \Omega , y ] = \operatorname { deg } _ { B } [ f , \Omega _ { 1 } , y ] + \operatorname { deg } _ { B } [ f , \Omega _ { 2 } , y ]$.
The second property is its homotopy invariance: let $U \subset \mathbf{R} ^ { n } \times [ 0,1 ]$ be a bounded open set, $U _ { \lambda } = \{ x \in \mathbf{R} ^ { n } : ( x , \lambda ) \in U \}$, let $F : \overline { U } \rightarrow \mathbf{R} ^ { n }$ be continuous, and let $y \notin F ( \partial U )$; then $\operatorname { deg } _ { B } [ F ( ., \lambda ) , U _ { \lambda } , y ]$ is independent of $\lambda$.
It has been shown in the 1970s (see [a9] for references) that the Brouwer degree can be uniquely characterized as the integer-valued function $\operatorname { deg } _ { B }$ on the set
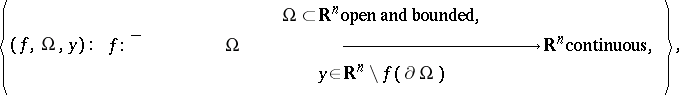 |
by the additivity-excision and the homotopy invariance properties, together with the following direct consequence of the definition (the normalization property): if $y \in \Omega$, then $\operatorname{deg}_{B} [ l , \Omega , y ] = 1$.
The additivity-excision property implies the existence property: if $\deg_B [ f , \Omega , y ] \neq 0$, then $y \in f ( \Omega )$.
Easy consequences of the homotopy invariance are the equalities $\operatorname { deg } _ { B } [ f , \Omega , y ] = \operatorname { deg } _ { B } [ g , \Omega , y ]$ when $f = g$ on $\partial \Omega$, and $\operatorname { deg } _ { B } [ f , \Omega , y ] = \operatorname { deg } _ { B } [ f , \Omega , z ]$ when $y$ and $z$ belong to the same component $C_i$ of $\mathbf{R} ^ { n } \backslash f ( \partial \Omega )$ (with the common value written $\operatorname { deg } _ { B } [ f , \Omega , C _ { i } ]$).
The existence and homotopy properties have many important applications in studying the existence and bifurcation of solutions of various types of equations.
Product theorem.
In 1934, J. Leray [a6] proved a useful product theorem for the Brouwer degree: let $f : \overline { \Omega } \rightarrow \mathbf{R} ^ { n }$ and $g : \overline { \Delta } \rightarrow {\bf R} ^ { n }$, with $\Delta \supset f ( \overline { \Omega } )$, be continuous functions such that $y \notin g \circ f ( \partial \Omega )$. Denoting by $C_i$ the bounded components of $\Delta \backslash f ( \partial \Omega )$, one has 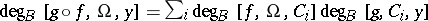 , where only finitely many terms are different from zero.
, where only finitely many terms are different from zero.
This result has deep applications in topology, for example the Jordan separation theorem: for homeomorphic compact subsets $K _ { 1 }$ and $K _ { 2 }$ of ${\bf R} ^ { n }$, the sets $\mathbf{R} ^ { n } \backslash K _ { 1 }$ and ${\bf R} ^ { n } \backslash K _ { 2 }$ have the same number of connected components.
Fixed-point theorems.
An easy consequence of the Brouwer degree is the following Knaster–Kuratowski–Mazurkiewicz fixed-point theorem, first stated and proved in 1929 [a4]: let $B [ R ] \subset \mathbf{R} ^ { n }$ be the closed ball of centre $0$ and radius $R$ and let $g : B [ R ] \rightarrow \mathbf{R} ^ { n }$ be a continuous function such that $g ( \partial B [ R ] ) \subset B[R]$. Then there is at least one $x \in B [ R ]$ such that $g ( x ) = x$.
The special case where $g : B [ R ] \rightarrow B [ R ]$ is the Brouwer fixed-point theorem [a2], which has many different and useful equivalent forms.
Degree of symmetric mappings.
Useful computational results hold under symmetry assumptions. The oldest one, which corresponds to $\mathbf{Z}_{2}$-symmetry, was conjectured by S.M. Ulam and proved by K. Borsuk in 1933 [a1]: let $\Omega$ be a bounded open symmetric neighbourhood of the origin in ${\bf R} ^ { n }$ and let $f : \overline { \Omega } \rightarrow \mathbf{R} ^ { n }$ be a continuous odd function such that $0 \notin f ( \partial \Omega )$; then $\text{deg}_B[ f , \Omega , 0 ]$ is odd.
This result and its more recent $S ^ { 1 }$-version are basic in critical point theory [a7].
Other approaches and extensions.
The Brouwer degree is a very versatile concept which can be defined through techniques of algebraic topology, differential topology or algebraic geometry. For example, if $f : S ^ { n } \rightarrow S ^ { n }$ is continuous and $f ^ { * } : H ^ { * } ( S ^ { n } ) \rightarrow H ^ { * } ( S ^ { n } )$ is the induced homomorphism on the homology groups of $S ^ { n }$ over $\mathbf{Z}$ (cf. also Homology group), then $H _ { n } ( S ^ { n } )$ is isomorphic to $\mathbf{Z}$ and hence $f _ { n } ^ { * }$ becomes multiplication by an integer, which is $d [ f , S ^ { n } , S ^ { n } ]$. If $\widetilde { f }$ is any continuous extension of $f$ to the closed unit ball $B ( 1 )$, then $d [ f , S ^ { n } , S ^ { n } ] = \operatorname { deg } _ { B } [ \tilde { f } , B ( 1 ) , 0 ]$.
In 1995, H. Brézis and L. Nirenberg [a10], [a11] defined a Brouwer degree for certain not necessarily continuous mappings $f$ belonging to a Sobolev or other function space.
Extensions of the Brouwer degree to various classes of mappings between infinite-dimensional spaces are also known. The most fundamental one is the Leray–Schauder degree, defined in 1934 for compact perturbations of the identity defined on the closure of a bounded open subset of a normed vector space (cf. also Degree of a mapping).
References
| [a1] | K. Borsuk, "Drei Sätze über die $n$-dimensionale euklidische Sphäre" Fundam. Math. , 21 (1933) pp. 177–190 |
| [a2] | L.E.J. Brouwer, "Ueber Abbildungen von Mannigfaltigkeiten" Math. Ann. , 71 (1912) pp. 97–115 |
| [a3] | J. Hadamard, "Sur quelques applications de l'indice de Kronecker" J. Tannery (ed.) , Introduction à la théorie des fonctions d'une variable , 2 , Hermann (1910) pp. 875–915 |
| [a4] | B. Knaster, C. Kuratowski, S. Mazurkiewicz, "Ein Beweis des Fixpunktsatzes für $n$-dimensionale Simplexe" Fundam. Math. , 14 (1929) pp. 132–137 |
| [a5] | L. Kronecker, "Ueber Systeme von Funktionen mehrerer Variabeln" Monatsber. Berlin Akad. (1869) pp. 159–193; 688–698 Zbl 02.0203.02 |
| [a6] | J. Leray, "Topologie des espaces abstraits de M. Banach" C.R. Acad. Sci. Paris , 200 (1935) pp. 1082–1084 Zbl 0011.16402 Zbl 61.0613.03 |
| [a7] | J. Mawhin, M. Willem, "Critical point theory and Hamiltonian systems" , Springer (1989) MR0982267 Zbl 0676.58017 |
| [a8] | M. Nagumo, "A theory of degree of mapping based on infinitesimal analysis" Amer. J. Math. , 73 (1951) pp. 485–496 MR0042696 Zbl 0043.17802 |
| [a9] | E. Zeidler, "Nonlinear functional analysis and its applications" , I , Springer (1986) MR0816732 Zbl 0583.47050 |
| [a10] | H. Brézis, L. Nirenberg, "Degree theory and BMO" Selecta Math. , 1 (1995) pp. 197–263 MR1354598 Zbl 0868.58017 |
| [a11] | H. Brézis, L. Nirenberg, "Degree theory and BMO" Selecta Math. , 2 (1996) pp. 1–60 MR1422201 Zbl 0868.58017 |
Brouwer degree. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brouwer_degree&oldid=49935