Difference between revisions of "Darbo fixed-point theorem"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 26 formulas out of 27 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | Another measure of non-compactness is the ball measure | + | Out of 27 formulas, 26 were replaced by TEX code.--> |
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
| + | The notion of "measure of non-compactness" was first introduced by C. Kuratowski [[#References|[a1]]]. For any bounded set $B$ in a [[Metric space|metric space]] its measure of non-compactness, denoted by $\alpha ( B )$, is defined to be the infimum of the positive numbers $d$ such that $B$ can be covered by a finite number of sets of diameter less than or equal to $d$. | ||
| + | |||
| + | Another measure of non-compactness is the ball measure $\mu ( B )$, or Hausdorff measure, which is defined as the infimum of the positive numbers $r$ such that $B$ can be covered by a finite number of balls of radii smaller than $r$. See also [[Hausdorff measure|Hausdorff measure]]. | ||
Roughly speaking, a measure of non-compactness is some function defined on the family of all non-empty bounded subsets of a given metric space such that it is equal to zero on the whole family of relatively compact sets. | Roughly speaking, a measure of non-compactness is some function defined on the family of all non-empty bounded subsets of a given metric space such that it is equal to zero on the whole family of relatively compact sets. | ||
| − | G. Darbo used a measure of non-compactness to investigate operators whose properties can be characterized as being intermediate between those of contraction and compact mappings (cf. also [[Compact mapping|Compact mapping]]; [[Compact operator|Compact operator]]; [[Contraction(2)|Contraction]]). He was the first to use the index | + | G. Darbo used a measure of non-compactness to investigate operators whose properties can be characterized as being intermediate between those of contraction and compact mappings (cf. also [[Compact mapping|Compact mapping]]; [[Compact operator|Compact operator]]; [[Contraction(2)|Contraction]]). He was the first to use the index $\alpha$ in the theory of fixed points [[#References|[a2]]]. Darbo's fixed-point theorem is a generalization of the well-known Schauder fixed-point theorem (cf. also [[Schauder theorem|Schauder theorem]]). It states that if $S$ is a non-empty bounded closed convex subset of a [[Banach space|Banach space]] $X$ and $T : S \rightarrow S$ is a [[Continuous mapping|continuous mapping]] such that for any set $E \subset S$, |
| − | + | \begin{equation} \tag{a1} \alpha ( T E ) \leq k \alpha ( E ), \end{equation} | |
| − | where | + | where $k$ is a constant, $0 \leq k < 1$, then $T$ has a [[Fixed point|fixed point]]. This theorem is true for the measure $\mu$ also. |
| − | Note that every completely-continuous mapping (or [[Compact mapping|compact mapping]]; cf. also [[Completely-continuous operator|Completely-continuous operator]]) satisfies (a1) with | + | Note that every completely-continuous mapping (or [[Compact mapping|compact mapping]]; cf. also [[Completely-continuous operator|Completely-continuous operator]]) satisfies (a1) with $k = 0$, while all Lipschitz mappings with constant $k$ (cf. [[Lipschitz condition|Lipschitz condition]]) also satisfy (a1). Further, mappings that are not completely continuous but satisfy the condition (a1) are of the form $T = T _ { 1 } + T _ { 2 }$, where $T _ { 1 }$ is completely continuous and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130020/d13002024.png"/> satisfies the Lipschitz condition with constant $k$. The significance of this type of mapping is due to the fact that compactness of either the domain or the range is not required. |
| − | Methods for determining the value of | + | Methods for determining the value of $\mu ( B )$ for a given set $B$ in a Banach space are given in [[#References|[a3]]]. |
Darbo's fixed-point theorem is useful in establishing the existence of solutions of various classes of differential equations, especially for implicit differential equations, integral equations and integro-differential equations, see [[#References|[a3]]]. It is also used to study the controllability problem for dynamical systems represented by implicit differential equations [[#References|[a4]]]. | Darbo's fixed-point theorem is useful in establishing the existence of solutions of various classes of differential equations, especially for implicit differential equations, integral equations and integro-differential equations, see [[#References|[a3]]]. It is also used to study the controllability problem for dynamical systems represented by implicit differential equations [[#References|[a4]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> C. Kuratowski, "Sur les espaces complets" ''Fundam. Math.'' , '''15''' (1930) pp. 301–309</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> G. Darbo, "Punti uniti in transformazioni a condominio non compacto" ''Rend. Sem. Mat. Univ. Padova'' , '''24''' (1955) pp. 84–92</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J. Banas, K. Goebel, "Measure of noncompactness in Banach spaces" , M. Dekker (1980)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> K. Balachandran, J.P. Dauer, "Controllability of nonlinear systems via fixed point theorems" ''J. Optim. Th. Appl.'' , '''53''' (1987) pp. 345–352</td></tr></table> |
Revision as of 15:30, 1 July 2020
The notion of "measure of non-compactness" was first introduced by C. Kuratowski [a1]. For any bounded set $B$ in a metric space its measure of non-compactness, denoted by $\alpha ( B )$, is defined to be the infimum of the positive numbers $d$ such that $B$ can be covered by a finite number of sets of diameter less than or equal to $d$.
Another measure of non-compactness is the ball measure $\mu ( B )$, or Hausdorff measure, which is defined as the infimum of the positive numbers $r$ such that $B$ can be covered by a finite number of balls of radii smaller than $r$. See also Hausdorff measure.
Roughly speaking, a measure of non-compactness is some function defined on the family of all non-empty bounded subsets of a given metric space such that it is equal to zero on the whole family of relatively compact sets.
G. Darbo used a measure of non-compactness to investigate operators whose properties can be characterized as being intermediate between those of contraction and compact mappings (cf. also Compact mapping; Compact operator; Contraction). He was the first to use the index $\alpha$ in the theory of fixed points [a2]. Darbo's fixed-point theorem is a generalization of the well-known Schauder fixed-point theorem (cf. also Schauder theorem). It states that if $S$ is a non-empty bounded closed convex subset of a Banach space $X$ and $T : S \rightarrow S$ is a continuous mapping such that for any set $E \subset S$,
\begin{equation} \tag{a1} \alpha ( T E ) \leq k \alpha ( E ), \end{equation}
where $k$ is a constant, $0 \leq k < 1$, then $T$ has a fixed point. This theorem is true for the measure $\mu$ also.
Note that every completely-continuous mapping (or compact mapping; cf. also Completely-continuous operator) satisfies (a1) with $k = 0$, while all Lipschitz mappings with constant $k$ (cf. Lipschitz condition) also satisfy (a1). Further, mappings that are not completely continuous but satisfy the condition (a1) are of the form $T = T _ { 1 } + T _ { 2 }$, where $T _ { 1 }$ is completely continuous and 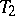 satisfies the Lipschitz condition with constant $k$. The significance of this type of mapping is due to the fact that compactness of either the domain or the range is not required.
satisfies the Lipschitz condition with constant $k$. The significance of this type of mapping is due to the fact that compactness of either the domain or the range is not required.
Methods for determining the value of $\mu ( B )$ for a given set $B$ in a Banach space are given in [a3].
Darbo's fixed-point theorem is useful in establishing the existence of solutions of various classes of differential equations, especially for implicit differential equations, integral equations and integro-differential equations, see [a3]. It is also used to study the controllability problem for dynamical systems represented by implicit differential equations [a4].
References
| [a1] | C. Kuratowski, "Sur les espaces complets" Fundam. Math. , 15 (1930) pp. 301–309 |
| [a2] | G. Darbo, "Punti uniti in transformazioni a condominio non compacto" Rend. Sem. Mat. Univ. Padova , 24 (1955) pp. 84–92 |
| [a3] | J. Banas, K. Goebel, "Measure of noncompactness in Banach spaces" , M. Dekker (1980) |
| [a4] | K. Balachandran, J.P. Dauer, "Controllability of nonlinear systems via fixed point theorems" J. Optim. Th. Appl. , 53 (1987) pp. 345–352 |
Darbo fixed-point theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darbo_fixed-point_theorem&oldid=49884