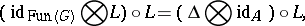|
|
| Line 1: |
Line 1: |
| − | A [[unital algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200301.png" /> that is a [[co-module]] for a quantum group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200302.png" /> (cf. [[Quantum groups|Quantum groups]]) and for which the structure mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200303.png" /> is an algebra homomorphism, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200304.png" /> is a co-module algebra [[#References|[a1]]]. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200305.png" /> is a deformation of the [[Poisson algebra|Poisson algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200306.png" />, of a Poisson–Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200307.png" />, endowed with the structure of a Hopf algebra with a co-multiplication <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200308.png" /> and a co-unit <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200309.png" />. Often, both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003011.png" /> can also be equipped with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003013.png" />-involution. The left co-action <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003014.png" /> satisfies
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003015.png" /></td> </tr></table>
| + | Out of 64 formulas, 61 were replaced by TEX code.--> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003016.png" /></td> </tr></table>
| + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | A [[unital algebra]] $A$ that is a [[co-module]] for a quantum group $\operatorname{Fun}_{q} ( G )$ (cf. [[Quantum groups|Quantum groups]]) and for which the structure mapping $L : A \rightarrow \operatorname { Fun } _ { q } ( G ) \otimes A$ is an algebra homomorphism, i.e., $A$ is a co-module algebra [[#References|[a1]]]. Here, $\operatorname{Fun}_{q} ( G )$ is a deformation of the [[Poisson algebra|Poisson algebra]] $\operatorname{Fun}( G )$, of a Poisson–Lie group $G$, endowed with the structure of a Hopf algebra with a co-multiplication $\Delta$ and a co-unit <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q1200309.png"/>. Often, both $A$ and $\operatorname{Fun}_{q} ( G )$ can also be equipped with a $*$-involution. The left co-action $L$ satisfies |
| | | | |
| − | These relations should be modified correspondingly for a right co-action. In the dual picture, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003017.png" /> is the deformed universal enveloping algebra of the Lie algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003019.png" /> is a non-degenerate dual pairing between the Hopf algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003021.png" />, then the prescription <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003022.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003024.png" />, defines a right action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003025.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003026.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003027.png" />) and one has
| + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003015.png"/></td> </tr></table> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003028.png" /></td> </tr></table>
| + | \begin{equation*} ( \epsilon \bigotimes \operatorname{id} _ { A } ) \circ L = \operatorname{id} _ { A }. \end{equation*} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003029.png" /> is the multiplication in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003031.png" /> is the co-multiplication in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003032.png" />. Typically, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003033.png" /> is a deformation of the Poisson algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003034.png" /> (frequently called the quantization of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003035.png" />), where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003036.png" /> is a Poisson manifold and, at the same time, a left homogeneous space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003037.png" /> with the left action <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003038.png" /> a Poisson mapping.
| + | These relations should be modified correspondingly for a right co-action. In the dual picture, if ${\cal U} _ { q } ( \mathfrak { g } )$ is the deformed universal enveloping algebra of the Lie algebra $\frak g$ and $\langle \, .\, ,\, . \, \rangle$ is a non-degenerate dual pairing between the Hopf algebras ${\cal U} _ { q } ( \mathfrak { g } )$ and $\operatorname{Fun}_{q} ( G )$, then the prescription $X\cdot f = ( \langle X , \cdot \rangle \otimes \operatorname {id} _ { A } ) L ( f )$, with $X \in \mathcal U _ { q } ( \mathfrak { g } )$ and $f \in A$, defines a right action of ${\cal U} _ { q } ( \mathfrak { g } )$ on $A$ ($X.( Y . f ) = ( Y X ) . f$) and one has |
| | | | |
| − | It is not quite clear how to translate into purely algebraic terms the property that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003039.png" /> is a homogeneous space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003040.png" />. One possibility is to require that only multiples of the unit <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003041.png" /> satisfy <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003042.png" />. A stronger condition requires the existence of a linear functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003043.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003044.png" /> while the linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003045.png" /> be injective. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003046.png" /> can be considered as a base point.
| + | \begin{equation*} X. ( f g ) = \mu ( \Delta X . ( f \bigotimes g ) ), \end{equation*} |
| | | | |
| − | The still stronger requirement that, in addition, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003047.png" /> be a homomorphism (a so-called classical point) holds when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003048.png" /> is a quantization of a Poisson homogeneous space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003049.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003050.png" /> a Poisson–Lie subgroup. The quantum homogeneous space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003051.png" /> is defined as the subalgebra in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003052.png" /> formed by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003053.png" />-invariant elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003054.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003055.png" /> where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003056.png" /> is a Hopf-algebra homomorphism.
| + | where $\mu : A \otimes A \rightarrow A$ is the multiplication in $A$ and $\Delta$ is the co-multiplication in $\mathcal{U} ( \mathfrak { g } )$. Typically, $A$ is a deformation of the Poisson algebra $\operatorname { Fun } ( M )$ (frequently called the quantization of $M$), where $M$ is a Poisson manifold and, at the same time, a left homogeneous space of $G$ with the left action $G \times M \rightarrow M$ a Poisson mapping. |
| | | | |
| − | A richer class of examples is provided by quantization of orbits of the dressing transformation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003057.png" />, acting on its dual Poisson–Lie group (also called the generalized Pontryagin dual) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003058.png" />. The best studied cases concern the compact and solvable factors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003060.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003061.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003062.png" /> are mutually dual) in the Iwasawa decomposition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003063.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q120/q120030/q12003064.png" /> is a simple complex [[Lie group|Lie group]]. One obtains this way, among others, the [[Quantum sphere|quantum sphere]] and, more generally, [[Quantum Grassmannian|quantum Grassmannian]] and quantum flag manifolds. | + | It is not quite clear how to translate into purely algebraic terms the property that $M$ is a homogeneous space of $G$. One possibility is to require that only multiples of the unit $1 \in A$ satisfy $L ( f ) = 1 \otimes f$. A stronger condition requires the existence of a linear functional $\varphi \in A ^ { * }$ such that $\varphi ( 1 ) = 1$ while the linear mapping $\psi = ( \text { id } \otimes \varphi ) \circ L : A \rightarrow \operatorname { Fun } _ { q } ( G )$ be injective. Then $\varphi$ can be considered as a base point. |
| | + | |
| | + | The still stronger requirement that, in addition, $\varphi$ be a homomorphism (a so-called classical point) holds when $A$ is a quantization of a Poisson homogeneous space $M = G / H$ with $H \subset G$ a Poisson–Lie subgroup. The quantum homogeneous space $\operatorname { Fun } _ { q } ( G / H )$ is defined as the subalgebra in $\operatorname{Fun}_{q} ( G )$ formed by $H$-invariant elements $f$, $( \text { id } \otimes \pi ) \Delta f = f \otimes 1$ where $\pi : \operatorname { Fun } _ { q } ( G ) \rightarrow \operatorname { Fun } _ { q } ( H )$ is a Hopf-algebra homomorphism. |
| | + | |
| | + | A richer class of examples is provided by quantization of orbits of the dressing transformation of $G$, acting on its dual Poisson–Lie group (also called the generalized Pontryagin dual) $G ^ { * }$. The best studied cases concern the compact and solvable factors $K$ and $AN$ ($K$ and $AN$ are mutually dual) in the Iwasawa decomposition $\mathfrak { G } = K.AN$, where $\mathfrak{G}$ is a simple complex [[Lie group|Lie group]]. One obtains this way, among others, the [[Quantum sphere|quantum sphere]] and, more generally, [[Quantum Grassmannian|quantum Grassmannian]] and quantum flag manifolds. |
| | | | |
| | There is a vast amount of literature on this subject. The survey book [[#References|[a2]]] contains a rich list of references. | | There is a vast amount of literature on this subject. The survey book [[#References|[a2]]] contains a rich list of references. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Abe, "Hopf algebras" , Cambridge Univ. Press (1977)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V. Chari, A. Pressley, "A guide to quantum groups" , Cambridge Univ. Press (1994)</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> E. Abe, "Hopf algebras" , Cambridge Univ. Press (1977)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> V. Chari, A. Pressley, "A guide to quantum groups" , Cambridge Univ. Press (1994)</td></tr></table> |
A unital algebra $A$ that is a co-module for a quantum group $\operatorname{Fun}_{q} ( G )$ (cf. Quantum groups) and for which the structure mapping $L : A \rightarrow \operatorname { Fun } _ { q } ( G ) \otimes A$ is an algebra homomorphism, i.e., $A$ is a co-module algebra [a1]. Here, $\operatorname{Fun}_{q} ( G )$ is a deformation of the Poisson algebra $\operatorname{Fun}( G )$, of a Poisson–Lie group $G$, endowed with the structure of a Hopf algebra with a co-multiplication $\Delta$ and a co-unit  . Often, both $A$ and $\operatorname{Fun}_{q} ( G )$ can also be equipped with a $*$-involution. The left co-action $L$ satisfies
. Often, both $A$ and $\operatorname{Fun}_{q} ( G )$ can also be equipped with a $*$-involution. The left co-action $L$ satisfies
\begin{equation*} ( \epsilon \bigotimes \operatorname{id} _ { A } ) \circ L = \operatorname{id} _ { A }. \end{equation*}
These relations should be modified correspondingly for a right co-action. In the dual picture, if ${\cal U} _ { q } ( \mathfrak { g } )$ is the deformed universal enveloping algebra of the Lie algebra $\frak g$ and $\langle \, .\, ,\, . \, \rangle$ is a non-degenerate dual pairing between the Hopf algebras ${\cal U} _ { q } ( \mathfrak { g } )$ and $\operatorname{Fun}_{q} ( G )$, then the prescription $X\cdot f = ( \langle X , \cdot \rangle \otimes \operatorname {id} _ { A } ) L ( f )$, with $X \in \mathcal U _ { q } ( \mathfrak { g } )$ and $f \in A$, defines a right action of ${\cal U} _ { q } ( \mathfrak { g } )$ on $A$ ($X.( Y . f ) = ( Y X ) . f$) and one has
\begin{equation*} X. ( f g ) = \mu ( \Delta X . ( f \bigotimes g ) ), \end{equation*}
where $\mu : A \otimes A \rightarrow A$ is the multiplication in $A$ and $\Delta$ is the co-multiplication in $\mathcal{U} ( \mathfrak { g } )$. Typically, $A$ is a deformation of the Poisson algebra $\operatorname { Fun } ( M )$ (frequently called the quantization of $M$), where $M$ is a Poisson manifold and, at the same time, a left homogeneous space of $G$ with the left action $G \times M \rightarrow M$ a Poisson mapping.
It is not quite clear how to translate into purely algebraic terms the property that $M$ is a homogeneous space of $G$. One possibility is to require that only multiples of the unit $1 \in A$ satisfy $L ( f ) = 1 \otimes f$. A stronger condition requires the existence of a linear functional $\varphi \in A ^ { * }$ such that $\varphi ( 1 ) = 1$ while the linear mapping $\psi = ( \text { id } \otimes \varphi ) \circ L : A \rightarrow \operatorname { Fun } _ { q } ( G )$ be injective. Then $\varphi$ can be considered as a base point.
The still stronger requirement that, in addition, $\varphi$ be a homomorphism (a so-called classical point) holds when $A$ is a quantization of a Poisson homogeneous space $M = G / H$ with $H \subset G$ a Poisson–Lie subgroup. The quantum homogeneous space $\operatorname { Fun } _ { q } ( G / H )$ is defined as the subalgebra in $\operatorname{Fun}_{q} ( G )$ formed by $H$-invariant elements $f$, $( \text { id } \otimes \pi ) \Delta f = f \otimes 1$ where $\pi : \operatorname { Fun } _ { q } ( G ) \rightarrow \operatorname { Fun } _ { q } ( H )$ is a Hopf-algebra homomorphism.
A richer class of examples is provided by quantization of orbits of the dressing transformation of $G$, acting on its dual Poisson–Lie group (also called the generalized Pontryagin dual) $G ^ { * }$. The best studied cases concern the compact and solvable factors $K$ and $AN$ ($K$ and $AN$ are mutually dual) in the Iwasawa decomposition $\mathfrak { G } = K.AN$, where $\mathfrak{G}$ is a simple complex Lie group. One obtains this way, among others, the quantum sphere and, more generally, quantum Grassmannian and quantum flag manifolds.
There is a vast amount of literature on this subject. The survey book [a2] contains a rich list of references.
References
| [a1] | E. Abe, "Hopf algebras" , Cambridge Univ. Press (1977) |
| [a2] | V. Chari, A. Pressley, "A guide to quantum groups" , Cambridge Univ. Press (1994) |
 . Often, both $A$ and $\operatorname{Fun}_{q} ( G )$ can also be equipped with a $*$-involution. The left co-action $L$ satisfies
. Often, both $A$ and $\operatorname{Fun}_{q} ( G )$ can also be equipped with a $*$-involution. The left co-action $L$ satisfies