Difference between revisions of "Weyl-Otsuki space"
Ulf Rehmann (talk | contribs) m (moved Weyl–Otsuki space to Weyl-Otsuki space: ascii title) |
m (AUTOMATIC EDIT (latexlist): Replaced 43 formulas out of 49 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 49 formulas, 43 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''Otsuki–Weyl space'' | ''Otsuki–Weyl space'' | ||
| − | An Otsuki space [[#References|[a6]]], [[#References|[a7]]] is a [[Manifold|manifold]] | + | An Otsuki space [[#References|[a6]]], [[#References|[a7]]] is a [[Manifold|manifold]] $M$ endowed with two different linear connections $\square ^ { '' } \Gamma$ and $\square ^ { \prime } \Gamma$ (cf. also [[Connections on a manifold|Connections on a manifold]]) and a non-degenerate $( 1,1 )$ tensor field $P$ of constant rank (cf. also [[Tensor analysis|tensor analysis]]), where the connection coefficients $\square ^ { \prime \prime } \Gamma _ { j k } ^ { i } ( x )$, $x \in M$, are used in the computation of the contravariant, and the $\square ^ { \prime } \Gamma _ { j k } ^ { i } ( x )$ in the computation of the covariant, components of the invariant (covariant) differential of a tensor (vector). For a tensor field $T$ of type $( 1,1 )$, the invariant differential $DT$ and the covariant differential $\nabla T$ have the following forms |
| − | + | \begin{equation*} D T _ { j } ^ { i } = \nabla _ { k } T _ { j } ^ { i } d x ^ { k } = \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120100/w12010014.png"/></td> </tr></table> |
| − | + | $\square ^ { \prime } \Gamma$ and $\square ^ { '' } \Gamma$ are connected by the relation | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120100/w12010017.png"/></td> </tr></table> |
| − | Thus, | + | Thus, $\square ^ { '' } \Gamma$ and $P$ determine $\square ^ { \prime } \Gamma$. T. Otsuki calls these a general connection. For $P ^ { i } _ { r } = \delta ^ { i }_r$ one obtains $\square ^ { \prime } \Gamma = \square ^ { \prime \prime } \Gamma$ and the usual invariant differential. |
| − | If | + | If $M$ is endowed also with a [[Riemannian metric|Riemannian metric]] $g$, then $\square ^ { \prime \prime } \Gamma _ { j k } ^ { i } ( x )$ may be the [[Christoffel symbol|Christoffel symbol]] $\{ \square _ { j k } ^ { i } \}$. |
| − | In a Weyl space | + | In a Weyl space $W ^ { n } = ( M , g , \gamma )$ one has $\nabla _ { i g j k } = \gamma _ { i g j k }$. A Weyl–Otsuki space $W - O _ { n }$ [[#References|[a1]]] is a $W ^ { m }$ endowed with an Otsuki connection. The $\square ^ { \prime \prime } \Gamma _ { r k } ^ { t }$ are defined here as |
| − | + | \begin{equation*} \square ^ { \prime \prime } \Gamma _ { r k } ^ { t } = \{ \square _ { r k } ^ { t } \} - \frac { 1 } { 2 } g ^ { t s } ( \gamma _ { k } m _ { r s } + \gamma _ { r } m _ { s k } - \gamma _ { s } m _ { r k } ), \end{equation*} | |
| − | + | \begin{equation*} m _ { r s } = g _ { ij} Q _ { r } ^ { i } Q _ { s } ^ { j }, \end{equation*} | |
| − | where | + | where $Q$ is the inverse of $P$. $W - O _ { n }$ spaces were studied mainly by A. Moór [[#References|[a2]]], [[#References|[a3]]]. |
| − | He extended the Otsuki connection also to affine and metrical line-element spaces, obtaining Finsler–Otsuki spaces | + | He extended the Otsuki connection also to affine and metrical line-element spaces, obtaining Finsler–Otsuki spaces $F - O _ { n }$ [[#References|[a4]]], [[#References|[a5]]] with invariant differential |
| − | + | \begin{equation*} D T_j^i = \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120100/w12010039.png"/></td> </tr></table> |
| − | Here, all objects depend on the line-element | + | Here, all objects depend on the line-element $( x , \dot { x } )$, the $T$, $P$, $\square ^ { \prime } \Gamma$, $\square ^ { '' } \Gamma$ are homogeneous of order $O$, and $C$ is a tensor. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> A. Moór, "Otsukische Übertragung mit rekurrenter Maß tensor" ''Acta Sci. Math.'' , '''40''' (1978) pp. 129–142</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. Moór, "Über verschiedene geodätische Abweichungen in Weyl–Otsukischen Räumen" ''Publ. Math. Debrecen'' , '''28''' (1981) pp. 247–258</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> A. Moór, "Über Transformationsgruppen in Weyl–Otsukischen Räumen" ''Publ. Math. Debrecen'' , '''29''' (1982) pp. 241–250</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> A. Moór, "Über die Begründung von Finsler–Otschukischen Räumen und ihre Dualität" ''Tensor N.S.'' , '''37''' (1982) pp. 121–129</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> A. Moór, "Über spezielle Finsler–Otsukische Räume" ''Publ. Math. Debrecen'' , '''31''' (1984) pp. 185–196</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> T. Otsuki, "On general connections. I" ''Math. J. Okayama Univ.'' , '''9''' (1959-60) pp. 99–164</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> T. Otsuki, "On metric general connections" ''Proc. Japan Acad.'' , '''37''' (1961) pp. 183–188</td></tr></table> |
Revision as of 15:19, 1 July 2020
Otsuki–Weyl space
An Otsuki space [a6], [a7] is a manifold $M$ endowed with two different linear connections $\square ^ { '' } \Gamma$ and $\square ^ { \prime } \Gamma$ (cf. also Connections on a manifold) and a non-degenerate $( 1,1 )$ tensor field $P$ of constant rank (cf. also tensor analysis), where the connection coefficients $\square ^ { \prime \prime } \Gamma _ { j k } ^ { i } ( x )$, $x \in M$, are used in the computation of the contravariant, and the $\square ^ { \prime } \Gamma _ { j k } ^ { i } ( x )$ in the computation of the covariant, components of the invariant (covariant) differential of a tensor (vector). For a tensor field $T$ of type $( 1,1 )$, the invariant differential $DT$ and the covariant differential $\nabla T$ have the following forms
\begin{equation*} D T _ { j } ^ { i } = \nabla _ { k } T _ { j } ^ { i } d x ^ { k } = \end{equation*}
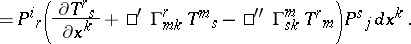 |
$\square ^ { \prime } \Gamma$ and $\square ^ { '' } \Gamma$ are connected by the relation
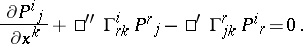 |
Thus, $\square ^ { '' } \Gamma$ and $P$ determine $\square ^ { \prime } \Gamma$. T. Otsuki calls these a general connection. For $P ^ { i } _ { r } = \delta ^ { i }_r$ one obtains $\square ^ { \prime } \Gamma = \square ^ { \prime \prime } \Gamma$ and the usual invariant differential.
If $M$ is endowed also with a Riemannian metric $g$, then $\square ^ { \prime \prime } \Gamma _ { j k } ^ { i } ( x )$ may be the Christoffel symbol $\{ \square _ { j k } ^ { i } \}$.
In a Weyl space $W ^ { n } = ( M , g , \gamma )$ one has $\nabla _ { i g j k } = \gamma _ { i g j k }$. A Weyl–Otsuki space $W - O _ { n }$ [a1] is a $W ^ { m }$ endowed with an Otsuki connection. The $\square ^ { \prime \prime } \Gamma _ { r k } ^ { t }$ are defined here as
\begin{equation*} \square ^ { \prime \prime } \Gamma _ { r k } ^ { t } = \{ \square _ { r k } ^ { t } \} - \frac { 1 } { 2 } g ^ { t s } ( \gamma _ { k } m _ { r s } + \gamma _ { r } m _ { s k } - \gamma _ { s } m _ { r k } ), \end{equation*}
\begin{equation*} m _ { r s } = g _ { ij} Q _ { r } ^ { i } Q _ { s } ^ { j }, \end{equation*}
where $Q$ is the inverse of $P$. $W - O _ { n }$ spaces were studied mainly by A. Moór [a2], [a3].
He extended the Otsuki connection also to affine and metrical line-element spaces, obtaining Finsler–Otsuki spaces $F - O _ { n }$ [a4], [a5] with invariant differential
\begin{equation*} D T_j^i = \end{equation*}
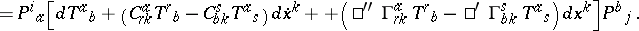 |
Here, all objects depend on the line-element $( x , \dot { x } )$, the $T$, $P$, $\square ^ { \prime } \Gamma$, $\square ^ { '' } \Gamma$ are homogeneous of order $O$, and $C$ is a tensor.
References
| [a1] | A. Moór, "Otsukische Übertragung mit rekurrenter Maß tensor" Acta Sci. Math. , 40 (1978) pp. 129–142 |
| [a2] | A. Moór, "Über verschiedene geodätische Abweichungen in Weyl–Otsukischen Räumen" Publ. Math. Debrecen , 28 (1981) pp. 247–258 |
| [a3] | A. Moór, "Über Transformationsgruppen in Weyl–Otsukischen Räumen" Publ. Math. Debrecen , 29 (1982) pp. 241–250 |
| [a4] | A. Moór, "Über die Begründung von Finsler–Otschukischen Räumen und ihre Dualität" Tensor N.S. , 37 (1982) pp. 121–129 |
| [a5] | A. Moór, "Über spezielle Finsler–Otsukische Räume" Publ. Math. Debrecen , 31 (1984) pp. 185–196 |
| [a6] | T. Otsuki, "On general connections. I" Math. J. Okayama Univ. , 9 (1959-60) pp. 99–164 |
| [a7] | T. Otsuki, "On metric general connections" Proc. Japan Acad. , 37 (1961) pp. 183–188 |
Weyl-Otsuki space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl-Otsuki_space&oldid=49873