Difference between revisions of "Sequential analysis"
Ulf Rehmann (talk | contribs) m (Undo revision 48674 by Ulf Rehmann (talk)) Tag: Undo |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | s0846001.png | ||
| + | $#A+1 = 209 n = 0 | ||
| + | $#C+1 = 209 : ~/encyclopedia/old_files/data/S084/S.0804600 Sequential analysis | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
{{MSC|62L10}} | {{MSC|62L10}} | ||
| Line 5: | Line 17: | ||
A branch of mathematical statistics. Its characteristic feature is that the number of observations to be performed (the moment of termination of the observations) is not fixed in advance but is chosen in the course of the experiment depending upon the results that are obtained. The intensive development and application of sequential methods in statistics was due to the work of A. Wald. He established that in the problem of decision (based on the results of independent observations) between two simple hypotheses the so-called sequential probability ratio test gives a considerable improvement in terms of the average number of observations required in comparison with the most-powerful test for deciding between two hypotheses (determined by the Neyman–Pearson lemma) for a fixed sample size and the same error probabilities. | A branch of mathematical statistics. Its characteristic feature is that the number of observations to be performed (the moment of termination of the observations) is not fixed in advance but is chosen in the course of the experiment depending upon the results that are obtained. The intensive development and application of sequential methods in statistics was due to the work of A. Wald. He established that in the problem of decision (based on the results of independent observations) between two simple hypotheses the so-called sequential probability ratio test gives a considerable improvement in terms of the average number of observations required in comparison with the most-powerful test for deciding between two hypotheses (determined by the Neyman–Pearson lemma) for a fixed sample size and the same error probabilities. | ||
| − | The basic principles of sequential analysis consist of the following. Let | + | The basic principles of sequential analysis consist of the following. Let $ \xi _ {1} , \xi _ {2} \dots $ |
| + | be a sequence of independent identically-distributed random variables with distribution function $ F _ \theta ( x) = {\mathsf P} _ \theta \{ \xi _ {1} \leq x \} $ | ||
| + | which depends on an unknown parameter $ \theta $ | ||
| + | belonging to some parameter set $ \Theta $. | ||
| + | The problem consists of making a certain decision as to the true value of the unknown parameter $ \theta $, | ||
| + | based on the results of observations. | ||
| − | A space | + | A space $ D $ |
| + | of terminal final decisions $ d $( | ||
| + | for the values of the parameter $ \theta $) | ||
| + | and a termination rule $ \tau $ | ||
| + | which determines the time when the observations are stopped and the terminal decision is taken, lie at the basis of any statistical decision problem. In classical methods the time $ \tau $ | ||
| + | is non-random and is fixed in advance; in sequential methods $ \tau $ | ||
| + | is a random variable independent of the "future" (a Markovian time, a stopping time). Formally, let $ {\mathcal F} _ {n} = \sigma \{ \omega : {\xi _ {1} \dots \xi _ {n} } \} $ | ||
| + | be the $ \sigma $- | ||
| + | algebra generated by the random variables $ \xi _ {1} \dots \xi _ {n} $. | ||
| + | A random variable $ \tau = \tau ( \omega ) $ | ||
| + | assuming the values $ 0 \dots + \infty $ | ||
| + | is called a Markovian time if the event $ \{ \tau \leq n \} \in {\mathcal F} _ {n} $ | ||
| + | for any $ n \geq 0 $( | ||
| + | $ {\mathcal F} _ {0} = \{ \emptyset , \Omega \} $). | ||
| + | Let $ {\mathcal F} _ \tau $ | ||
| + | be the family of all measurable sets $ A $ | ||
| + | such that $ A \cap \{ \tau \leq n \} \in {\mathcal F} _ {n} $ | ||
| + | for any $ n \geq 0 $( | ||
| + | cf. also [[Markov moment|Markov moment]]). If $ {\mathcal F} _ {n} $ | ||
| + | is interpreted as the set of events observed up to some random time $ n $( | ||
| + | inclusive), then $ {\mathcal F} _ \tau $ | ||
| + | can be interpreted as the set of events observed up to the time $ \tau $( | ||
| + | inclusive). A terminal decision $ d = d ( \omega ) $ | ||
| + | is an $ {\mathcal F} _ \tau $- | ||
| + | measurable function with values in $ D $. | ||
| + | A pair $ \delta = ( \tau , d ) $ | ||
| + | of such functions is called a (sequential) decision rule. | ||
| − | In order to choose the "optimal" decision rule among all decision rules one usually defines a risk function | + | In order to choose the "optimal" decision rule among all decision rules one usually defines a risk function $ W ( \tau , \theta , d ) $ |
| + | and considers the mathematical expectation $ {\mathsf E} _ \theta W ( \tau , \theta , d ) $. | ||
| + | There are different approaches to defining the optimal decision rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $. | ||
| + | One of them, the Bayesian approach, is based on the assumption that the parameter $ \theta $ | ||
| + | is a random variable with a priori distribution $ \pi = \pi ( d \theta ) $. | ||
| + | Then one can speak of the $ \pi $- | ||
| + | risk | ||
| − | + | $$ | |
| + | R ^ \delta ( \pi ) = \int\limits _ \Theta {\mathsf E} _ \theta W | ||
| + | ( \tau , \theta , d ) \pi ( d \theta ) | ||
| + | $$ | ||
| − | and one calls a rule | + | and one calls a rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $ |
| + | the optimal Bayesian (or $ \pi $- | ||
| + | optimal) solution if $ R ^ {\delta * } ( \pi ) \leq R ^ \delta ( \pi ) $ | ||
| + | for any other (admissible) rule. The most widely used form of the risk function $ W ( \tau , \theta , d ) $ | ||
| + | is $ c \tau + W _ {1} ( \theta , d ) $, | ||
| + | where the constant $ c \geq 0 $ | ||
| + | is interpreted as the cost of a unit observation and $ W _ {1} ( \theta , d ) $ | ||
| + | is a loss function resulting from the terminal decision. | ||
| − | In Bayesian problems it is usually not difficult to find the terminal solution | + | In Bayesian problems it is usually not difficult to find the terminal solution $ d ^ {*} $; |
| + | thus the main efforts are concentrated on finding the optimal termination time $ \tau ^ {*} $. | ||
| + | Moreover, the majority of problems of sequential analysis fall into the following pattern of "optimal termination rules" . | ||
| − | Let | + | Let $ X = ( x _ {n} , {\mathcal F} _ {n} , {\mathsf P} _ {x} ) $, |
| + | $ n \geq 0 $, | ||
| + | $ x \in E $, | ||
| + | be a Markov chain in the state space $ ( E , {\mathcal B} ) $, | ||
| + | where $ x _ {n} $ | ||
| + | is the state of the chain at the time $ n $, | ||
| + | the $ \sigma $- | ||
| + | algebra $ {\mathcal F} _ {n} $ | ||
| + | is interpreted as the set of events observed up to the time $ n $( | ||
| + | inclusive), and $ {\mathsf P} _ {x} $ | ||
| + | is a probability distribution corresponding to the initial state $ x \in E $. | ||
| + | It is assumed that by stopping the observation at the time $ n $ | ||
| + | one obtains the gain $ g ( x _ {n} ) $. | ||
| + | Then the average gain resulting from termination at time $ \tau $ | ||
| + | is $ {\mathsf E} _ {x} g ( x _ \tau ) $, | ||
| + | where $ x $ | ||
| + | is the initial state. The function $ s ( x) = \sup {\mathsf E} _ {x} g ( x _ \tau ) $, | ||
| + | where the supremum is taken over all (finite) termination times $ \tau $, | ||
| + | is called the cost, and the time $ \tau _ \epsilon $ | ||
| + | for which $ s ( x) \leq {\mathsf E} g ( x _ \tau ) + \epsilon $ | ||
| + | for all $ x \in E $ | ||
| + | is called the $ \epsilon $- | ||
| + | optimal stopping time. $ 0 $- | ||
| + | optimal times are called optimal. The main problems in the theory of "optimal stopping rules" are the following: What is the structure of the cost $ s ( x) $, | ||
| + | how to find it, when do $ \epsilon $- | ||
| + | optimal and optimal times exist, and what is their structure? One of the typical results concerning these questions is discussed below. | ||
| − | Let the function | + | Let the function $ g ( x) $ |
| + | be bounded: $ | g ( x) | \leq c < \infty $. | ||
| + | Then the cost $ s ( x) $ | ||
| + | is the least excessive majorant of $ g ( x) $, | ||
| + | i.e. the smallest of the functions $ f ( x) $ | ||
| + | satisfying the two following conditions: | ||
| − | + | $$ | |
| + | g ( x) \leq f ( x) ,\ \ | ||
| + | T f ( x) \leq f ( x) , | ||
| + | $$ | ||
| − | where | + | where $ T f ( x) = {\mathsf E} _ {x} g ( x _ {1} ) $. |
| + | Moreover, | ||
| − | + | $$ | |
| + | \tau _ \epsilon = \inf \{ {n \geq 0 } : { | ||
| + | s ( x _ {n} ) \leq g ( x _ {n} ) + \epsilon } \} | ||
| + | $$ | ||
| − | is the | + | is the $ \epsilon $- |
| + | optimal time for any $ \epsilon > 0 $, | ||
| + | the cost $ s ( x) $ | ||
| + | satisfies the Wald–Bellman equation | ||
| − | + | $$ | |
| + | s ( x) = \max \{ g ( x) , T s ( x) \} | ||
| + | $$ | ||
and can be obtained by the formula | and can be obtained by the formula | ||
| − | + | $$ | |
| + | s ( x) = \lim\limits _ {n \rightarrow \infty } Q ^ {n} g ( x) , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | Q g ( x) = \max \{ g ( x) , T g ( x) \} . | ||
| + | $$ | ||
| − | In the case when the set | + | In the case when the set $ E $ |
| + | is finite, the time | ||
| − | + | $$ | |
| + | \tau _ {0} = \inf \{ {n \geq 0 } : {s ( x _ {n} ) = g ( x _ {n} ) } \} | ||
| + | $$ | ||
| − | is optimal. In the general case the time | + | is optimal. In the general case the time $ \tau _ {0} $ |
| + | is optimal if $ {\mathsf P} _ {x} \{ \tau _ {0} < \infty \} = 1 $, | ||
| + | $ x \in E $. | ||
Let | Let | ||
| − | + | $$ | |
| + | C = \{ {X } : {s ( x) > g ( x) } \} | ||
| + | ,\ \ | ||
| + | \Gamma = \{ {x } : {s ( x) = g ( x) } \} | ||
| + | . | ||
| + | $$ | ||
By definition, | By definition, | ||
| − | + | $$ | |
| + | \tau _ {0} = \inf \{ {n \geq 0 } : {x _ {n} \in \Gamma } \} | ||
| + | . | ||
| + | $$ | ||
| − | In other words, one should stop the observations upon hitting the set | + | In other words, one should stop the observations upon hitting the set $ \Gamma $ |
| + | for the first time. Accordingly, the set $ C $ | ||
| + | is called the set of continuation of observations and the set $ \Gamma $ | ||
| + | is called the set of termination of observations. | ||
| − | These results can be illustrated by the problem of deciding between two simple hypotheses, for which Wald has demonstrated the advantage of sequential methods as compared to classical ones. Let the parameter | + | These results can be illustrated by the problem of deciding between two simple hypotheses, for which Wald has demonstrated the advantage of sequential methods as compared to classical ones. Let the parameter $ \theta $ |
| + | take two values 1 and 0 with a priori probabilities $ \pi $ | ||
| + | and $ 1 - \pi $, | ||
| + | respectively, and let the set of termination decisions $ D $ | ||
| + | consist of two points as well: $ d = 1 $( | ||
| + | accept hypothesis $ H _ {1} $: | ||
| + | $ \theta = 1 $) | ||
| + | and $ d = 0 $( | ||
| + | accept hypothesis $ H _ {0} $: | ||
| + | $ \theta = 0 $). | ||
| + | If the function $ W _ {1} ( \theta , d ) $ | ||
| + | is chosen in the form | ||
| − | + | $$ | |
| + | W _ {1} ( \theta , d ) = \ | ||
| + | \left \{ | ||
| + | |||
| + | \begin{array}{ll} | ||
| + | a , & \theta = 1 , d = 0 , \\ | ||
| + | b, & \theta = 0 , d = 1 , \\ | ||
| + | 0 & \textrm{ otherwise , } \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right .$$ | ||
and one puts | and one puts | ||
| − | + | $$ | |
| + | W ( \tau , \theta , d ) = c \tau + | ||
| + | W _ {1} ( \theta , d ) , | ||
| + | $$ | ||
then the expression | then the expression | ||
| − | + | $$ | |
| + | R ^ \delta ( \pi ) = c {\mathsf E} _ \pi \tau + | ||
| + | a \alpha _ \pi ( \delta ) + b \beta _ \pi ( \delta ) | ||
| + | $$ | ||
| − | is obtained for | + | is obtained for $ R ^ \delta ( \pi ) $, |
| + | where | ||
| − | + | $$ | |
| + | \alpha _ \pi ( \delta ) = {\mathsf P} _ \pi \{ d = 0 \mid | ||
| + | \theta = 1 \} ,\ \beta _ \pi ( \delta ) = {\mathsf P} _ \pi \{ d = 1 \mid \theta = 0 \} | ||
| + | $$ | ||
| − | are the error probabilities of the first and second kinds, and | + | are the error probabilities of the first and second kinds, and $ {\mathsf P} _ \pi $ |
| + | denotes the probability distribution in the space of observations corresponding to the a priori distribution $ \pi $. | ||
| + | If $ \pi _ {n} = {\mathsf P} \{ \theta = 1 \mid {\mathcal F} _ {n} \} $ | ||
| + | is the a posteriori probability of the hypothesis $ H _ {1} $: | ||
| + | $ \theta = 1 $ | ||
| + | with respect to the $ \sigma $- | ||
| + | algebra $ {\mathcal F} _ {n} = \sigma \{ \omega : {\xi _ {1} \dots \xi _ {n} } \} $, | ||
| + | then | ||
| − | + | $$ | |
| + | R ^ \delta ( \pi ) = {\mathsf E} _ \pi [ c \tau + g ( \pi _ \tau ) ] , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | g ( \pi ) = \min ( a \pi , b ( 1 - \pi ) ) . | ||
| + | $$ | ||
| − | From the general theory of optimal stopping rules applied to | + | From the general theory of optimal stopping rules applied to $ x _ {n} = ( n , \pi _ {n} ) $ |
| + | it follows that the function $ \rho ( \pi ) = \inf _ \tau R ^ \delta ( \pi ) $ | ||
| + | satisfies the equation | ||
| − | + | $$ | |
| + | \rho ( \pi ) = \min \{ g ( \pi ) , c + T \rho ( \pi ) \} . | ||
| + | $$ | ||
| − | Hence, by virtue of concavity of the functions | + | Hence, by virtue of concavity of the functions $ \rho ( \pi ) $, |
| + | $ g ( \pi ) $, | ||
| + | $ T \rho ( \pi ) $, | ||
| + | it follows that there are two numbers $ 0 \leq A \leq B \leq 1 $ | ||
| + | such that the domain of continuation of observations is $ C = \{ \pi : {A < \pi < B } \} $, | ||
| + | and the domain of termination of observations is $ \Gamma = [ 0 , 1 ] \setminus ( A , B ) $. | ||
| + | Here, the termination time | ||
| − | + | $$ | |
| + | \tau _ {0} = \inf \{ {n \geq 0 } : {\pi _ {n} \in \Gamma } \} | ||
| + | $$ | ||
| − | is optimal | + | is optimal $ ( \pi _ {0} = \pi ) $. |
| − | If | + | If $ p _ {0} ( x) $ |
| + | and $ p _ {1} ( x) $ | ||
| + | are the densities of the distributions $ F _ {0} ( x) $ | ||
| + | and $ F _ {1} ( x) $( | ||
| + | with respect to the measure $ d \mu = ( d F _ {0} + d F _ {1} ) /2 $), | ||
| + | and | ||
| − | + | $$ | |
| + | \phi = | ||
| + | \frac{p _ {1} ( \xi _ {1} ) \dots p _ {1} ( \xi _ {n} ) }{p _ {0} ( \xi _ {1} ) \dots p _ {0} ( \xi _ {n} ) } | ||
| + | |||
| + | $$ | ||
is the likelihood ratio, then the domain of continuation of observations (see Fig. a) can be written in the form | is the likelihood ratio, then the domain of continuation of observations (see Fig. a) can be written in the form | ||
| − | + | $$ | |
| + | C = \left \{ \phi : { | ||
| + | \frac{A}{1-} | ||
| + | A | ||
| + | \frac{1 - \pi } \pi | ||
| + | < \phi | ||
| + | < | ||
| + | \frac{B}{1-} | ||
| + | B | ||
| + | \frac{1 - \pi } \pi | ||
| + | } \right \} | ||
| + | $$ | ||
| − | and | + | and $ \tau _ {0} = \inf \{ {n \geq 0 } : {\phi _ {n} \notin C } \} $. |
| + | $ C $: | ||
| + | domain of continuation of observations $ \Gamma $: | ||
| + | domain of termination of observations | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s084600a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s084600a.gif" /> | ||
| Line 103: | Line 303: | ||
Figure: s084600a | Figure: s084600a | ||
| − | In addition, if | + | In addition, if $ \phi _ {\tau _ {0} } \geq [ B / ( 1 - B ) ] [ ( 1 - \pi ) / \pi ] $, |
| + | then the decision $ d = 1 $ | ||
| + | is taken, i.e. the hypothesis $ H _ {1} $: | ||
| + | $ \theta = 1 $ | ||
| + | is accepted. If, however, $ \phi _ {\tau _ {0} } \leq [ A / ( 1 - A ) ] [ ( 1 - \pi ) / \pi ] $, | ||
| + | then the hypothesis $ H _ {0} $: | ||
| + | $ \theta = 0 $ | ||
| + | is accepted. The structure of this optimal decision rule is the same also for the problem of decision between two hypotheses formulated in terms of a conditional extremum in the following way. For each decision rule $ \delta = ( \tau , d ) $ | ||
| + | one introduces the error probabilities $ \alpha ( \delta ) = {\mathsf P} _ {1} ( d = 0 ) $, | ||
| + | $ \beta ( \delta ) = {\mathsf P} _ {0} ( d = 1 ) $ | ||
| + | and fixes two numbers $ \alpha > 0 $ | ||
| + | and $ \beta > 0 $; | ||
| + | let, further, $ \Delta ( \alpha , \beta ) $ | ||
| + | be the set of all decision rules when $ \alpha ( \delta ) \leq \alpha $, | ||
| + | $ \beta ( \delta ) \leq \beta $, | ||
| + | and $ {\mathsf E} _ {0} \tau < \infty $, | ||
| + | $ {\mathsf E} _ {1} \tau < \infty $. | ||
| + | The following fundamental result was obtained by Wald. If $ \alpha + \beta < 1 $ | ||
| + | and if among all criteria $ \delta = ( \tau , d ) $ | ||
| + | based on the likelihood ratio $ \phi _ {n} $ | ||
| + | and of the form | ||
| + | |||
| + | $$ | ||
| + | \tau = \inf \{ {n \geq 0 } : {\phi _ {n} \notin ( a , b ) } \} | ||
| + | , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | d = \left \{ | ||
| + | \begin{array}{ll} | ||
| + | 1 , &\ | ||
| + | \phi _ \tau \geq b , \\ | ||
| + | 0, & \phi _ \tau \leq a , \\ | ||
| + | \end{array} | ||
| − | + | \right .$$ | |
| − | + | there are $ a = a ^ {*} $ | |
| + | and $ b = b ^ {*} $ | ||
| + | such that the error probabilities of the first and second kinds are exactly $ \alpha $ | ||
| + | and $ \beta $, | ||
| + | then the decision rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $ | ||
| + | with $ a = a ^ {*} $ | ||
| + | and $ b = b ^ {*} $ | ||
| + | is optimal in the class $ \Delta ( \alpha , \beta ) $ | ||
| + | in the sense that | ||
| − | + | $$ | |
| + | {\mathsf E} _ {0} \tau ^ {*} \leq {\mathsf E} _ {0} \tau ,\ \ | ||
| + | {\mathsf E} _ {1} \tau ^ {*} \leq {\mathsf E} _ {1} \tau | ||
| + | $$ | ||
| − | + | for all $ \delta \in \Delta ( \alpha , \beta ) $. | |
| − | + | The advantage of the sequential decision rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $ | |
| + | as compared to the classical one is easier to illustrate by the example of decision between two hypotheses $ H _ {0} $: | ||
| + | $ \theta = 0 $ | ||
| + | and $ H _ {1} $: | ||
| + | $ \theta = 1 $ | ||
| + | with respect to the local average value $ \theta $ | ||
| + | of a Wiener process $ \xi _ {t} $ | ||
| + | with unit diffusion. The optimal sequential decision rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $ | ||
| + | providing the given probabilities $ \alpha $ | ||
| + | and $ \beta $ | ||
| + | of errors of the first and second kinds, respectively, is described as follows: | ||
| − | + | $$ | |
| + | \tau ^ {*} = \inf \{ {t \geq 0 } : {\lambda _ {t} \notin ( a ^ {*} , b ^ {*} ) } \} | ||
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | d ^ {*} = \left \{ | ||
| + | \begin{array}{ll} | ||
| + | 1 , & \lambda _ {\tau ^ {*} } \geq b ^ {*} , \\ | ||
| + | 0, & \lambda _ {\tau ^ {*} } \leq a ^ {*} , \\ | ||
| + | \end{array} | ||
| − | + | \right .$$ | |
| − | where | + | where $ \lambda _ {t} = \mathop{\rm ln} \phi _ {t} $ |
| + | and the likelihood ratio (the density of the measure corresponding to $ \theta = 1 $ | ||
| + | with respect to the measure corresponding to $ \theta = 0 $) | ||
| + | equals $ \phi _ {t} = e ^ {\xi _ {t} - ( t / 2 ) } $, | ||
| + | and $ b ^ {*} = \mathop{\rm ln} ( ( 1 - \alpha ) / \beta ) $, | ||
| + | $ a ^ {*} = \mathop{\rm ln} ( \alpha / ( 1 - \beta ) ) $( | ||
| + | see Fig. b). $ C $: | ||
| + | domain of continuation of observations $ \Gamma $: | ||
| + | domain of termination of observations | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s084600b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s084600b.gif" /> | ||
| Line 127: | Line 397: | ||
Figure: s084600b | Figure: s084600b | ||
| − | The optimal classical rule | + | The optimal classical rule $ \widetilde \delta = ( \widetilde \tau , \widetilde{d} ) $( |
| + | using the Neyman–Pearson lemma) is described in the following way: | ||
| + | |||
| + | $$ | ||
| + | \widetilde{t} = t ( \alpha , \beta ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \widetilde{d} = \left \{ | ||
| + | \begin{array}{ll} | ||
| + | 1 , & \lambda _ {\widetilde{t} } \geq h ( \alpha , \beta ) , \\ | ||
| + | 0, &\ | ||
| + | \lambda _ {\widetilde{t} } < h ( \alpha , \beta ) , \\ | ||
| + | \end{array} | ||
| − | + | \right .$$ | |
where | where | ||
| − | + | $$ | |
| + | t ( \alpha , \beta ) = ( c _ \alpha + c _ \beta ) ^ {2} , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | h ( \alpha , \beta ) = | ||
| + | \frac{c _ \beta ^ {2} - c _ \alpha ^ {2} }{2} | ||
| − | + | $$ | |
| − | and | + | and $ c _ \gamma $ |
| + | is the solution of the equation | ||
| − | + | $$ | |
| − | + | \frac{1}{\sqrt {2 \pi } } | |
| + | \int\limits _ {c _ \gamma } ^ \infty | ||
| + | e ^ {- x ^ {2} / 2 } dx = \gamma . | ||
| + | $$ | ||
| − | + | Since $ {\mathsf E} _ {0} \tau ^ {*} = 2 \omega ( \alpha , \beta ) $, | |
| + | $ {\mathsf E} _ {1} \tau ^ {*} = 2 \omega ( \beta , \alpha ) $, | ||
| + | where | ||
| + | |||
| + | $$ | ||
| + | \omega ( x , y ) = ( 1 - x ) \mathop{\rm ln} \ | ||
| + | 1- | ||
| + | \frac{x}{y} | ||
| + | + x \mathop{\rm ln} | ||
| + | \frac{x}{1-} | ||
| + | y , | ||
| + | $$ | ||
one has | one has | ||
| − | + | $$ | |
| − | + | \frac{ {\mathsf E} _ {0} \tau ^ {*} }{t ( \alpha , \beta ) } | |
| + | = \ | ||
| + | 2 | ||
| + | \frac{\omega ( \beta , \alpha ) }{( c _ \alpha + c _ \beta ) ^ {2} } | ||
| + | ,\ | ||
| + | \frac{ {\mathsf E} _ {1} \tau ^ {*} }{t ( \alpha , \beta) } | ||
| + | = 2 | ||
| − | + | \frac{\omega ( \alpha , \beta ) }{( c _ \alpha + c _ \beta ) ^ {2} } | |
| + | . | ||
| + | $$ | ||
| − | + | Numerical calculations show that for $ \alpha , \beta \leq 0.03 $, | |
| − | + | $$ | |
| + | |||
| + | \frac{ {\mathsf E} _ {0} \tau ^ {*} }{t ( \alpha , \beta ) } | ||
| + | \leq \ | ||
| + | |||
| + | \frac{17}{30} | ||
| + | ,\ | ||
| + | \frac{ {\mathsf E} _ {1} \tau ^ {*} }{t ( \alpha , \beta ) | ||
| + | } | ||
| + | \leq | ||
| + | \frac{17}{30} | ||
| + | . | ||
| + | $$ | ||
| + | |||
| + | In other words, for the values of errors of the first and the second kinds considered, the optimal sequential method of decision between two hypotheses needs approximately half the observations of the optimal method with a fixed number of observations. Moreover, if $ \alpha = \beta $, | ||
| + | then | ||
| + | |||
| + | $$ | ||
| + | \lim\limits _ {\alpha \downarrow 0 } | ||
| + | \frac{ {\mathsf E} _ {0} \tau ^ {*} }{t ( \alpha , \alpha ) } | ||
| + | = \lim\limits _ {\alpha \downarrow 0 } \ | ||
| + | |||
| + | \frac{ {\mathsf E} _ {1} \tau ^ {*} }{t ( \alpha , \alpha ) } | ||
| + | = | ||
| + | \frac{1}{4} | ||
| + | . | ||
| + | $$ | ||
====References==== | ====References==== | ||
| Line 169: | Line 505: | ||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
Latest revision as of 14:55, 7 June 2020
2020 Mathematics Subject Classification: Primary: 62L10 [MSN][ZBL]
A branch of mathematical statistics. Its characteristic feature is that the number of observations to be performed (the moment of termination of the observations) is not fixed in advance but is chosen in the course of the experiment depending upon the results that are obtained. The intensive development and application of sequential methods in statistics was due to the work of A. Wald. He established that in the problem of decision (based on the results of independent observations) between two simple hypotheses the so-called sequential probability ratio test gives a considerable improvement in terms of the average number of observations required in comparison with the most-powerful test for deciding between two hypotheses (determined by the Neyman–Pearson lemma) for a fixed sample size and the same error probabilities.
The basic principles of sequential analysis consist of the following. Let $ \xi _ {1} , \xi _ {2} \dots $ be a sequence of independent identically-distributed random variables with distribution function $ F _ \theta ( x) = {\mathsf P} _ \theta \{ \xi _ {1} \leq x \} $ which depends on an unknown parameter $ \theta $ belonging to some parameter set $ \Theta $. The problem consists of making a certain decision as to the true value of the unknown parameter $ \theta $, based on the results of observations.
A space $ D $ of terminal final decisions $ d $( for the values of the parameter $ \theta $) and a termination rule $ \tau $ which determines the time when the observations are stopped and the terminal decision is taken, lie at the basis of any statistical decision problem. In classical methods the time $ \tau $ is non-random and is fixed in advance; in sequential methods $ \tau $ is a random variable independent of the "future" (a Markovian time, a stopping time). Formally, let $ {\mathcal F} _ {n} = \sigma \{ \omega : {\xi _ {1} \dots \xi _ {n} } \} $ be the $ \sigma $- algebra generated by the random variables $ \xi _ {1} \dots \xi _ {n} $. A random variable $ \tau = \tau ( \omega ) $ assuming the values $ 0 \dots + \infty $ is called a Markovian time if the event $ \{ \tau \leq n \} \in {\mathcal F} _ {n} $ for any $ n \geq 0 $( $ {\mathcal F} _ {0} = \{ \emptyset , \Omega \} $). Let $ {\mathcal F} _ \tau $ be the family of all measurable sets $ A $ such that $ A \cap \{ \tau \leq n \} \in {\mathcal F} _ {n} $ for any $ n \geq 0 $( cf. also Markov moment). If $ {\mathcal F} _ {n} $ is interpreted as the set of events observed up to some random time $ n $( inclusive), then $ {\mathcal F} _ \tau $ can be interpreted as the set of events observed up to the time $ \tau $( inclusive). A terminal decision $ d = d ( \omega ) $ is an $ {\mathcal F} _ \tau $- measurable function with values in $ D $. A pair $ \delta = ( \tau , d ) $ of such functions is called a (sequential) decision rule.
In order to choose the "optimal" decision rule among all decision rules one usually defines a risk function $ W ( \tau , \theta , d ) $ and considers the mathematical expectation $ {\mathsf E} _ \theta W ( \tau , \theta , d ) $. There are different approaches to defining the optimal decision rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $. One of them, the Bayesian approach, is based on the assumption that the parameter $ \theta $ is a random variable with a priori distribution $ \pi = \pi ( d \theta ) $. Then one can speak of the $ \pi $- risk
$$ R ^ \delta ( \pi ) = \int\limits _ \Theta {\mathsf E} _ \theta W ( \tau , \theta , d ) \pi ( d \theta ) $$
and one calls a rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $ the optimal Bayesian (or $ \pi $- optimal) solution if $ R ^ {\delta * } ( \pi ) \leq R ^ \delta ( \pi ) $ for any other (admissible) rule. The most widely used form of the risk function $ W ( \tau , \theta , d ) $ is $ c \tau + W _ {1} ( \theta , d ) $, where the constant $ c \geq 0 $ is interpreted as the cost of a unit observation and $ W _ {1} ( \theta , d ) $ is a loss function resulting from the terminal decision.
In Bayesian problems it is usually not difficult to find the terminal solution $ d ^ {*} $; thus the main efforts are concentrated on finding the optimal termination time $ \tau ^ {*} $. Moreover, the majority of problems of sequential analysis fall into the following pattern of "optimal termination rules" .
Let $ X = ( x _ {n} , {\mathcal F} _ {n} , {\mathsf P} _ {x} ) $, $ n \geq 0 $, $ x \in E $, be a Markov chain in the state space $ ( E , {\mathcal B} ) $, where $ x _ {n} $ is the state of the chain at the time $ n $, the $ \sigma $- algebra $ {\mathcal F} _ {n} $ is interpreted as the set of events observed up to the time $ n $( inclusive), and $ {\mathsf P} _ {x} $ is a probability distribution corresponding to the initial state $ x \in E $. It is assumed that by stopping the observation at the time $ n $ one obtains the gain $ g ( x _ {n} ) $. Then the average gain resulting from termination at time $ \tau $ is $ {\mathsf E} _ {x} g ( x _ \tau ) $, where $ x $ is the initial state. The function $ s ( x) = \sup {\mathsf E} _ {x} g ( x _ \tau ) $, where the supremum is taken over all (finite) termination times $ \tau $, is called the cost, and the time $ \tau _ \epsilon $ for which $ s ( x) \leq {\mathsf E} g ( x _ \tau ) + \epsilon $ for all $ x \in E $ is called the $ \epsilon $- optimal stopping time. $ 0 $- optimal times are called optimal. The main problems in the theory of "optimal stopping rules" are the following: What is the structure of the cost $ s ( x) $, how to find it, when do $ \epsilon $- optimal and optimal times exist, and what is their structure? One of the typical results concerning these questions is discussed below.
Let the function $ g ( x) $ be bounded: $ | g ( x) | \leq c < \infty $. Then the cost $ s ( x) $ is the least excessive majorant of $ g ( x) $, i.e. the smallest of the functions $ f ( x) $ satisfying the two following conditions:
$$ g ( x) \leq f ( x) ,\ \ T f ( x) \leq f ( x) , $$
where $ T f ( x) = {\mathsf E} _ {x} g ( x _ {1} ) $. Moreover,
$$ \tau _ \epsilon = \inf \{ {n \geq 0 } : { s ( x _ {n} ) \leq g ( x _ {n} ) + \epsilon } \} $$
is the $ \epsilon $- optimal time for any $ \epsilon > 0 $, the cost $ s ( x) $ satisfies the Wald–Bellman equation
$$ s ( x) = \max \{ g ( x) , T s ( x) \} $$
and can be obtained by the formula
$$ s ( x) = \lim\limits _ {n \rightarrow \infty } Q ^ {n} g ( x) , $$
where
$$ Q g ( x) = \max \{ g ( x) , T g ( x) \} . $$
In the case when the set $ E $ is finite, the time
$$ \tau _ {0} = \inf \{ {n \geq 0 } : {s ( x _ {n} ) = g ( x _ {n} ) } \} $$
is optimal. In the general case the time $ \tau _ {0} $ is optimal if $ {\mathsf P} _ {x} \{ \tau _ {0} < \infty \} = 1 $, $ x \in E $.
Let
$$ C = \{ {X } : {s ( x) > g ( x) } \} ,\ \ \Gamma = \{ {x } : {s ( x) = g ( x) } \} . $$
By definition,
$$ \tau _ {0} = \inf \{ {n \geq 0 } : {x _ {n} \in \Gamma } \} . $$
In other words, one should stop the observations upon hitting the set $ \Gamma $ for the first time. Accordingly, the set $ C $ is called the set of continuation of observations and the set $ \Gamma $ is called the set of termination of observations.
These results can be illustrated by the problem of deciding between two simple hypotheses, for which Wald has demonstrated the advantage of sequential methods as compared to classical ones. Let the parameter $ \theta $ take two values 1 and 0 with a priori probabilities $ \pi $ and $ 1 - \pi $, respectively, and let the set of termination decisions $ D $ consist of two points as well: $ d = 1 $( accept hypothesis $ H _ {1} $: $ \theta = 1 $) and $ d = 0 $( accept hypothesis $ H _ {0} $: $ \theta = 0 $). If the function $ W _ {1} ( \theta , d ) $ is chosen in the form
$$ W _ {1} ( \theta , d ) = \ \left \{ \begin{array}{ll} a , & \theta = 1 , d = 0 , \\ b, & \theta = 0 , d = 1 , \\ 0 & \textrm{ otherwise , } \\ \end{array} \right .$$
and one puts
$$ W ( \tau , \theta , d ) = c \tau + W _ {1} ( \theta , d ) , $$
then the expression
$$ R ^ \delta ( \pi ) = c {\mathsf E} _ \pi \tau + a \alpha _ \pi ( \delta ) + b \beta _ \pi ( \delta ) $$
is obtained for $ R ^ \delta ( \pi ) $, where
$$ \alpha _ \pi ( \delta ) = {\mathsf P} _ \pi \{ d = 0 \mid \theta = 1 \} ,\ \beta _ \pi ( \delta ) = {\mathsf P} _ \pi \{ d = 1 \mid \theta = 0 \} $$
are the error probabilities of the first and second kinds, and $ {\mathsf P} _ \pi $ denotes the probability distribution in the space of observations corresponding to the a priori distribution $ \pi $. If $ \pi _ {n} = {\mathsf P} \{ \theta = 1 \mid {\mathcal F} _ {n} \} $ is the a posteriori probability of the hypothesis $ H _ {1} $: $ \theta = 1 $ with respect to the $ \sigma $- algebra $ {\mathcal F} _ {n} = \sigma \{ \omega : {\xi _ {1} \dots \xi _ {n} } \} $, then
$$ R ^ \delta ( \pi ) = {\mathsf E} _ \pi [ c \tau + g ( \pi _ \tau ) ] , $$
where
$$ g ( \pi ) = \min ( a \pi , b ( 1 - \pi ) ) . $$
From the general theory of optimal stopping rules applied to $ x _ {n} = ( n , \pi _ {n} ) $ it follows that the function $ \rho ( \pi ) = \inf _ \tau R ^ \delta ( \pi ) $ satisfies the equation
$$ \rho ( \pi ) = \min \{ g ( \pi ) , c + T \rho ( \pi ) \} . $$
Hence, by virtue of concavity of the functions $ \rho ( \pi ) $, $ g ( \pi ) $, $ T \rho ( \pi ) $, it follows that there are two numbers $ 0 \leq A \leq B \leq 1 $ such that the domain of continuation of observations is $ C = \{ \pi : {A < \pi < B } \} $, and the domain of termination of observations is $ \Gamma = [ 0 , 1 ] \setminus ( A , B ) $. Here, the termination time
$$ \tau _ {0} = \inf \{ {n \geq 0 } : {\pi _ {n} \in \Gamma } \} $$
is optimal $ ( \pi _ {0} = \pi ) $.
If $ p _ {0} ( x) $ and $ p _ {1} ( x) $ are the densities of the distributions $ F _ {0} ( x) $ and $ F _ {1} ( x) $( with respect to the measure $ d \mu = ( d F _ {0} + d F _ {1} ) /2 $), and
$$ \phi = \frac{p _ {1} ( \xi _ {1} ) \dots p _ {1} ( \xi _ {n} ) }{p _ {0} ( \xi _ {1} ) \dots p _ {0} ( \xi _ {n} ) } $$
is the likelihood ratio, then the domain of continuation of observations (see Fig. a) can be written in the form
$$ C = \left \{ \phi : { \frac{A}{1-} A \frac{1 - \pi } \pi < \phi < \frac{B}{1-} B \frac{1 - \pi } \pi } \right \} $$
and $ \tau _ {0} = \inf \{ {n \geq 0 } : {\phi _ {n} \notin C } \} $. $ C $: domain of continuation of observations $ \Gamma $: domain of termination of observations
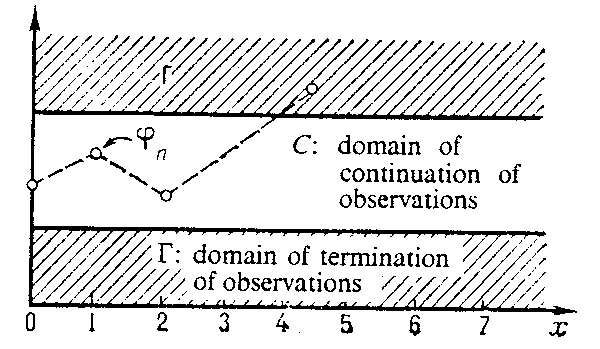
Figure: s084600a
In addition, if $ \phi _ {\tau _ {0} } \geq [ B / ( 1 - B ) ] [ ( 1 - \pi ) / \pi ] $, then the decision $ d = 1 $ is taken, i.e. the hypothesis $ H _ {1} $: $ \theta = 1 $ is accepted. If, however, $ \phi _ {\tau _ {0} } \leq [ A / ( 1 - A ) ] [ ( 1 - \pi ) / \pi ] $, then the hypothesis $ H _ {0} $: $ \theta = 0 $ is accepted. The structure of this optimal decision rule is the same also for the problem of decision between two hypotheses formulated in terms of a conditional extremum in the following way. For each decision rule $ \delta = ( \tau , d ) $ one introduces the error probabilities $ \alpha ( \delta ) = {\mathsf P} _ {1} ( d = 0 ) $, $ \beta ( \delta ) = {\mathsf P} _ {0} ( d = 1 ) $ and fixes two numbers $ \alpha > 0 $ and $ \beta > 0 $; let, further, $ \Delta ( \alpha , \beta ) $ be the set of all decision rules when $ \alpha ( \delta ) \leq \alpha $, $ \beta ( \delta ) \leq \beta $, and $ {\mathsf E} _ {0} \tau < \infty $, $ {\mathsf E} _ {1} \tau < \infty $. The following fundamental result was obtained by Wald. If $ \alpha + \beta < 1 $ and if among all criteria $ \delta = ( \tau , d ) $ based on the likelihood ratio $ \phi _ {n} $ and of the form
$$ \tau = \inf \{ {n \geq 0 } : {\phi _ {n} \notin ( a , b ) } \} , $$
$$ d = \left \{ \begin{array}{ll} 1 , &\ \phi _ \tau \geq b , \\ 0, & \phi _ \tau \leq a , \\ \end{array} \right .$$
there are $ a = a ^ {*} $ and $ b = b ^ {*} $ such that the error probabilities of the first and second kinds are exactly $ \alpha $ and $ \beta $, then the decision rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $ with $ a = a ^ {*} $ and $ b = b ^ {*} $ is optimal in the class $ \Delta ( \alpha , \beta ) $ in the sense that
$$ {\mathsf E} _ {0} \tau ^ {*} \leq {\mathsf E} _ {0} \tau ,\ \ {\mathsf E} _ {1} \tau ^ {*} \leq {\mathsf E} _ {1} \tau $$
for all $ \delta \in \Delta ( \alpha , \beta ) $.
The advantage of the sequential decision rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $ as compared to the classical one is easier to illustrate by the example of decision between two hypotheses $ H _ {0} $: $ \theta = 0 $ and $ H _ {1} $: $ \theta = 1 $ with respect to the local average value $ \theta $ of a Wiener process $ \xi _ {t} $ with unit diffusion. The optimal sequential decision rule $ \delta ^ {*} = ( \tau ^ {*} , d ^ {*} ) $ providing the given probabilities $ \alpha $ and $ \beta $ of errors of the first and second kinds, respectively, is described as follows:
$$ \tau ^ {*} = \inf \{ {t \geq 0 } : {\lambda _ {t} \notin ( a ^ {*} , b ^ {*} ) } \} , $$
$$ d ^ {*} = \left \{ \begin{array}{ll} 1 , & \lambda _ {\tau ^ {*} } \geq b ^ {*} , \\ 0, & \lambda _ {\tau ^ {*} } \leq a ^ {*} , \\ \end{array} \right .$$
where $ \lambda _ {t} = \mathop{\rm ln} \phi _ {t} $ and the likelihood ratio (the density of the measure corresponding to $ \theta = 1 $ with respect to the measure corresponding to $ \theta = 0 $) equals $ \phi _ {t} = e ^ {\xi _ {t} - ( t / 2 ) } $, and $ b ^ {*} = \mathop{\rm ln} ( ( 1 - \alpha ) / \beta ) $, $ a ^ {*} = \mathop{\rm ln} ( \alpha / ( 1 - \beta ) ) $( see Fig. b). $ C $: domain of continuation of observations $ \Gamma $: domain of termination of observations
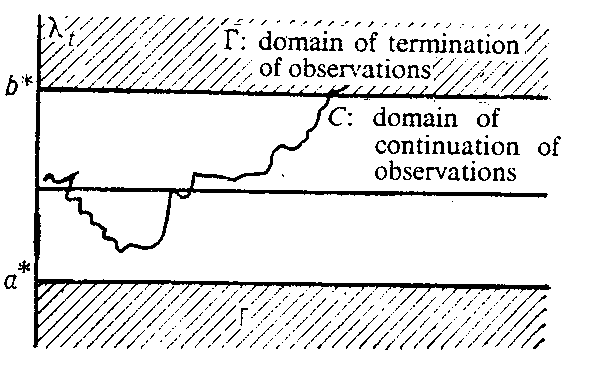
Figure: s084600b
The optimal classical rule $ \widetilde \delta = ( \widetilde \tau , \widetilde{d} ) $( using the Neyman–Pearson lemma) is described in the following way:
$$ \widetilde{t} = t ( \alpha , \beta ) , $$
$$ \widetilde{d} = \left \{ \begin{array}{ll} 1 , & \lambda _ {\widetilde{t} } \geq h ( \alpha , \beta ) , \\ 0, &\ \lambda _ {\widetilde{t} } < h ( \alpha , \beta ) , \\ \end{array} \right .$$
where
$$ t ( \alpha , \beta ) = ( c _ \alpha + c _ \beta ) ^ {2} , $$
$$ h ( \alpha , \beta ) = \frac{c _ \beta ^ {2} - c _ \alpha ^ {2} }{2} $$
and $ c _ \gamma $ is the solution of the equation
$$ \frac{1}{\sqrt {2 \pi } } \int\limits _ {c _ \gamma } ^ \infty e ^ {- x ^ {2} / 2 } dx = \gamma . $$
Since $ {\mathsf E} _ {0} \tau ^ {*} = 2 \omega ( \alpha , \beta ) $, $ {\mathsf E} _ {1} \tau ^ {*} = 2 \omega ( \beta , \alpha ) $, where
$$ \omega ( x , y ) = ( 1 - x ) \mathop{\rm ln} \ 1- \frac{x}{y} + x \mathop{\rm ln} \frac{x}{1-} y , $$
one has
$$ \frac{ {\mathsf E} _ {0} \tau ^ {*} }{t ( \alpha , \beta ) } = \ 2 \frac{\omega ( \beta , \alpha ) }{( c _ \alpha + c _ \beta ) ^ {2} } ,\ \frac{ {\mathsf E} _ {1} \tau ^ {*} }{t ( \alpha , \beta) } = 2 \frac{\omega ( \alpha , \beta ) }{( c _ \alpha + c _ \beta ) ^ {2} } . $$
Numerical calculations show that for $ \alpha , \beta \leq 0.03 $,
$$ \frac{ {\mathsf E} _ {0} \tau ^ {*} }{t ( \alpha , \beta ) } \leq \ \frac{17}{30} ,\ \frac{ {\mathsf E} _ {1} \tau ^ {*} }{t ( \alpha , \beta ) } \leq \frac{17}{30} . $$
In other words, for the values of errors of the first and the second kinds considered, the optimal sequential method of decision between two hypotheses needs approximately half the observations of the optimal method with a fixed number of observations. Moreover, if $ \alpha = \beta $, then
$$ \lim\limits _ {\alpha \downarrow 0 } \frac{ {\mathsf E} _ {0} \tau ^ {*} }{t ( \alpha , \alpha ) } = \lim\limits _ {\alpha \downarrow 0 } \ \frac{ {\mathsf E} _ {1} \tau ^ {*} }{t ( \alpha , \alpha ) } = \frac{1}{4} . $$
References
| [W] | A. Wald, "Sequential analysis" , Wiley (1947) MR0020764 Zbl 0041.26303 Zbl 0029.15805 |
| [Sh] | A.N. Shiryaev, "Statistical sequential analysis" , Amer. Math. Soc. (1973) (Translated from Russian) MR0445744 MR0293789 Zbl 0267.62039 |
| [Sh2] | A.N. Shiryaev, "Optimal stopping rules" , Springer (1978) (Translated from Russian) MR2374974 MR1317981 MR0445744 MR0293789 MR0283922 Zbl 0391.60002 |
Comments
References
| [Si] | D. Siegmund, "Sequential analysis" , Springer (1985) MR0799155 Zbl 0573.62071 |
| [L] | R. Lerche, "Boundary crossing of Brownian motion: its relation to the law of the iterated logarithm and to sequential analysis" , Springer (1986) Zbl 0604.62075 |
Sequential analysis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sequential_analysis&oldid=49580