Difference between revisions of "Riemann hypothesis, generalized"
Ulf Rehmann (talk | contribs) m (Undo revision 48548 by Ulf Rehmann (talk)) Tag: Undo |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | r0819401.png | ||
| + | $#A+1 = 43 n = 1 | ||
| + | $#C+1 = 43 : ~/encyclopedia/old_files/data/R081/R.0801940 Riemann hypothesis, generalized | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | A statement about the non-trivial zeros of Dirichlet $ L $- | ||
| + | functions (cf. [[Dirichlet L-function|Dirichlet $ L $- | ||
| + | function]]), Dedekind zeta-functions (cf. [[Zeta-function|Zeta-function]]) and several other similar functions, similar to the Riemann hypothesis (cf. [[Riemann hypotheses|Riemann hypotheses]]) on the non-trivial zeros of the Riemann zeta-function $ \zeta ( s) $. | ||
| + | In the case of Dirichlet zeta-functions the generalized Riemann hypothesis is called the extended Riemann hypothesis. | ||
====Comments==== | ====Comments==== | ||
| − | For Dirichlet | + | For Dirichlet $ L $- |
| + | functions it is not even known whether there exist real zeros in the interval $ [ 0, 1] $( | ||
| + | Siegel zeros). This is important in connection with the class number of quadratic fields (see also [[Quadratic field|Quadratic field]]; [[Siegel theorem|Siegel theorem]]). | ||
| − | Let | + | Let $ K $ |
| + | be an algebraic number field, $ G( K) $ | ||
| + | the group of fractional ideals of $ K $ | ||
| + | and $ C( K) $ | ||
| + | its idèle class group (cf. [[Idèle|Idèle]]; [[Fractional ideal|Fractional ideal]]). Let $ X $ | ||
| + | be a quasi-character on $ C( K) $, | ||
| + | i.e. a continuous homomorphism of $ C( K) $ | ||
| + | into the group of non-zero complex numbers. Then for an idèle $ ( x _ {v} ) $ | ||
| + | one has $ X ( ( x _ {v} ) ) = \prod _ {v} X _ {v} ( x _ {v} ) $, | ||
| + | where for each $ v $, | ||
| + | $ X _ {v} $ | ||
| + | is a quasi-character of $ K _ {v} ^ {*} $ | ||
| + | which is equal to unity on $ U( K _ {v} ) $, | ||
| + | the units of the local completion $ K _ {v} $, | ||
| + | for almost-all $ v $. | ||
| + | Let $ S $ | ||
| + | be a finite subset of the valuations on $ K $ | ||
| + | including the Archimedian ones, $ S _ \infty $. | ||
| + | A function $ \chi $ | ||
| + | can now be defined on $ G( K) $ | ||
| + | by setting for all prime ideals $ \mathfrak P $, | ||
| − | + | $$ | |
| + | \chi ( \mathfrak P ) = \left \{ | ||
| − | + | \begin{array}{cl} | |
| + | {X _ {v} ( \mathfrak p v) } & {\textrm{ if } \mathfrak P = \mathfrak p _ {v} , v \notin S, } \\ | ||
| + | 0 & {\textrm{ otherwise } , } \\ | ||
| + | \end{array} | ||
| + | \right . | ||
| + | $$ | ||
| − | + | and extending $ \chi $ | |
| + | multiplicatively. These functions are called Hecke characters or Grössencharakters. Given such a character, the Hecke zeta-function of $ \chi $ | ||
| + | is defined by | ||
| − | + | $$ | |
| + | \zeta ( s , \chi ) = \prod _ { \mathfrak p } | ||
| + | \left ( 1 - | ||
| + | \frac{\chi ( \mathfrak p ) }{N( \mathfrak p ) ^ {s} } | ||
| + | |||
| + | \right ) ^ {-} 1 = \ | ||
| + | \sum _ { \mathfrak a } | ||
| + | |||
| + | \frac{\chi ( \mathfrak a ) }{N( \mathfrak a ) ^ {s} } | ||
| + | , | ||
| + | $$ | ||
| + | |||
| + | where $ N $ | ||
| + | is the absolute norm $ G( K) \rightarrow G( \mathbf Q ) $. | ||
| + | The function $ \zeta ( s, \chi ) $ | ||
| + | is also called $ L $- | ||
| + | series, Dirichlet $ L $- | ||
| + | series (when $ \chi $ | ||
| + | is a Dirichlet character) or Hecke $ L $- | ||
| + | function with Grössencharakter; it is also denoted by $ L( s, \chi ) $. | ||
| + | If $ \chi \equiv 1 $ | ||
| + | one obtains the Dedekind $ \zeta $- | ||
| + | function. For Dirichlet $ L $- | ||
| + | series the generalized Riemann hypothesis states that $ L ( s, \chi ) \neq 0 $ | ||
| + | if $ \mathop{\rm Re} ( s) > 1/2 $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Heilbronn, "Zeta-functions and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194049.png" />-functions" J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' , Acad. Press (1967) pp. 204–230</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , Springer & PWN (1990) pp. Chapt. 7, §1</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Heilbronn, "Zeta-functions and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194049.png" />-functions" J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' , Acad. Press (1967) pp. 204–230</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , Springer & PWN (1990) pp. Chapt. 7, §1</TD></TR></table> | ||
Revision as of 14:55, 7 June 2020
A statement about the non-trivial zeros of Dirichlet $ L $-
functions (cf. Dirichlet $ L $-
function), Dedekind zeta-functions (cf. Zeta-function) and several other similar functions, similar to the Riemann hypothesis (cf. Riemann hypotheses) on the non-trivial zeros of the Riemann zeta-function $ \zeta ( s) $.
In the case of Dirichlet zeta-functions the generalized Riemann hypothesis is called the extended Riemann hypothesis.
Comments
For Dirichlet $ L $- functions it is not even known whether there exist real zeros in the interval $ [ 0, 1] $( Siegel zeros). This is important in connection with the class number of quadratic fields (see also Quadratic field; Siegel theorem).
Let $ K $ be an algebraic number field, $ G( K) $ the group of fractional ideals of $ K $ and $ C( K) $ its idèle class group (cf. Idèle; Fractional ideal). Let $ X $ be a quasi-character on $ C( K) $, i.e. a continuous homomorphism of $ C( K) $ into the group of non-zero complex numbers. Then for an idèle $ ( x _ {v} ) $ one has $ X ( ( x _ {v} ) ) = \prod _ {v} X _ {v} ( x _ {v} ) $, where for each $ v $, $ X _ {v} $ is a quasi-character of $ K _ {v} ^ {*} $ which is equal to unity on $ U( K _ {v} ) $, the units of the local completion $ K _ {v} $, for almost-all $ v $. Let $ S $ be a finite subset of the valuations on $ K $ including the Archimedian ones, $ S _ \infty $. A function $ \chi $ can now be defined on $ G( K) $ by setting for all prime ideals $ \mathfrak P $,
$$ \chi ( \mathfrak P ) = \left \{ \begin{array}{cl} {X _ {v} ( \mathfrak p v) } & {\textrm{ if } \mathfrak P = \mathfrak p _ {v} , v \notin S, } \\ 0 & {\textrm{ otherwise } , } \\ \end{array} \right . $$
and extending $ \chi $ multiplicatively. These functions are called Hecke characters or Grössencharakters. Given such a character, the Hecke zeta-function of $ \chi $ is defined by
$$ \zeta ( s , \chi ) = \prod _ { \mathfrak p } \left ( 1 - \frac{\chi ( \mathfrak p ) }{N( \mathfrak p ) ^ {s} } \right ) ^ {-} 1 = \ \sum _ { \mathfrak a } \frac{\chi ( \mathfrak a ) }{N( \mathfrak a ) ^ {s} } , $$
where $ N $ is the absolute norm $ G( K) \rightarrow G( \mathbf Q ) $. The function $ \zeta ( s, \chi ) $ is also called $ L $- series, Dirichlet $ L $- series (when $ \chi $ is a Dirichlet character) or Hecke $ L $- function with Grössencharakter; it is also denoted by $ L( s, \chi ) $. If $ \chi \equiv 1 $ one obtains the Dedekind $ \zeta $- function. For Dirichlet $ L $- series the generalized Riemann hypothesis states that $ L ( s, \chi ) \neq 0 $ if $ \mathop{\rm Re} ( s) > 1/2 $.
References
| [a1] | H. Heilbronn, "Zeta-functions and 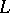 -functions" J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) pp. 204–230 -functions" J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) pp. 204–230 |
| [a2] | W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , Springer & PWN (1990) pp. Chapt. 7, §1 |
Riemann hypothesis, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_hypothesis,_generalized&oldid=49562