Namespaces
Variants
Actions

Difference between revisions of "Rectifying plane"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48452 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
The plane of the Frénet frame (cf. [[Frénet trihedron|Frénet trihedron]]) of a given point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080140/r0801401.png" /> on a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080140/r0801402.png" /> (cf. [[Line (curve)|Line (curve)]]) which is spanned by the tangent (cf. [[Tangent line|Tangent line]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080140/r0801403.png" /> and the [[Binormal|binormal]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080140/r0801404.png" /> to the curve at this point. The equation of the rectifying plane can be written in the form
−
r0801401.png
 
−
$#A+1 = 7 n = 0
 
−
$#C+1 = 7 : ~/encyclopedia/old_files/data/R080/R.0800140 Rectifying plane
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080140/r0801405.png" /></td> </tr></table>
−
{{TEX|done}}
 
  
−
The plane of the Frénet frame (cf. [[Frénet trihedron|Frénet trihedron]]) of a given point  $  A $
+
or
−
on a curve  $  \mathbf r = \mathbf r ( t) $(
 
−
cf. [[Line (curve)|Line (curve)]]) which is spanned by the tangent (cf. [[Tangent line|Tangent line]])  $  \mathbf t $
 
−
and the [[Binormal|binormal]]  $  \mathbf b $
 
−
to the curve at this point. The equation of the rectifying plane can be written in the form
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080140/r0801406.png" /></td> </tr></table>
−
\left |
 
  
−
or
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080140/r0801407.png" /> is the equation of the curve.
  
−
$$
 
−
( \mathbf R - \mathbf r ) \mathbf r  ^  \prime  [ \mathbf r  ^  \prime  , \mathbf r
 
−
^ {\prime\prime} ]  =  0,
 
−
$$
 
  
−
where  $  \mathbf r ( t) = \mathbf r ( x( t), y( t), z( t)) $
 
−
is the equation of the curve.
 
  
 
====Comments====
 
====Comments====
 +
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  M. Spivak,  "A comprehensive introduction to differential geometry" , '''2''' , Publish or Perish  (1970)  pp. 1–5</TD></TR></table>
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  M. Spivak,  "A comprehensive introduction to differential geometry" , '''2''' , Publish or Perish  (1970)  pp. 1–5</TD></TR></table>

Revision as of 14:53, 7 June 2020

The plane of the Frénet frame (cf. Frénet trihedron) of a given point 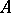on a curve 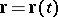(cf. Line (curve)) which is spanned by the tangent (cf. Tangent line) 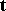and the binormal 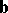to the curve at this point. The equation of the rectifying plane can be written in the form

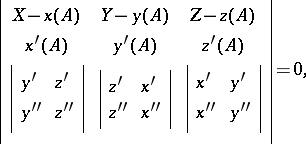or

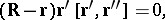where 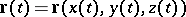is the equation of the curve.


Comments

References

[a1] M. Spivak, "A comprehensive introduction to differential geometry" , 2 , Publish or Perish (1970) pp. 1–5
How to Cite This Entry:
Rectifying plane. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rectifying_plane&oldid=49393
This article was adapted from an original article by L.A. Sidorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Rectifying_plane&oldid=49393"