Difference between revisions of "Norm on a field"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48006 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n0673601.png" />'' |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n0673602.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n0673603.png" /> to the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n0673604.png" /> of real numbers, which satisfies the following conditions: | |
| − | |||
| − | + | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n0673605.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n0673606.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n0673607.png" />; | |
| − | + | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n0673608.png" />; | |
| − | |||
| − | |||
| − | |||
| − | + | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n0673609.png" />. | |
| − | |||
| − | |||
| − | + | Hence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736010.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736011.png" />. | |
| − | + | The norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736012.png" /> is often denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736013.png" /> instead of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736014.png" />. A norm is also called an absolute value or a multiplicative valuation. Norms may (more generally) be considered on any ring with values in a linearly ordered ring [[#References|[4]]]. See also [[Valuation|Valuation]]. | |
| − | + | Examples of norms. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736015.png" />, the field of real numbers, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736016.png" />, the ordinary [[Absolute value|absolute value]] or modulus of the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736017.png" />, is a norm. Similarly, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736018.png" /> is the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736019.png" /> of complex numbers or the skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736020.png" /> of quaternions, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736021.png" /> is a norm. The subfields of these fields are thus also provided with an induced norm. Any field has the trivial norm: | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736022.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Finite fields and their algebraic extensions only have the trivial norm. | Finite fields and their algebraic extensions only have the trivial norm. | ||
| − | Examples of norms of another type are provided by logarithmic valuations of a field | + | Examples of norms of another type are provided by logarithmic valuations of a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736023.png" />: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736024.png" /> is a valuation on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736025.png" /> with values in the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736026.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736027.png" /> is a real number, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736028.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736029.png" /> is a norm. For example, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736031.png" /> is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736032.png" />-adic valuation of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736033.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736034.png" /> is called the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736036.png" />-adic absolute value or the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736038.png" />-adic norm. These absolute values satisfy the following condition, which is stronger than 3): |
| − | If | ||
| − | is a valuation on | ||
| − | with values in the group | ||
| − | and if | ||
| − | is a real number, | ||
| − | then | ||
| − | is a norm. For example, if | ||
| − | and | ||
| − | is the | ||
| − | adic valuation of the field | ||
| − | then | ||
| − | is called the | ||
| − | adic absolute value or the | ||
| − | adic norm. These absolute values satisfy the following condition, which is stronger than 3): | ||
| − | 4) | + | 4) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736039.png" />. |
| − | Norms satisfying condition 4) are known as ultra-metric norms or non-Archimedean norms (as distinct from Archimedean norms which do not satisfy this condition (but do satisfy 3)). They are distinguished by the fact that | + | Norms satisfying condition 4) are known as ultra-metric norms or non-Archimedean norms (as distinct from Archimedean norms which do not satisfy this condition (but do satisfy 3)). They are distinguished by the fact that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736040.png" /> for all integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736041.png" />. All norms on a field of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736042.png" /> are ultra-metric. All ultra-metric norms are obtained from valuations as indicated above: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736043.png" /> (and conversely, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736044.png" /> can always be taken as a valuation). |
| − | for all integers | ||
| − | All norms on a field of characteristic | ||
| − | are ultra-metric. All ultra-metric norms are obtained from valuations as indicated above: | ||
| − | and conversely, | ||
| − | can always be taken as a valuation). | ||
| − | A norm | + | A norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736045.png" /> defines a [[Metric|metric]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736046.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736047.png" /> is taken as the distance between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736048.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736049.png" />, and in this way it defines a topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736050.png" />. The topology of any locally compact field is defined by some norm. Two norms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736051.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736052.png" /> are said to be equivalent if they define the same topology; in a such case there exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736053.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736054.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736055.png" />. |
| − | defines a [[Metric|metric]] on | ||
| − | if | ||
| − | is taken as the distance between | ||
| − | and | ||
| − | and in this way it defines a topology on | ||
| − | The topology of any locally compact field is defined by some norm. Two norms | ||
| − | and | ||
| − | are said to be equivalent if they define the same topology; in a such case there exists a | ||
| − | such that | ||
| − | for all | ||
| − | The structure of all Archimedean norms is given by Ostrowski's theorem: If | + | The structure of all Archimedean norms is given by Ostrowski's theorem: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736056.png" /> is an Archimedean norm on a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736057.png" />, then there exists an isomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736058.png" /> into a certain everywhere-dense subfield of one of the fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736060.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736061.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736062.png" /> is equivalent to the norm induced by that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736063.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736064.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736065.png" />. |
| − | is an Archimedean norm on a field | ||
| − | then there exists an isomorphism of | ||
| − | into a certain everywhere-dense subfield of one of the fields | ||
| − | |||
| − | or | ||
| − | such that | ||
| − | is equivalent to the norm induced by that of | ||
| − | |||
| − | or | ||
| − | Any non-trivial norm of the field | + | Any non-trivial norm of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736066.png" /> of rational numbers is equivalent either to a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736067.png" />-adic norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736068.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736069.png" /> is a prime number, or to the ordinary norm. For any rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736070.png" /> one has |
| − | of rational numbers is equivalent either to a | ||
| − | adic norm | ||
| − | where | ||
| − | is a prime number, or to the ordinary norm. For any rational number | ||
| − | one has | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736071.png" /></td> </tr></table> | |
| − | |||
| − | |||
A similar formula is also valid for algebraic number fields [[#References|[2]]], [[#References|[3]]]. | A similar formula is also valid for algebraic number fields [[#References|[2]]], [[#References|[3]]]. | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736072.png" /> is a norm on a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736073.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736074.png" /> may be imbedded by the classical completion process in a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736075.png" /> that is complete with respect to the norm that (uniquely) extends <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736076.png" /> (cf. [[Complete topological space|Complete topological space]]). One of the principal modern methods in the study of fields is the imbedding of a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736077.png" /> into the direct product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736078.png" /> of all completions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736079.png" /> of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736080.png" /> with respect to all non-trivial norms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736081.png" /> (see [[Adèle|Adèle]]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736082.png" /> admits non-trivial valuations, then it is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736083.png" /> in the adèlic topology; in fact, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736084.png" /> are non-trivial, non-equivalent norms on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736085.png" />, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736086.png" /> are elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736087.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736088.png" />, then there exists an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736089.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736090.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736091.png" /> (the approximation theorem for norms). |
| − | is a norm on a field | ||
| − | then | ||
| − | may be imbedded by the classical completion process in a field | ||
| − | that is complete with respect to the norm that (uniquely) extends | ||
| − | cf. [[Complete topological space|Complete topological space]]). One of the principal modern methods in the study of fields is the imbedding of a field | ||
| − | into the direct product | ||
| − | of all completions | ||
| − | of the field | ||
| − | with respect to all non-trivial norms of | ||
| − | see [[Adèle|Adèle]]). If | ||
| − | admits non-trivial valuations, then it is dense in | ||
| − | in the adèlic topology; in fact, if | ||
| − | are non-trivial, non-equivalent norms on | ||
| − | if | ||
| − | are elements of | ||
| − | and if | ||
| − | then there exists an | ||
| − | such that | ||
| − | for all | ||
| − | the approximation theorem for norms). | ||
| − | A norm on a field | + | A norm on a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736092.png" /> may be extended (in general, non-uniquely) to any algebraic field extension of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736093.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736094.png" /> is complete with respect to the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736095.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736096.png" /> is an extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736097.png" /> of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736098.png" />, the extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n06736099.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n067360100.png" /> is unique, and is given by the formula |
| − | may be extended (in general, non-uniquely) to any algebraic field extension of the field | ||
| − | If | ||
| − | is complete with respect to the norm | ||
| − | and if | ||
| − | is an extension of | ||
| − | of degree | ||
| − | the extension of | ||
| − | to | ||
| − | is unique, and is given by the formula | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n067360101.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | for | + | for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n067360102.png" />. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lang, "Algebra" , Addison-Wesley (1984)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' , Acad. Press (1986)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lang, "Algebra" , Addison-Wesley (1984)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' , Acad. Press (1986)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| − | Non-Archimedean norms satisfy | + | Non-Archimedean norms satisfy <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067360/n067360103.png" /> and hence do not satisfy the [[Archimedean axiom|Archimedean axiom]], whence the appellation. |
| − | and hence do not satisfy the [[Archimedean axiom|Archimedean axiom]], whence the appellation. | ||
Revision as of 14:52, 7 June 2020

A mapping  from
from  to the set
to the set  of real numbers, which satisfies the following conditions:
of real numbers, which satisfies the following conditions:
1)  , and
, and  if and only if
if and only if  ;
;
2)  ;
;
3)  .
.
Hence 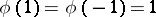 ;
; 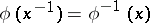 .
.
The norm of  is often denoted by
is often denoted by 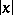 instead of
instead of 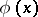 . A norm is also called an absolute value or a multiplicative valuation. Norms may (more generally) be considered on any ring with values in a linearly ordered ring [4]. See also Valuation.
. A norm is also called an absolute value or a multiplicative valuation. Norms may (more generally) be considered on any ring with values in a linearly ordered ring [4]. See also Valuation.
Examples of norms. If 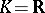 , the field of real numbers, then
, the field of real numbers, then 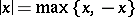 , the ordinary absolute value or modulus of the number
, the ordinary absolute value or modulus of the number 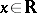 , is a norm. Similarly, if
, is a norm. Similarly, if 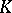 is the field
is the field  of complex numbers or the skew-field
of complex numbers or the skew-field  of quaternions, then
of quaternions, then 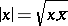 is a norm. The subfields of these fields are thus also provided with an induced norm. Any field has the trivial norm:
is a norm. The subfields of these fields are thus also provided with an induced norm. Any field has the trivial norm:
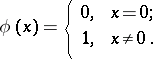 |
Finite fields and their algebraic extensions only have the trivial norm.
Examples of norms of another type are provided by logarithmic valuations of a field 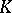 : If
: If  is a valuation on
is a valuation on 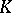 with values in the group
with values in the group  and if
and if  is a real number,
is a real number, 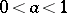 , then
, then 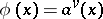 is a norm. For example, if
is a norm. For example, if 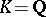 and
and  is the
is the 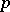 -adic valuation of the field
-adic valuation of the field  , then
, then  is called the
is called the 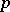 -adic absolute value or the
-adic absolute value or the 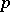 -adic norm. These absolute values satisfy the following condition, which is stronger than 3):
-adic norm. These absolute values satisfy the following condition, which is stronger than 3):
4) 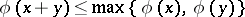 .
.
Norms satisfying condition 4) are known as ultra-metric norms or non-Archimedean norms (as distinct from Archimedean norms which do not satisfy this condition (but do satisfy 3)). They are distinguished by the fact that 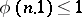 for all integers
for all integers  . All norms on a field of characteristic
. All norms on a field of characteristic 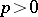 are ultra-metric. All ultra-metric norms are obtained from valuations as indicated above:
are ultra-metric. All ultra-metric norms are obtained from valuations as indicated above: 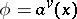 (and conversely,
(and conversely, 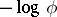 can always be taken as a valuation).
can always be taken as a valuation).
A norm 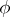 defines a metric on
defines a metric on 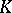 if
if 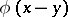 is taken as the distance between
is taken as the distance between  and
and 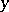 , and in this way it defines a topology on
, and in this way it defines a topology on  . The topology of any locally compact field is defined by some norm. Two norms
. The topology of any locally compact field is defined by some norm. Two norms  and
and 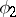 are said to be equivalent if they define the same topology; in a such case there exists a
are said to be equivalent if they define the same topology; in a such case there exists a  such that
such that  for all
for all 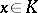 .
.
The structure of all Archimedean norms is given by Ostrowski's theorem: If 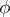 is an Archimedean norm on a field
is an Archimedean norm on a field 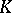 , then there exists an isomorphism of
, then there exists an isomorphism of 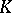 into a certain everywhere-dense subfield of one of the fields
into a certain everywhere-dense subfield of one of the fields 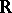 ,
, 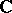 or
or  such that
such that 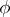 is equivalent to the norm induced by that of
is equivalent to the norm induced by that of 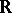 ,
, 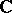 or
or  .
.
Any non-trivial norm of the field 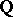 of rational numbers is equivalent either to a
of rational numbers is equivalent either to a 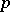 -adic norm
-adic norm 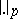 , where
, where  is a prime number, or to the ordinary norm. For any rational number
is a prime number, or to the ordinary norm. For any rational number 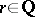 one has
one has
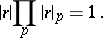 |
A similar formula is also valid for algebraic number fields [2], [3].
If 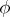 is a norm on a field
is a norm on a field 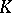 , then
, then 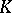 may be imbedded by the classical completion process in a field
may be imbedded by the classical completion process in a field 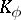 that is complete with respect to the norm that (uniquely) extends
that is complete with respect to the norm that (uniquely) extends  (cf. Complete topological space). One of the principal modern methods in the study of fields is the imbedding of a field
(cf. Complete topological space). One of the principal modern methods in the study of fields is the imbedding of a field 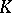 into the direct product
into the direct product 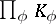 of all completions
of all completions 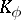 of the field
of the field 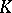 with respect to all non-trivial norms of
with respect to all non-trivial norms of  (see Adèle). If
(see Adèle). If 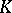 admits non-trivial valuations, then it is dense in
admits non-trivial valuations, then it is dense in 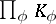 in the adèlic topology; in fact, if
in the adèlic topology; in fact, if 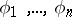 are non-trivial, non-equivalent norms on
are non-trivial, non-equivalent norms on 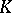 , if
, if  are elements of
are elements of 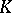 and if
and if 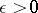 , then there exists an
, then there exists an 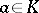 such that
such that 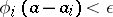 for all
for all 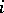 (the approximation theorem for norms).
(the approximation theorem for norms).
A norm on a field 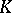 may be extended (in general, non-uniquely) to any algebraic field extension of the field
may be extended (in general, non-uniquely) to any algebraic field extension of the field 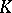 . If
. If  is complete with respect to the norm
is complete with respect to the norm 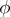 and if
and if 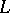 is an extension of
is an extension of  of degree
of degree  , the extension of
, the extension of 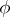 to
to 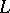 is unique, and is given by the formula
is unique, and is given by the formula
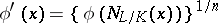 |
for 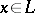 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [2] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [3] | S. Lang, "Algebra" , Addison-Wesley (1984) |
| [4] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [5] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
Comments
Non-Archimedean norms satisfy 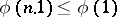 and hence do not satisfy the Archimedean axiom, whence the appellation.
and hence do not satisfy the Archimedean axiom, whence the appellation.
Norm on a field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Norm_on_a_field&oldid=49337