Difference between revisions of "Nehari extension problem"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 47954 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n1100101.png" /> be a given sequence of complex numbers. The Nehari extension problem is the problem to find (if possible) all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n1100102.png" /> satisfying the following conditions: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | if | ||
| − | |||
| − | + | i) the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n1100103.png" />th Fourier coefficient <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n1100104.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n1100105.png" /> is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n1100106.png" /> for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n1100107.png" />; | |
| − | |||
| − | + | ii) the norm constraint <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n1100108.png" /> holds true. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n1100109.png" /> is the norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001010.png" /> as an element of the Lebesgue function space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001012.png" /> is the unit circle. Instead of condition ii) one may require <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001013.png" />, and in the latter case one calls the problem suboptimal. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ii) the norm constraint | ||
| − | holds true. Here, | ||
| − | is the norm of | ||
| − | as an element of the Lebesgue function space | ||
| − | and | ||
| − | is the unit circle. Instead of condition ii) one may require | ||
| − | and in the latter case one calls the problem suboptimal. | ||
The Nehari extension problem is not always solvable. In fact (see [[#References|[a12]]]), the problem has a solution if and only if the infinite [[Hankel matrix]] | The Nehari extension problem is not always solvable. In fact (see [[#References|[a12]]]), the problem has a solution if and only if the infinite [[Hankel matrix]] | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001014.png" /></td> </tr></table> | |
| − | |||
| − | induces a bounded [[Linear operator|linear operator]] | + | induces a bounded [[Linear operator|linear operator]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001015.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001016.png" />, the [[Hilbert space|Hilbert space]] of all square-summable sequences, such that its operator norm is at most one, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001017.png" />. The suboptimal version of the problem is solvable if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001018.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001019.png" />, either the solution of the Nehari extension problem is unique or there are infinitely many solutions. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001020.png" />, then the problem and its suboptimal version always have infinitely many solutions, which can be parametrized by a fractional-linear mapping. |
| − | on | ||
| − | the [[Hilbert space|Hilbert space]] of all square-summable sequences, such that its operator norm is at most one, i.e., | ||
| − | The suboptimal version of the problem is solvable if and only if | ||
| − | If | ||
| − | either the solution of the Nehari extension problem is unique or there are infinitely many solutions. If | ||
| − | then the problem and its suboptimal version always have infinitely many solutions, which can be parametrized by a fractional-linear mapping. | ||
| − | For the suboptimal case, the set of all solutions | + | For the suboptimal case, the set of all solutions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001021.png" /> in the Wiener algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001022.png" />, i.e., when one requires additionally that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001023.png" />, can be described as follows. In this case, it is assumed that the given sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001024.png" /> is absolutely summable. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001025.png" />. Then the operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001027.png" /> are boundedly invertible on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001028.png" />, and one can build the following infinite column vectors: |
| − | in the Wiener algebra | ||
| − | i.e., when one requires additionally that | ||
| − | can be described as follows. In this case, it is assumed that the given sequence | ||
| − | is absolutely summable. Let | ||
| − | Then the operators | ||
| − | and | ||
| − | are boundedly invertible on | ||
| − | and one can build the following infinite column vectors: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001029.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001030.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001031.png" /></td> </tr></table> | |
| − | |||
Now, consider the functions | Now, consider the functions | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001032.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001033.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001034.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | Then, each solution | + | Then, each solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001035.png" /> of the suboptimal Nehari extension problem for the sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001036.png" /> is of the form |
| − | of the suboptimal Nehari extension problem for the sequence | ||
| − | is of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001037.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001038.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001039.png" /> is an arbitrary element of the Wiener algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001040.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001041.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001042.png" /> and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001043.png" />th Fourier coefficient of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001044.png" /> is zero for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001045.png" />. Moreover, (a1) gives a one-to-one correspondence between all such <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001046.png" /> and all solutions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001047.png" />. The central solution, i.e., the solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001048.png" />, which one obtains when the free parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001049.png" /> in (a1) is identically zero, has a maximum entropy characterization. In fact, it is the unique solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001050.png" /> of the suboptimal Nehari extension problem that maximizes the entropy integral |
| − | and | ||
| − | is an arbitrary element of the Wiener algebra | ||
| − | such that | ||
| − | for | ||
| − | and the | ||
| − | th Fourier coefficient of | ||
| − | is zero for each | ||
| − | Moreover, (a1) gives a one-to-one correspondence between all such | ||
| − | and all solutions | ||
| − | The central solution, i.e., the solution | ||
| − | which one obtains when the free parameter | ||
| − | in (a1) is identically zero, has a maximum entropy characterization. In fact, it is the unique solution | ||
| − | of the suboptimal Nehari extension problem that maximizes the entropy integral | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001051.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | The Nehari extension problem has natural generalizations for matrix-valued and operator-valued functions, and it has two-block and four-block analogues. In the matrix-valued case, a superoptimal Nehari extension problem is studied also. In the latter problem the constraint is made not only for the norm, but also for a number of first singular values [[#References|[a13]]]. There exist many different approaches to treat the Nehari problem and its various generalizations. For instance, the method of one-step extensions (see [[#References|[a1]]]), the commutant-lifting approach (see [[#References|[a6]]] and [[Commutant lifting theorem|Commutant lifting theorem]]), the [[Band method|band method]] (see [[#References|[a10]]]), reproducing-kernel Hilbert space techniques (see [[#References|[a5]]]), and Beurling–Lax methods in Krein spaces (see [[#References|[a4]]] and [[Krein space|Krein space]]). The results are used in [[H^infinity-control-theory| | + | The Nehari extension problem has natural generalizations for matrix-valued and operator-valued functions, and it has two-block and four-block analogues. In the matrix-valued case, a superoptimal Nehari extension problem is studied also. In the latter problem the constraint is made not only for the norm, but also for a number of first singular values [[#References|[a13]]]. There exist many different approaches to treat the Nehari problem and its various generalizations. For instance, the method of one-step extensions (see [[#References|[a1]]]), the commutant-lifting approach (see [[#References|[a6]]] and [[Commutant lifting theorem|Commutant lifting theorem]]), the [[Band method|band method]] (see [[#References|[a10]]]), reproducing-kernel Hilbert space techniques (see [[#References|[a5]]]), and Beurling–Lax methods in Krein spaces (see [[#References|[a4]]] and [[Krein space|Krein space]]). The results are used in [[H^infinity-control-theory|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001052.png" /> control theory]] (see [[#References|[a8]]]), and when the data are Fourier coefficients of a rational matrix function, the formulas for the coefficients in the linear fractional representation (a1) can be represented explicitly in state-space form (see [[#References|[a9]]] and [[#References|[a3]]]). |
| − | control theory]] (see [[#References|[a8]]]), and when the data are Fourier coefficients of a rational matrix function, the formulas for the coefficients in the linear fractional representation (a1) can be represented explicitly in state-space form (see [[#References|[a9]]] and [[#References|[a3]]]). | ||
The Nehari extension problem also has non-stationary versions, in which the role of analytic functions is taken over by lower-triangular matrices. An example is the problem to complete a given lower-triangular array of numbers, | The Nehari extension problem also has non-stationary versions, in which the role of analytic functions is taken over by lower-triangular matrices. An example is the problem to complete a given lower-triangular array of numbers, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001053.png" /></td> </tr></table> | |
| − | |||
| − | to a full infinite matrix such that the resulting operator on | + | to a full infinite matrix such that the resulting operator on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001054.png" /> is bounded and has operator norm at most one. The non-stationary variants of the Nehari extension problem have been treated in terms of nest algebras [[#References|[a2]]]. The main results for the stationary case carry over to the non-stationary case [[#References|[a11]]], [[#References|[a7]]]. |
| − | is bounded and has operator norm at most one. The non-stationary variants of the Nehari extension problem have been treated in terms of nest algebras [[#References|[a2]]]. The main results for the stationary case carry over to the non-stationary case [[#References|[a11]]], [[#References|[a7]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.M. Adamjan, D.Z. Arov, M.G. Krein, "Infinite Hankel block matrices and related extension problems" ''Transl. Amer. Math. Soc.'' , '''111''' (1978) pp. 133–156 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''6''' (1971) pp. 87–112</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.B. Arveson, "Interpolation in nest algebras" ''J. Funct. Anal.'' , '''20''' (1975) pp. 208–233</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Ball, I. Gohberg, L. Rodman, "Interpolation of rational matrix functions" , ''Operator Theory: Advances and Applications'' , '''45''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Ball, J.W. Helton, "A Beurling–Lax theorem for Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001055.png" /> which contains classical interpolation theory" ''J. Operator Th.'' , '''9''' (1983) pp. 107–142</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Dym, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001056.png" /> contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , ''CBMS'' , '''71''' , Amer. Math. Soc. (1989)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , ''Operator Theory: Advances and Applications'' , '''44''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> C. Foias, A.E. Frazho, I. Gohberg, M.A. Kaashoek, "Discrete time-variant interpolation as classical interpolation with an operator argument" ''Integral Eq. Operator Th.'' , '''26''' (1996) pp. 371–403</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> B.A. Francis, "A course in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001057.png" /> control theory" , Springer (1987)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> K. Glover, "All optimal Hankel-norm approximations of linear multivariable systems and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001058.png" />-error bounds" ''Int. J. Control'' , '''39''' (1984) pp. 1115–1193</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> I. Gohberg, S. Goldberg, M.A Kaashoek, "Classes of linear operators II" , ''Operator Theory: Advances and Applications'' , '''63''' , Birkhäuser (1993)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> I. Gohberg, M.A. Kaashoek, H.J. Woerdeman, "The band method for positive and contractive extension problems: An alternative version and new applications" ''Integral Eq. Operator Th.'' , '''12''' (1989) pp. 343–382</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> Z. Nehari, "On bounded bilinear forms" ''Ann. of Math.'' , '''65''' (1957) pp. 153–162</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> V.V. Peller, N.J. Young, "Superoptimal analytic approximations of matrix functions" ''J. Funct. Anal.'' , '''120''' (1994) pp. 300–343</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.M. Adamjan, D.Z. Arov, M.G. Krein, "Infinite Hankel block matrices and related extension problems" ''Transl. Amer. Math. Soc.'' , '''111''' (1978) pp. 133–156 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''6''' (1971) pp. 87–112</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.B. Arveson, "Interpolation in nest algebras" ''J. Funct. Anal.'' , '''20''' (1975) pp. 208–233</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Ball, I. Gohberg, L. Rodman, "Interpolation of rational matrix functions" , ''Operator Theory: Advances and Applications'' , '''45''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Ball, J.W. Helton, "A Beurling–Lax theorem for Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001055.png" /> which contains classical interpolation theory" ''J. Operator Th.'' , '''9''' (1983) pp. 107–142</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Dym, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001056.png" /> contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , ''CBMS'' , '''71''' , Amer. Math. Soc. (1989)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , ''Operator Theory: Advances and Applications'' , '''44''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> C. Foias, A.E. Frazho, I. Gohberg, M.A. Kaashoek, "Discrete time-variant interpolation as classical interpolation with an operator argument" ''Integral Eq. Operator Th.'' , '''26''' (1996) pp. 371–403</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> B.A. Francis, "A course in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001057.png" /> control theory" , Springer (1987)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> K. Glover, "All optimal Hankel-norm approximations of linear multivariable systems and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001058.png" />-error bounds" ''Int. J. Control'' , '''39''' (1984) pp. 1115–1193</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> I. Gohberg, S. Goldberg, M.A Kaashoek, "Classes of linear operators II" , ''Operator Theory: Advances and Applications'' , '''63''' , Birkhäuser (1993)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> I. Gohberg, M.A. Kaashoek, H.J. Woerdeman, "The band method for positive and contractive extension problems: An alternative version and new applications" ''Integral Eq. Operator Th.'' , '''12''' (1989) pp. 343–382</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> Z. Nehari, "On bounded bilinear forms" ''Ann. of Math.'' , '''65''' (1957) pp. 153–162</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> V.V. Peller, N.J. Young, "Superoptimal analytic approximations of matrix functions" ''J. Funct. Anal.'' , '''120''' (1994) pp. 300–343</TD></TR></table> | ||
Revision as of 14:32, 7 June 2020
Let 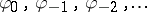 be a given sequence of complex numbers. The Nehari extension problem is the problem to find (if possible) all
be a given sequence of complex numbers. The Nehari extension problem is the problem to find (if possible) all 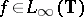 satisfying the following conditions:
satisfying the following conditions:
i) the  th Fourier coefficient
th Fourier coefficient 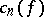 of
of 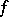 is equal to
is equal to 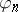 for each
for each 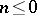 ;
;
ii) the norm constraint 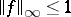 holds true. Here,
holds true. Here, 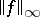 is the norm of
is the norm of 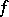 as an element of the Lebesgue function space
as an element of the Lebesgue function space 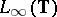 and
and 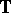 is the unit circle. Instead of condition ii) one may require
is the unit circle. Instead of condition ii) one may require 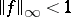 , and in the latter case one calls the problem suboptimal.
, and in the latter case one calls the problem suboptimal.
The Nehari extension problem is not always solvable. In fact (see [a12]), the problem has a solution if and only if the infinite Hankel matrix
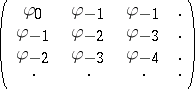 |
induces a bounded linear operator 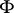 on
on 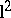 , the Hilbert space of all square-summable sequences, such that its operator norm is at most one, i.e.,
, the Hilbert space of all square-summable sequences, such that its operator norm is at most one, i.e.,  . The suboptimal version of the problem is solvable if and only if
. The suboptimal version of the problem is solvable if and only if 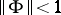 . If
. If 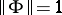 , either the solution of the Nehari extension problem is unique or there are infinitely many solutions. If
, either the solution of the Nehari extension problem is unique or there are infinitely many solutions. If 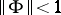 , then the problem and its suboptimal version always have infinitely many solutions, which can be parametrized by a fractional-linear mapping.
, then the problem and its suboptimal version always have infinitely many solutions, which can be parametrized by a fractional-linear mapping.
For the suboptimal case, the set of all solutions 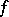 in the Wiener algebra
in the Wiener algebra 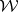 , i.e., when one requires additionally that
, i.e., when one requires additionally that 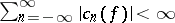 , can be described as follows. In this case, it is assumed that the given sequence
, can be described as follows. In this case, it is assumed that the given sequence 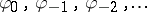 is absolutely summable. Let
is absolutely summable. Let 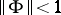 . Then the operators
. Then the operators 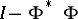 and
and 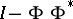 are boundedly invertible on
are boundedly invertible on  , and one can build the following infinite column vectors:
, and one can build the following infinite column vectors:
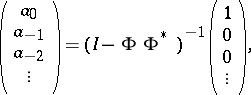 |
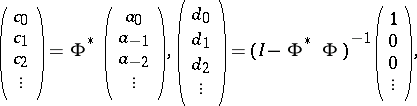 |
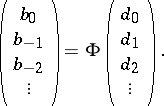 |
Now, consider the functions
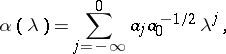 |
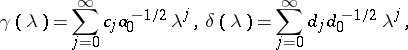 |
 |
Then, each solution 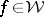 of the suboptimal Nehari extension problem for the sequence
of the suboptimal Nehari extension problem for the sequence  is of the form
is of the form
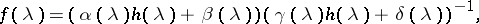 | (a1) |
where 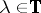 and
and 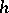 is an arbitrary element of the Wiener algebra
is an arbitrary element of the Wiener algebra 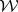 such that
such that 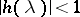 for
for 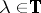 and the
and the  th Fourier coefficient of
th Fourier coefficient of 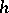 is zero for each
is zero for each 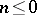 . Moreover, (a1) gives a one-to-one correspondence between all such
. Moreover, (a1) gives a one-to-one correspondence between all such 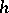 and all solutions
and all solutions 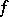 . The central solution, i.e., the solution
. The central solution, i.e., the solution 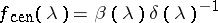 , which one obtains when the free parameter
, which one obtains when the free parameter  in (a1) is identically zero, has a maximum entropy characterization. In fact, it is the unique solution
in (a1) is identically zero, has a maximum entropy characterization. In fact, it is the unique solution 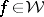 of the suboptimal Nehari extension problem that maximizes the entropy integral
of the suboptimal Nehari extension problem that maximizes the entropy integral
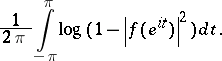 |
The Nehari extension problem has natural generalizations for matrix-valued and operator-valued functions, and it has two-block and four-block analogues. In the matrix-valued case, a superoptimal Nehari extension problem is studied also. In the latter problem the constraint is made not only for the norm, but also for a number of first singular values [a13]. There exist many different approaches to treat the Nehari problem and its various generalizations. For instance, the method of one-step extensions (see [a1]), the commutant-lifting approach (see [a6] and Commutant lifting theorem), the band method (see [a10]), reproducing-kernel Hilbert space techniques (see [a5]), and Beurling–Lax methods in Krein spaces (see [a4] and Krein space). The results are used in 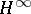 control theory (see [a8]), and when the data are Fourier coefficients of a rational matrix function, the formulas for the coefficients in the linear fractional representation (a1) can be represented explicitly in state-space form (see [a9] and [a3]).
control theory (see [a8]), and when the data are Fourier coefficients of a rational matrix function, the formulas for the coefficients in the linear fractional representation (a1) can be represented explicitly in state-space form (see [a9] and [a3]).
The Nehari extension problem also has non-stationary versions, in which the role of analytic functions is taken over by lower-triangular matrices. An example is the problem to complete a given lower-triangular array of numbers,
 |
to a full infinite matrix such that the resulting operator on 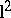 is bounded and has operator norm at most one. The non-stationary variants of the Nehari extension problem have been treated in terms of nest algebras [a2]. The main results for the stationary case carry over to the non-stationary case [a11], [a7].
is bounded and has operator norm at most one. The non-stationary variants of the Nehari extension problem have been treated in terms of nest algebras [a2]. The main results for the stationary case carry over to the non-stationary case [a11], [a7].
References
| [a1] | V.M. Adamjan, D.Z. Arov, M.G. Krein, "Infinite Hankel block matrices and related extension problems" Transl. Amer. Math. Soc. , 111 (1978) pp. 133–156 Izv. Akad. Nauk SSSR Ser. Mat. , 6 (1971) pp. 87–112 |
| [a2] | W.B. Arveson, "Interpolation in nest algebras" J. Funct. Anal. , 20 (1975) pp. 208–233 |
| [a3] | J. Ball, I. Gohberg, L. Rodman, "Interpolation of rational matrix functions" , Operator Theory: Advances and Applications , 45 , Birkhäuser (1990) |
| [a4] | J. Ball, J.W. Helton, "A Beurling–Lax theorem for Lie group 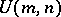 which contains classical interpolation theory" J. Operator Th. , 9 (1983) pp. 107–142 which contains classical interpolation theory" J. Operator Th. , 9 (1983) pp. 107–142 |
| [a5] | H. Dym, "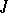 contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , CBMS , 71 , Amer. Math. Soc. (1989) contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , CBMS , 71 , Amer. Math. Soc. (1989) |
| [a6] | C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , Operator Theory: Advances and Applications , 44 , Birkhäuser (1990) |
| [a7] | C. Foias, A.E. Frazho, I. Gohberg, M.A. Kaashoek, "Discrete time-variant interpolation as classical interpolation with an operator argument" Integral Eq. Operator Th. , 26 (1996) pp. 371–403 |
| [a8] | B.A. Francis, "A course in 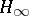 control theory" , Springer (1987) control theory" , Springer (1987) |
| [a9] | K. Glover, "All optimal Hankel-norm approximations of linear multivariable systems and the 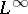 -error bounds" Int. J. Control , 39 (1984) pp. 1115–1193 -error bounds" Int. J. Control , 39 (1984) pp. 1115–1193 |
| [a10] | I. Gohberg, S. Goldberg, M.A Kaashoek, "Classes of linear operators II" , Operator Theory: Advances and Applications , 63 , Birkhäuser (1993) |
| [a11] | I. Gohberg, M.A. Kaashoek, H.J. Woerdeman, "The band method for positive and contractive extension problems: An alternative version and new applications" Integral Eq. Operator Th. , 12 (1989) pp. 343–382 |
| [a12] | Z. Nehari, "On bounded bilinear forms" Ann. of Math. , 65 (1957) pp. 153–162 |
| [a13] | V.V. Peller, N.J. Young, "Superoptimal analytic approximations of matrix functions" J. Funct. Anal. , 120 (1994) pp. 300–343 |
Nehari extension problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nehari_extension_problem&oldid=49318